Denoise
노이즈를 제거하는 과정을 denoise라고 하는데 우선 noise에 대서 알아보자. 다양한 노이즈의 종류가 있지만 대표적인 노이즈들을 한번 살펴보자.
Salt-and-pepper noise: 흑백 픽셀의 무작위 발생이다.
Impuse noise: 백색 픽셀의 무작위 발생이다.
Gaussian noise: 가우시안 정규분포를 따르는 노이즈로 자연발생한 노이즈들이 자연적인 분포를 따르며 발생하는 노이즈이다.

Gaussian noise를 Gaussian filter로 denoising하면 아래와 같이 standard한 denoising과정이 진행된다.

그러나 아래와 같은 Salt-and-pepper noise를 gaussian filter로 denoise를 하려하면 잘 진행이 되지 않는다. 다양한 사이즈의 필터를 이용해봤지만 그렇다할 개선사항이 보이지 않는다.

Order-statistics filter의 일종인 Median filter를 이용하면 이러한 문제를 해결할 수 있다. Median filter는 아래와 같이 본인을 포함한 window내의 모든 숫자중 중앙값을 자신의 값으로 대체하는 방식이다.



Gaussian filter와 다르게 median filter는 급격한 변화를 잘 보존하는 bilateral filter와 같이 edge preserve smoothing이라고 볼 수 있다. 예를 들어 흰색에서 검정사이의 경계선 부근이라고 생각해보면 filter가 통과하는 중에 흰색이 51%이상이면 흰색으로 판정되다가 검정색이 51%인 곳으로 넘어가는 순간 검정으로 판정된다. 둘을 적당히 섞어서 회색이 되는 일이 없는 것이다.
Edge Detection
픽셀의 2D 배열로부터 곡선 또는 윤곽선 세트로 영상을 매핑하는 과정을 Edge Detection이라고 한다. 물론 아래 그림처럼 그냥 물체의 경계를 딴다고 생각하면 간단하다.

Edge로 판단되게 만드는 요인은 아래와 같이 다양하다.

Edge를 정량적으로 판단하자면 영상 Intesity function의 급격한 변화가 있는 곳이다.
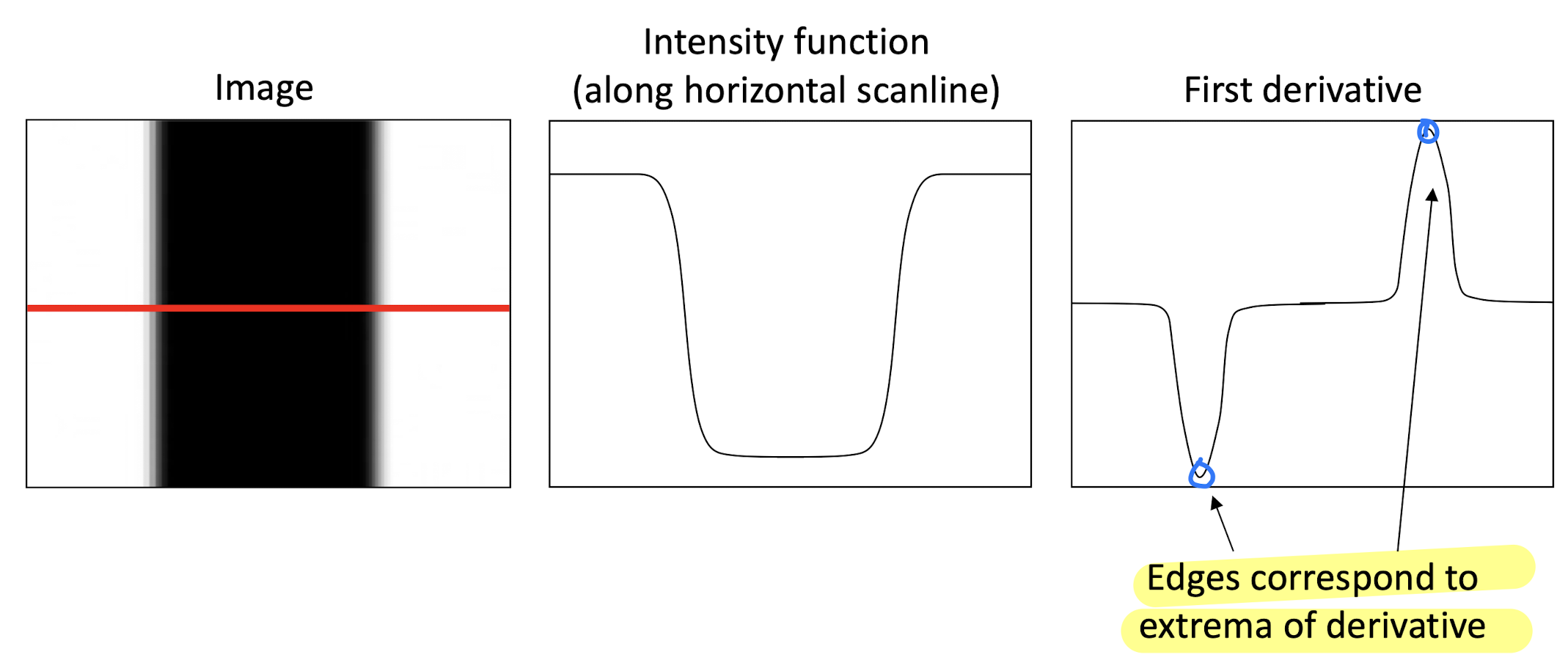
위 그림에서 볼 수 있듯이 Intensity function의 First derivative의 local minimum 지점들을 찾으면 edge를 쉽게 찾을 수 있다. 이때 First derivative는 그냥 한번 미분한 식이다.
2차함수에서 미분을 함수의 극한으로 표현하면 아래와 같다.
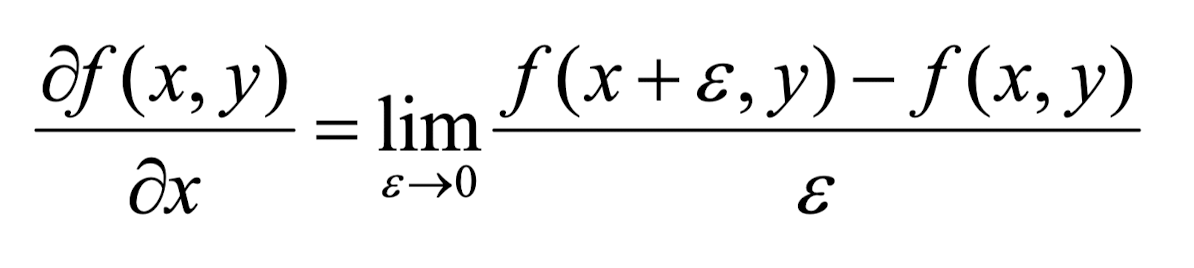
해당식을 2D 이미지에서 생각하면 최소단위가 한 픽셀이기 때문에 아래와 같이 epsilon의 최소값이 1이 된다는 것을 알 수 있다.
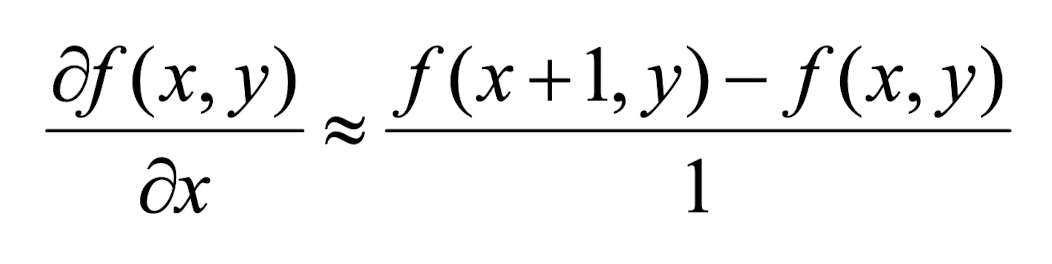

위 그림을 보면 왼쪽의 경우 가로로 -1,1필터를 이용하여 f(x+1,y)-f(x,y)를 만든 것이고 오른쪽의 경우 세로로 -1,1필터를 이용하여 f(x,y+1)-f(x,y)를 구현하여 미분값을 표현한것이다.
이미지에서 gradient는 아래와 같이 2차원이다. 이때 gradient는 jacobian의 특이한 case, 함수가 하나인 case를 의미한다는 것을 참고로 알아두자.
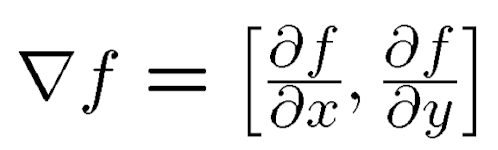
Gradient 계산 결과는 vector인데 이는 밝기 변화 방향을 뜻한다.
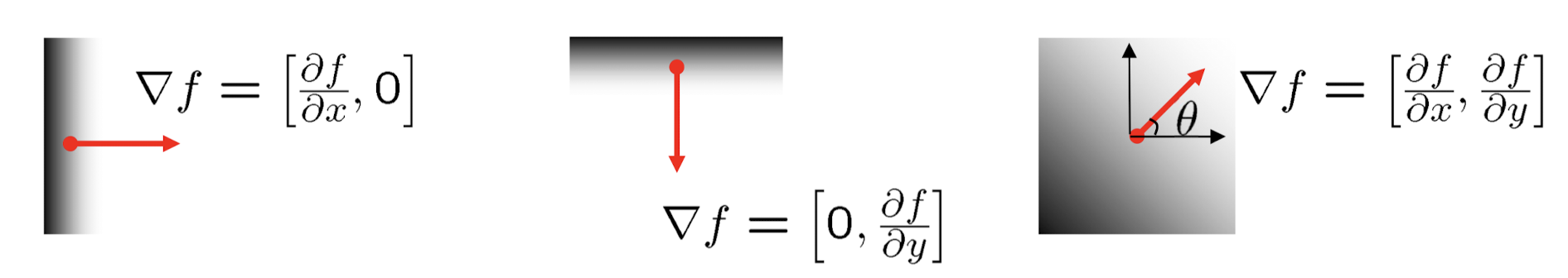
Gradient 방향의 각도는 아래와 같이 표현한다.
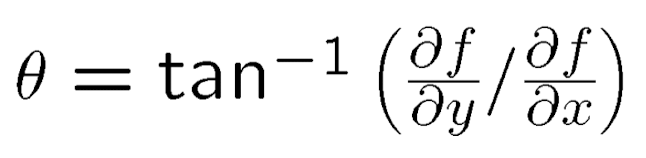
#include <math.h>
double atan2(double y, double x);프로그래밍 언어로는 atan2라는 함수를 이용해서 y/x의 역탄젠트를 구한다. 또한 edge의 강도는 아래와 같은 gradient magnitude로 계산할 수 있다.
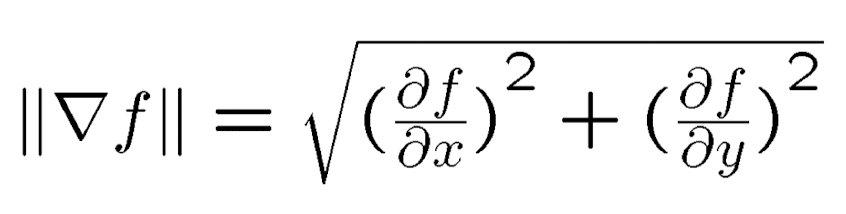
위에서본 호랑이 edge의 강도가 쎄지면 아래와 같이 될 것이다.

'Quality control (Univ. Study) > Digital Image Processing' 카테고리의 다른 글
| Digital Image Processing - Smoothing / Edging (0) | 2024.04.05 |
|---|---|
| DIP 실습 - SpreadSalt Noise / Gradation / Editing (0) | 2024.04.03 |
| Digital Image Processing - Filtering in Spatial Domain (0) | 2024.03.29 |
| Digital Image Processing - Pixel Processing / 히스토그램 (1) | 2024.03.26 |
| Digital Image Processing - 기본지식(2) (0) | 2024.03.22 |



