Pixel processing example
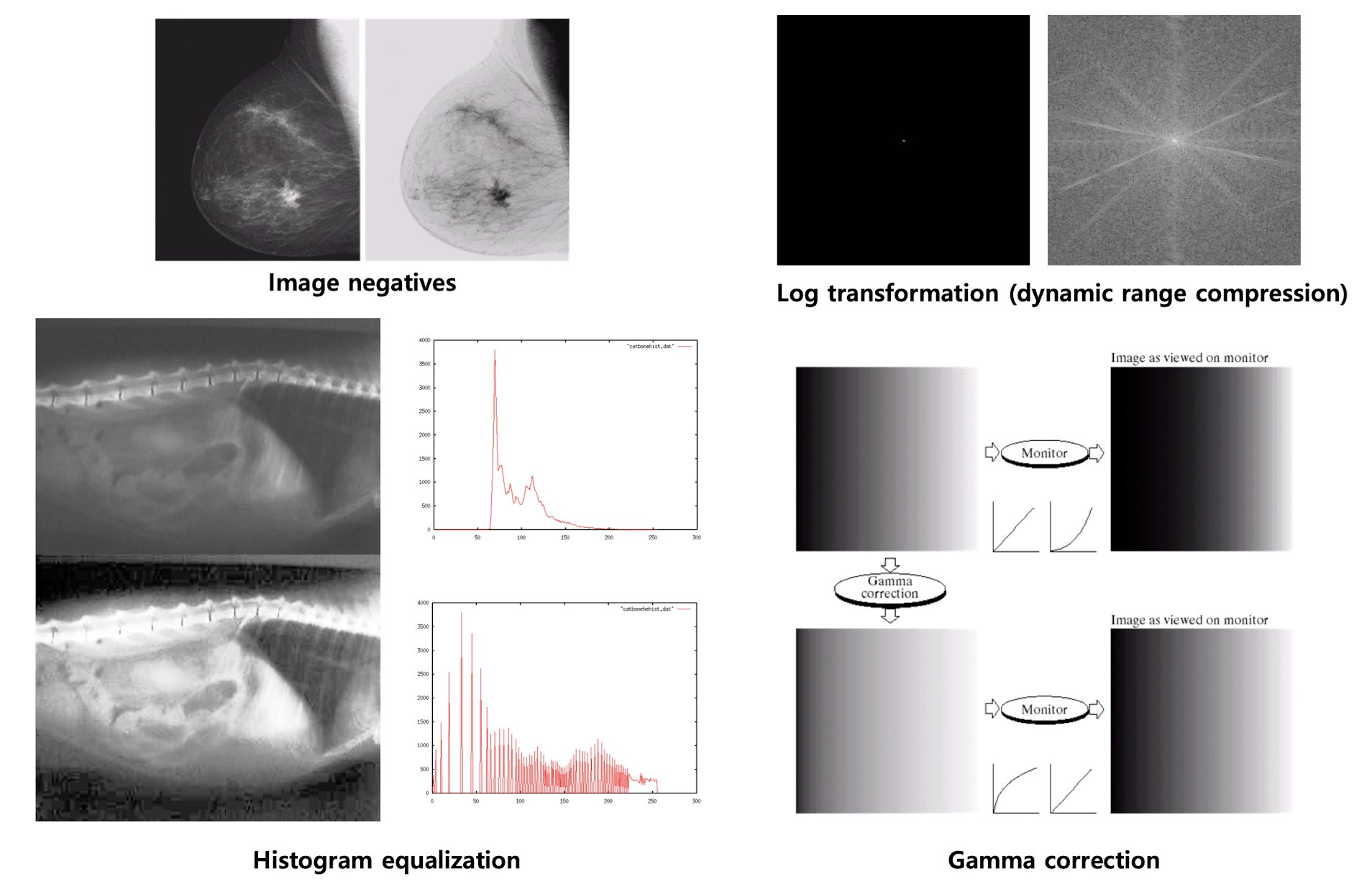
Image negatives: 픽셀 값을 최대값에서 뺀다. 밝은 영역이 어둡게, 어두운 영역이 밝게 변한다.
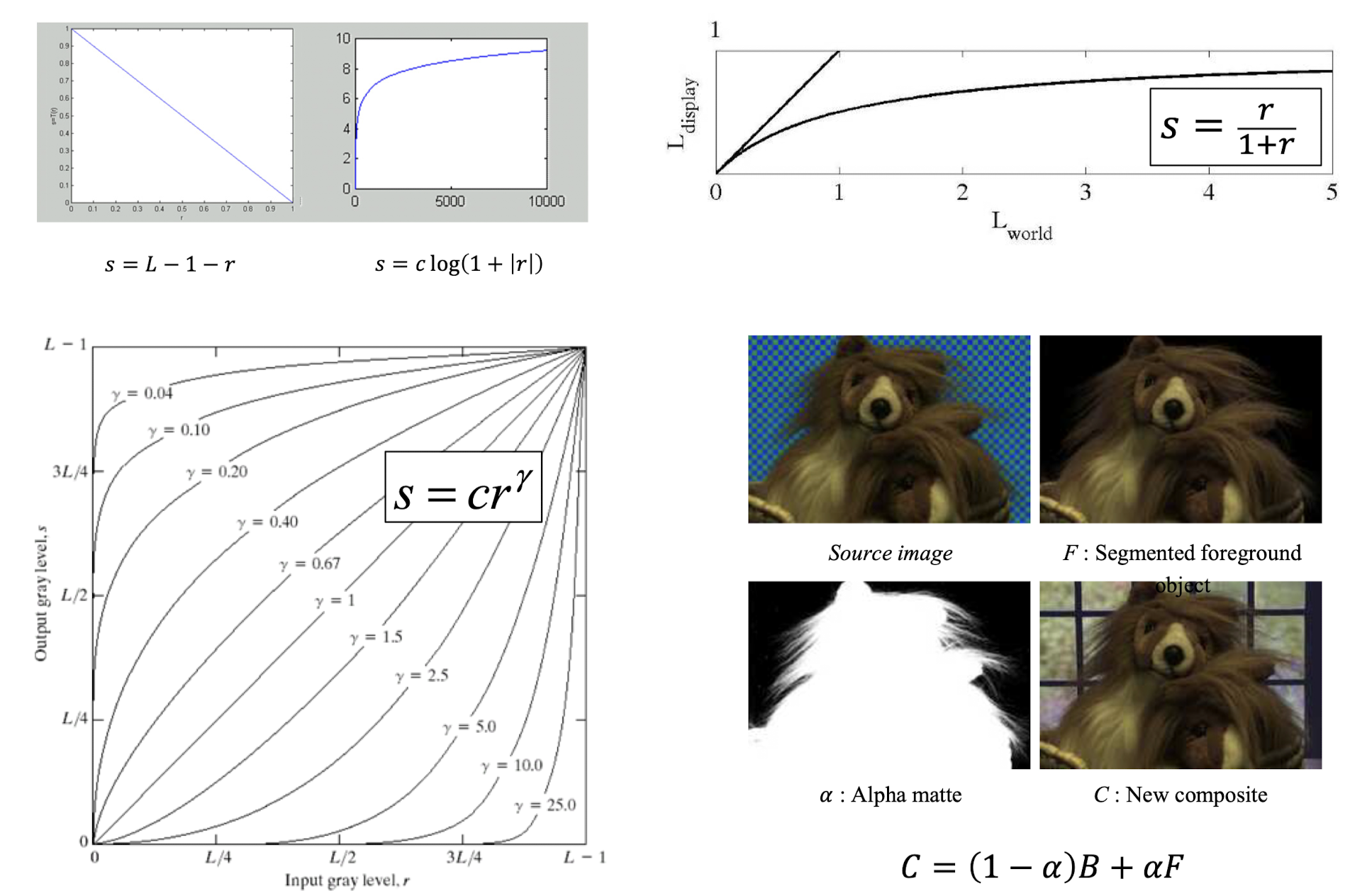
공식:s = T(r) = L-1-r
Log transform: 픽셀 값을 로그 함수에 적용한다. 어두운 영역의 명암 대비가 증가하고 밝은 영역은 덜 변한다.
공식: s = T(r) = clog(1+r)
Contrast Stretching: 픽셀 값을 일정한 범위에 매핑하여 명암 대비를 조절한다. 어두운 영역을 더 어둡게, 밝은 영역을 더 밝게 만들 수 있다.
Color transform: 색조, 채도, 명도를 조절하여 영상의 색상을 변환한다. 다양한 색상 효과를 만들 수 있다.
Gamma correction: 영상의 밝기 비선형성을 보정한다. 어둡거나 밝은 영상을 보다 자연스럽게 만들 수 있다.
공식: s = cr
Blending of two images: 두 이미지를 합성하여 새로운 이미지를 만든다. 투명도, 알파 채널 등을 사용하여 다양한 합성 효과를 만들 수 있다.
공식: C = (1 - a)B + aF

원본에서 좌상단의 그래프와 같이 필터를 적용하여 좌하단처럼 좀더 극단적으로 표현할 수 있고 우하단처럼 아예 Threshold를 정해두고 white, black으로 만들어 버릴 수도 있다.
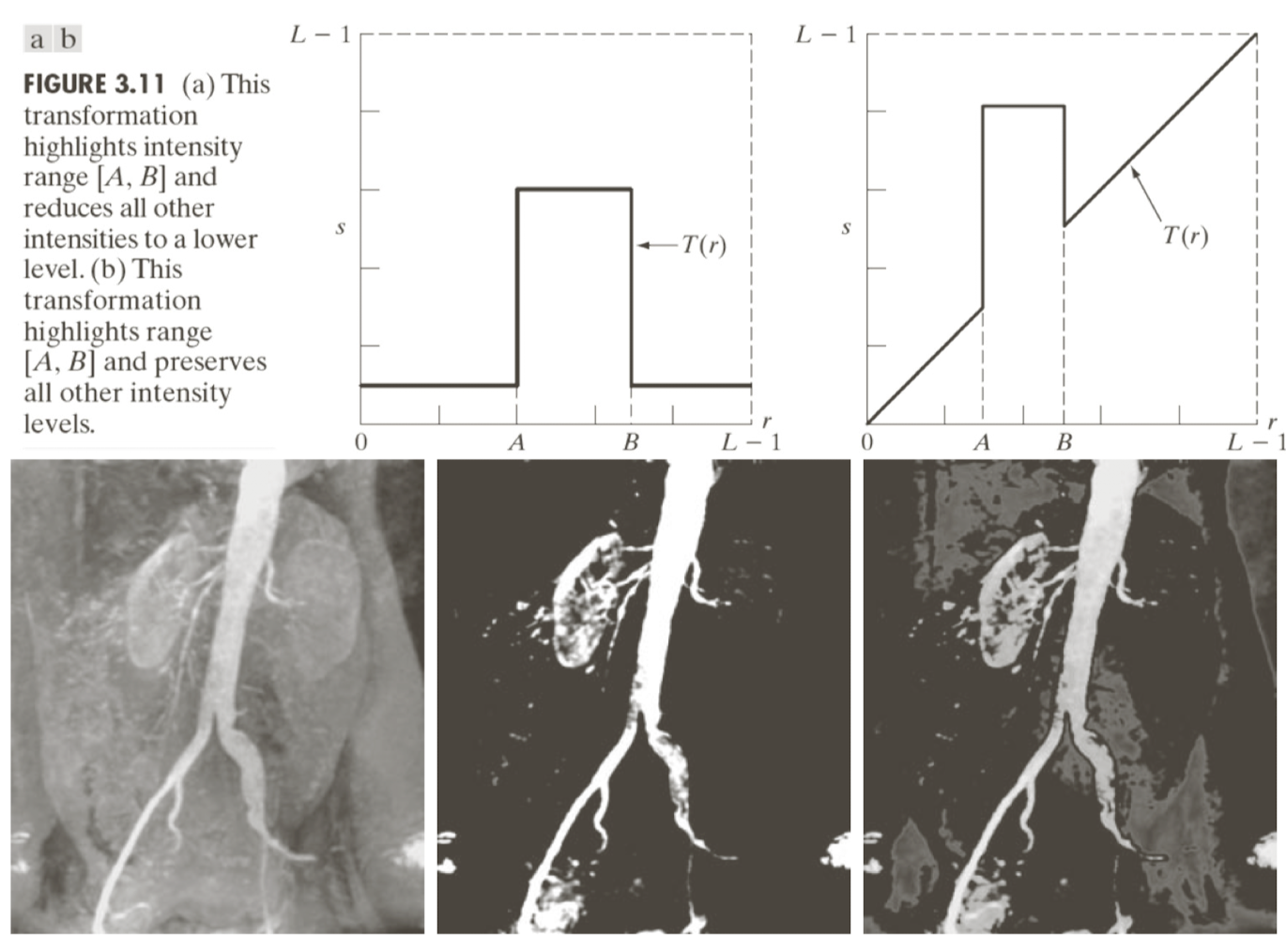
위는 Gray-Level slicing으로 A가 원본일때 B와 같이 강조하고 싶은 부분을 제외하고 전부 검정으로 만들어버릴 수도 있고 C처럼 나머지는 그대로 두고 강조하고 싶은 부분의 값을 늘리는 방식의 filter를 이용할 수도 있다.
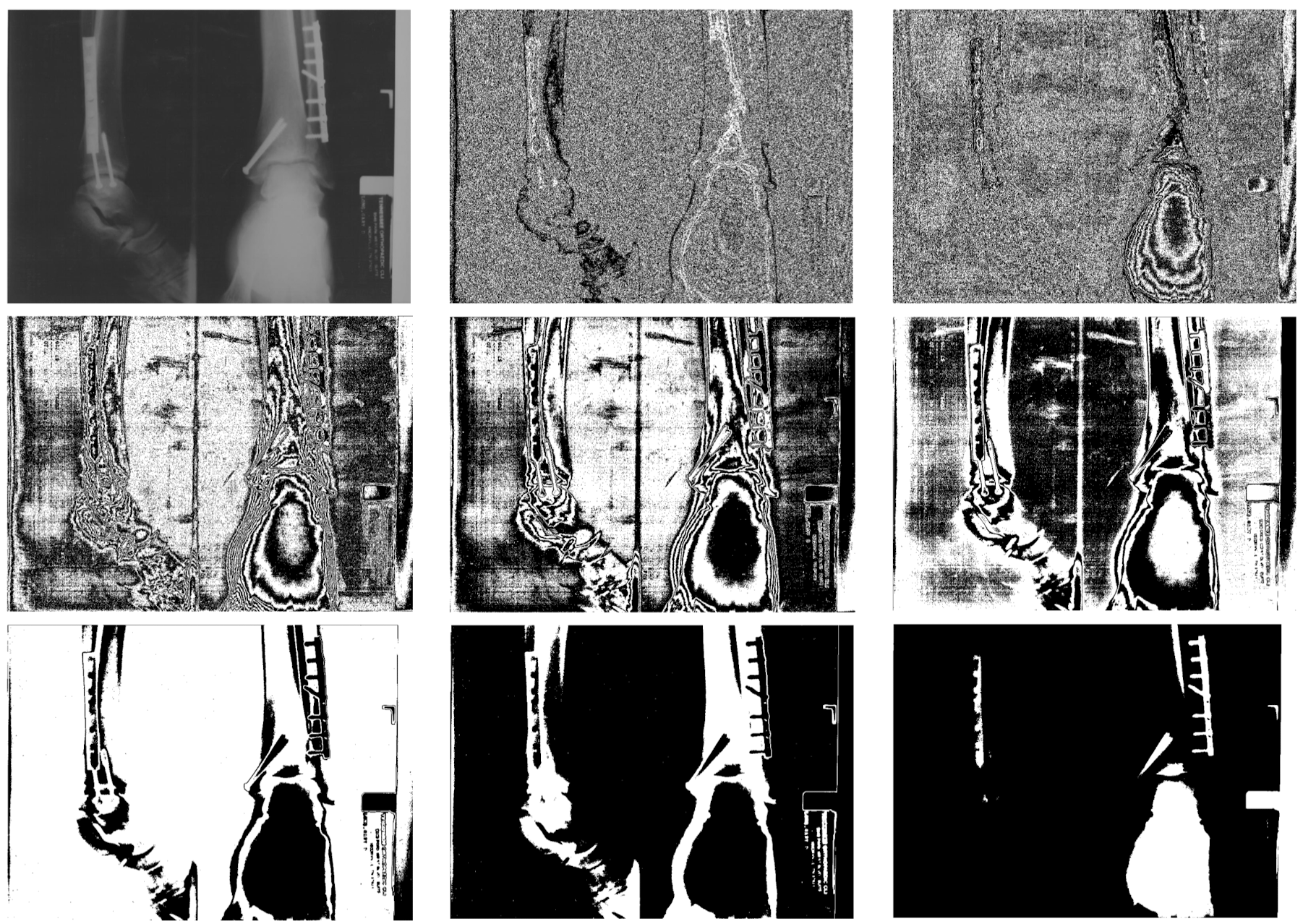
위는 Bit-Plane Slicing방식으로 8비트 값들중 하나씩 선택하여 기준으로 잡고 표현한 것이다. 이를 숫자를 통해 살펴보면 첫번째 사진이 원본이고 두번째 사진이 첫번째 비트를 기준으로 잡은 것이다. 11111110, 10101010, 11001110...등과 같이 첫번째 비트가 0인 부분은 무조건 00000000으로 표현한다. 반대로 첫번째 비트가 1이면 무조건 11111111으로 표현하다. 그래서 원본에서는 아주 가까운 밝기의 값이 정반대 값으로 분류되어 자글자글한 결과가 출력된다. 밑에쪽의 사진들을 살펴보면 중앙의 사진은 앞에서 두번째 비트를 기준으로 잡은 것이다. 예를 들어 11111110, 11101010, 11001110, 0110000... 등의 값들은 전부 11111111로 판단되고 그 반대의 경우 00000000으로 판단되어 10XXXXXX류의 모든 밝기 값이 하나로 통일되고 11XXXXXX류의 모든 밝기 값이 하나로 통일되기 때문에 고주파의 사진이 아니라 단순한 사진이 나오는 것을 볼 수 있다.
Histogram
Gray-level histogram은 이미지에서 각 회색 레벨에 대해 해당 레벨을 가지는 픽셀의 개수를 보여주는 함수이다.

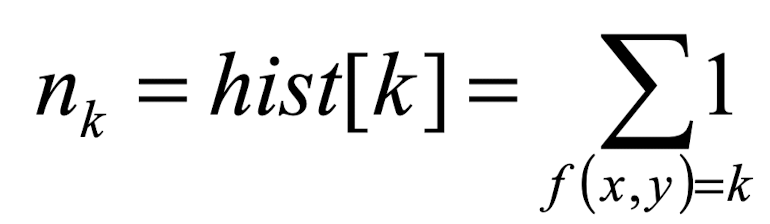
정규화된 히스토그램은 픽셀의 개수로 표현하는 것이 아니라 픽셀의 비율로 표현하기 때문에 크기가 다른 그림도 비교하기 유리하다.
예를 들어 10x10 크기의 이미지에서 gray scale 0에 해당하는 픽셀이 40개, gray scale 1에 해당하는 픽셀이 60개 있다고 가정하자. 일반적인 히스토그램 값은 0에 해당하는 막대 높이가 40, 1에 해당하는 막대 높이가 60이다. 정규화된 히스토그램 값은 0에 해당하는 막대 높이가 0.4 (40/100), 1에 해당하는 막대 높이가 0.6 (60/100)이다. 이는 다시말해 pdf로 표현하는 과정이라고 보면 된다.
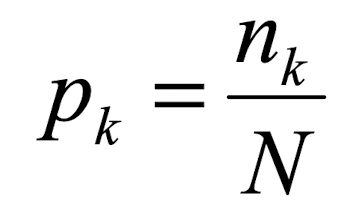
Histogram Equalization
히스토그램 평활화는 아래와 같이 편향된 밝기 값을 갖고 있는 사진을 보기 편하게 만드는 효과가 있다.
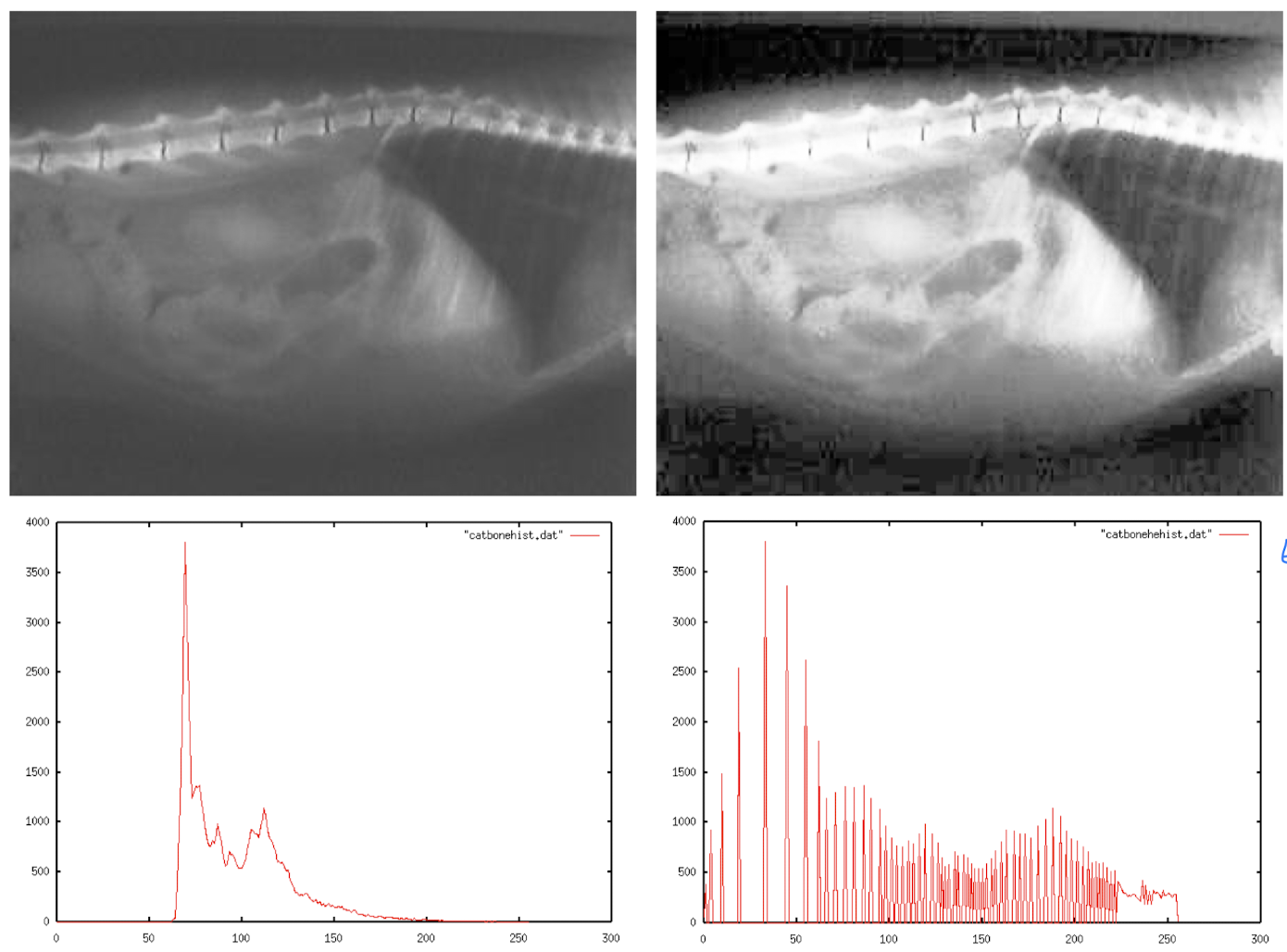
위 방식은 단순히 선형적으로 양쪽으로 당기는 방식을 이용한 것이다.
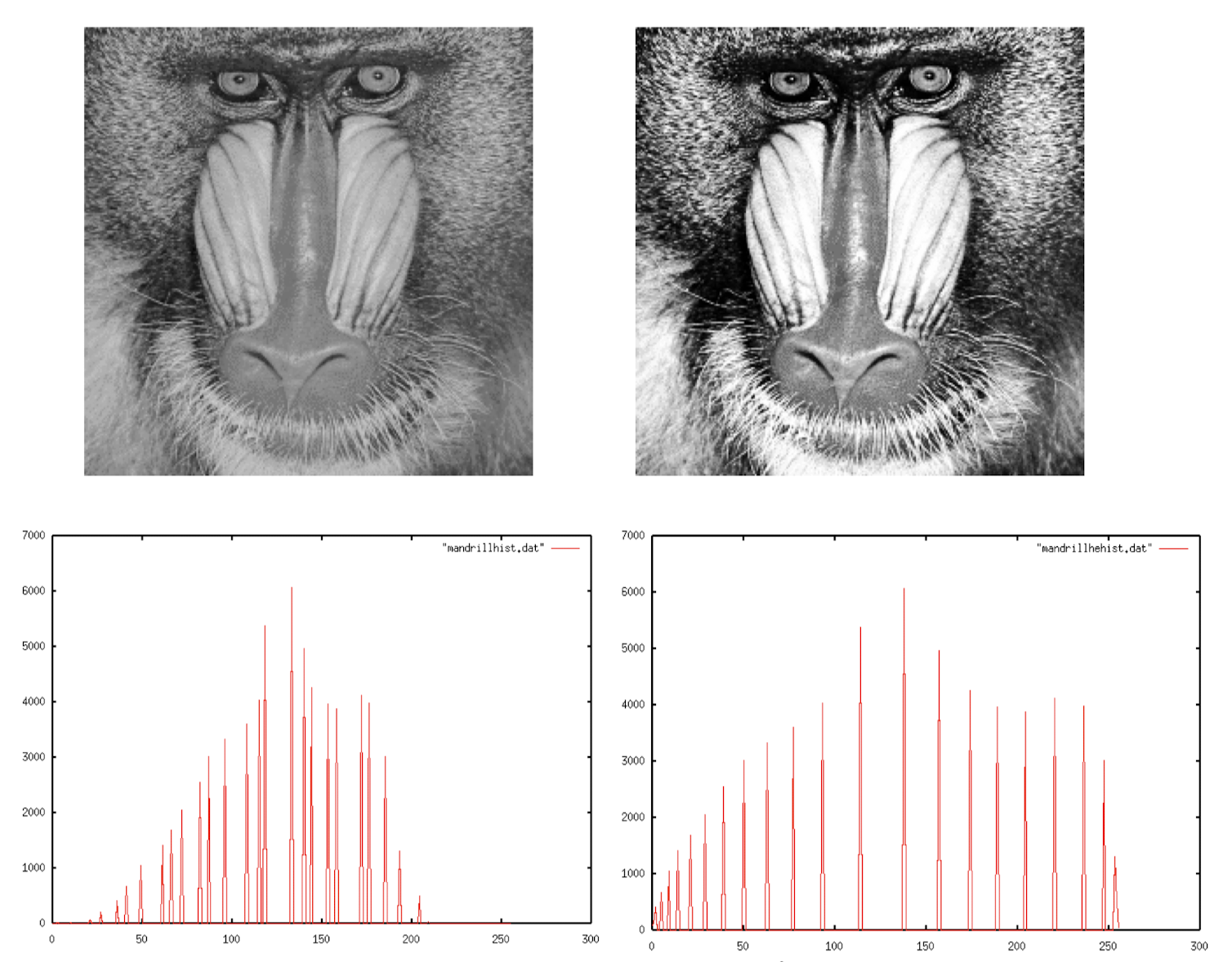
위 방식은 분포를 활용한 좀더 평활화를 잘 시킬 수 있는 방식이다.
분포를 활용한 평활화 방식의 방법에 대해서 살펴보자.
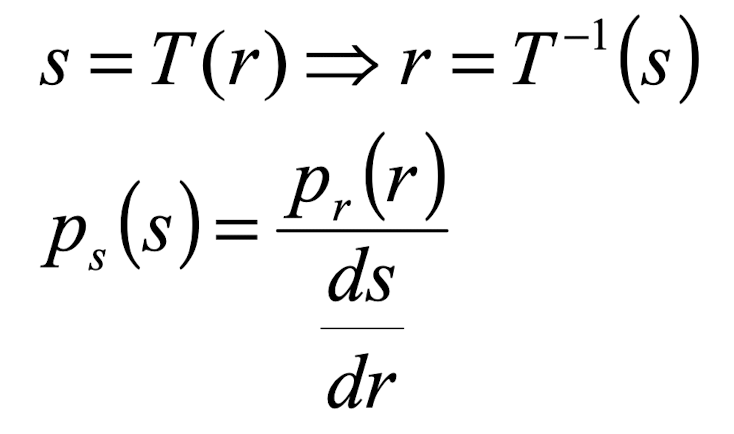
이 식은 확률변수의 변환에 의한 확률밀도함수의 변화 공식이다. 이를 단순한 히스토그램에서 예를 들어 살펴보자.
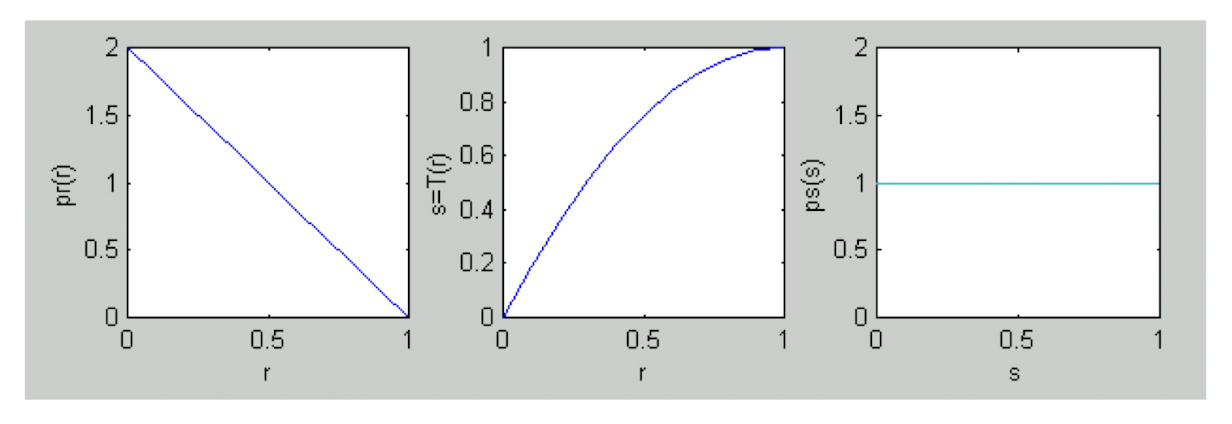
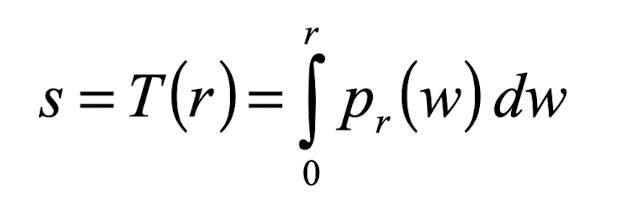
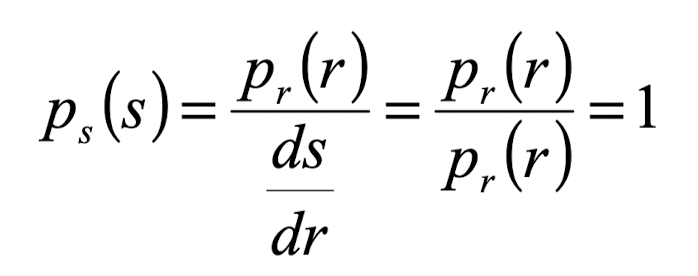
실수 범위인 경우 이론상 완전히 평활화 된다는 뜻이다.
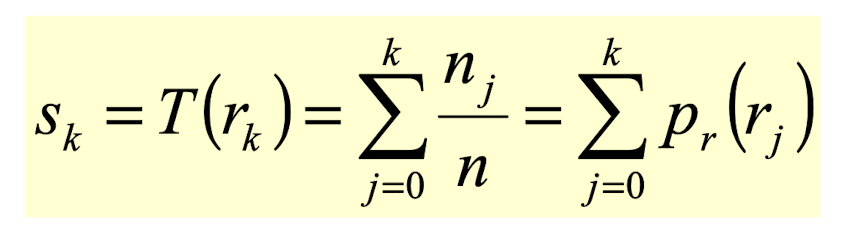
히스토그램 x축 화소값 및 도수의 변환 방식들이다.
3-bit 이미지에서 평활화 과정을 예시를 통해 살펴보자.
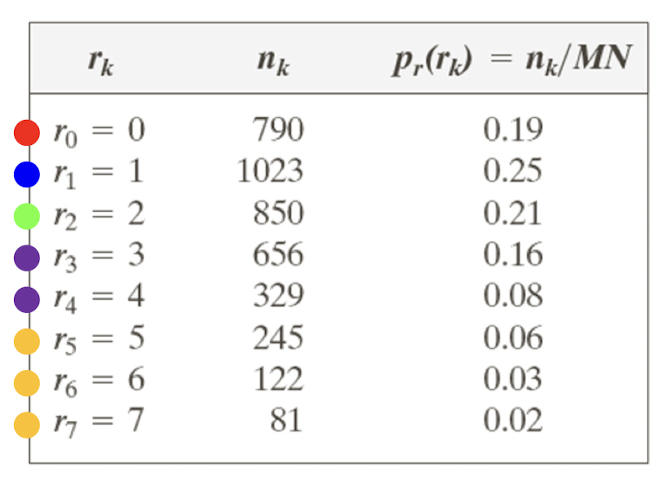

식에 따라 변환하면 위와 같이 변환된다.
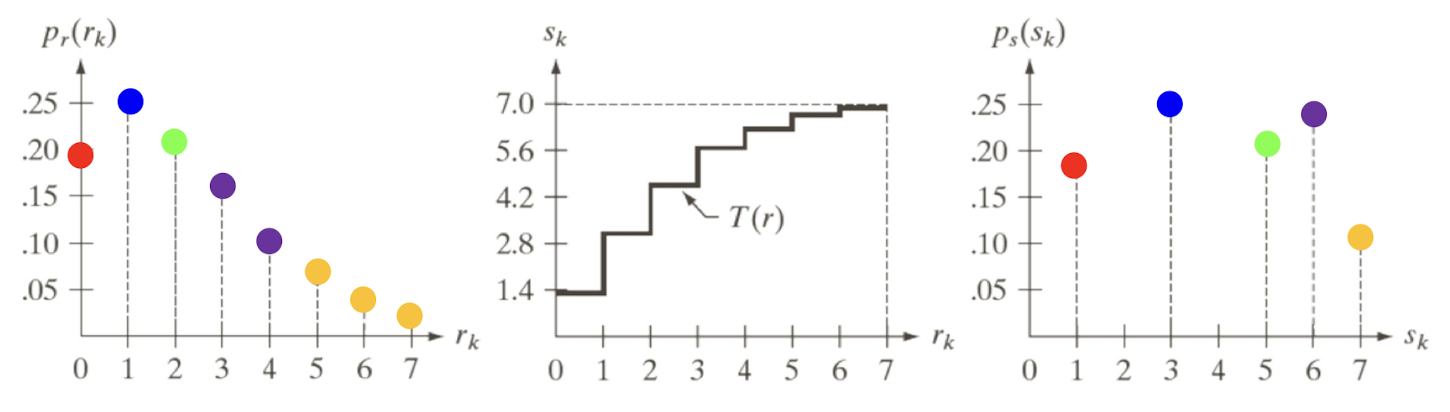
정성적으로 살펴보면 동일한 간격으로 있던 값들을 일정한 범위로 묶어서 숫자가 적은 값들은 하나로 통일하여 비슷하게 나눠갖도록하고 많이 나타난 값은 넓은 범위를 차지하도록하여 그 밀집도를 표현한다.
'Univ. Study > Digital Image Processing' 카테고리의 다른 글
| Digital Image Processing - Denoising / Filter / Edge Detection (1) | 2024.04.03 |
|---|---|
| Digital Image Processing - Filtering in Spatial Domain (0) | 2024.03.29 |
| Digital Image Processing - 기본지식(2) (1) | 2024.03.22 |
| Digital Image Processing - 기본 지식(1) (0) | 2024.03.17 |
| Digital Image Processing - Intro (1) | 2024.03.13 |



