Noise
Signal에서 변화를 감지하려면 미분을 해서 찾아내야 하는데 미분은 noise에 굉장히 취약하다. 미분을 하면 기울기가 나오는데 아무리 작은 noise라도 위아래로 피크가 생기면 그 기울기값은 매우 커지기 때문이다.

따라서 미분을 하기 전에 gaussian filter를 통과시켜서 noise를 제거한다.
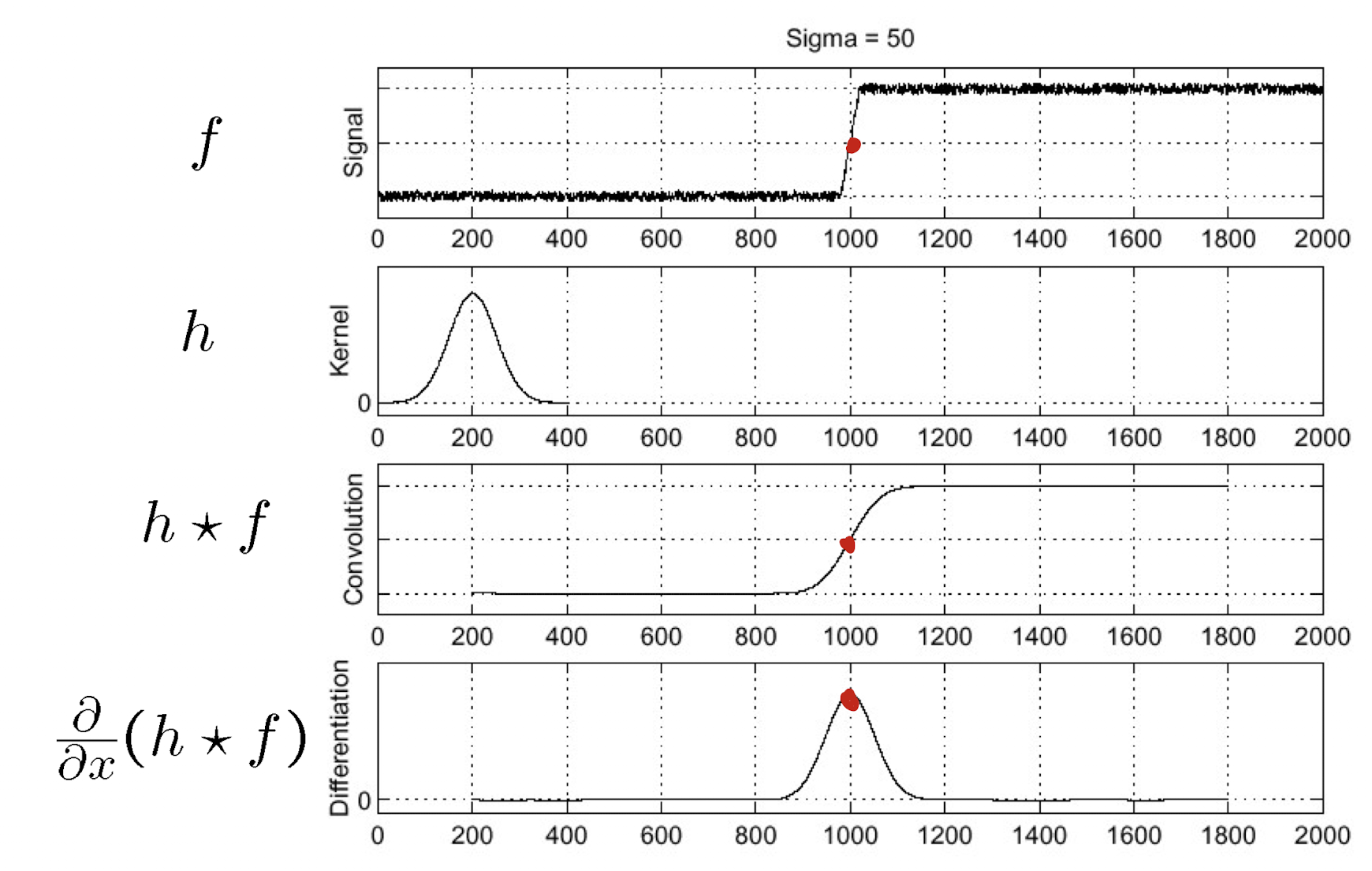
gaussian filtering으로 denoise를 해주고 미분을 하니 원하는대로 signal이 변하는 부분을 쉽게 캐치할 수 있는 것을 볼 수 있다.
이때 convolution 미분 연산을 아래와 같이 바꿀 수 있는 성질이 있는데 이를 이용하면 DoG(Derivative of Gaussian)을 만들어서 사용할 수 있다.
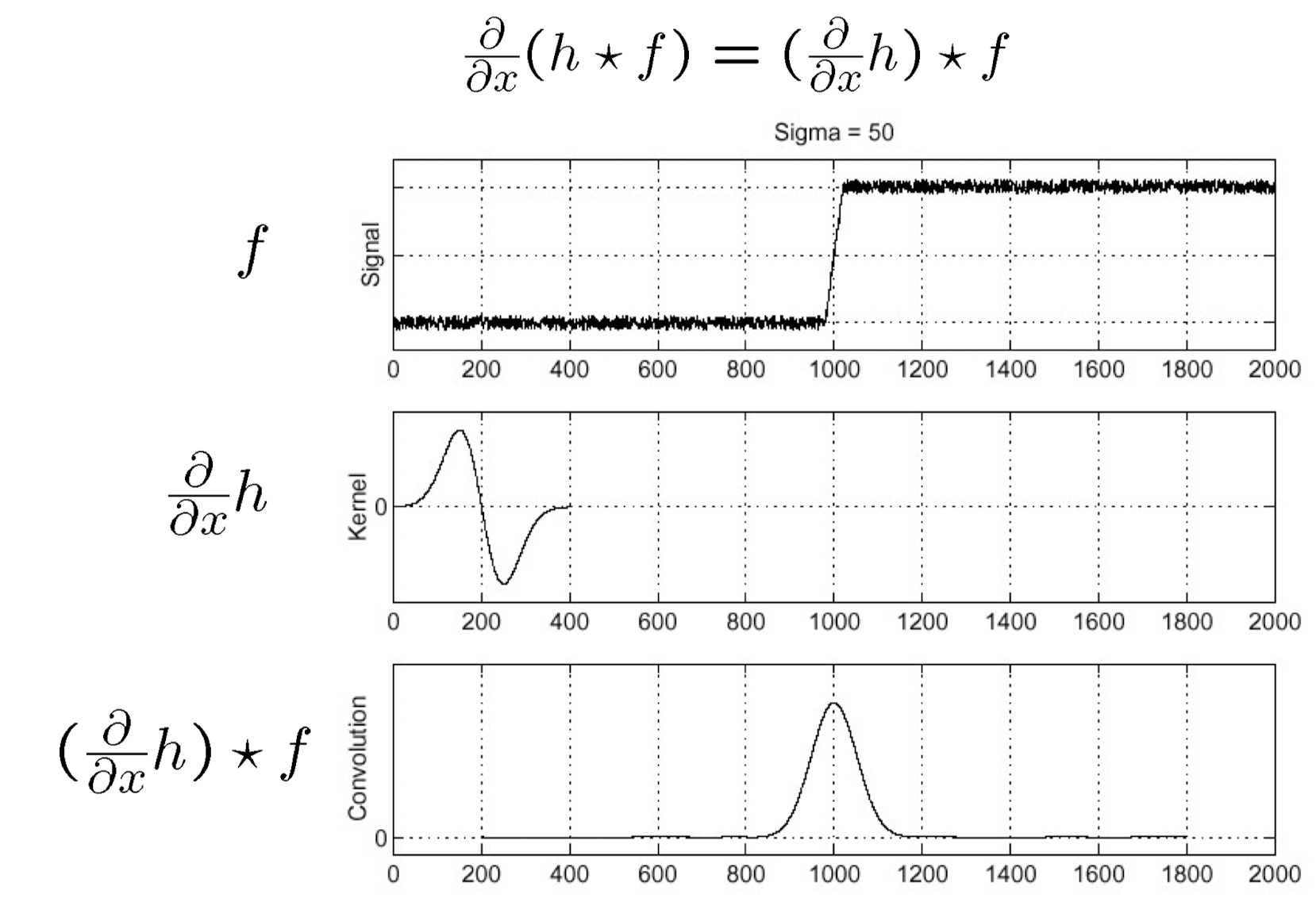
x방향이느냐 y방향이느냐에 따라 DoG는 아래와 같이 나타난다.
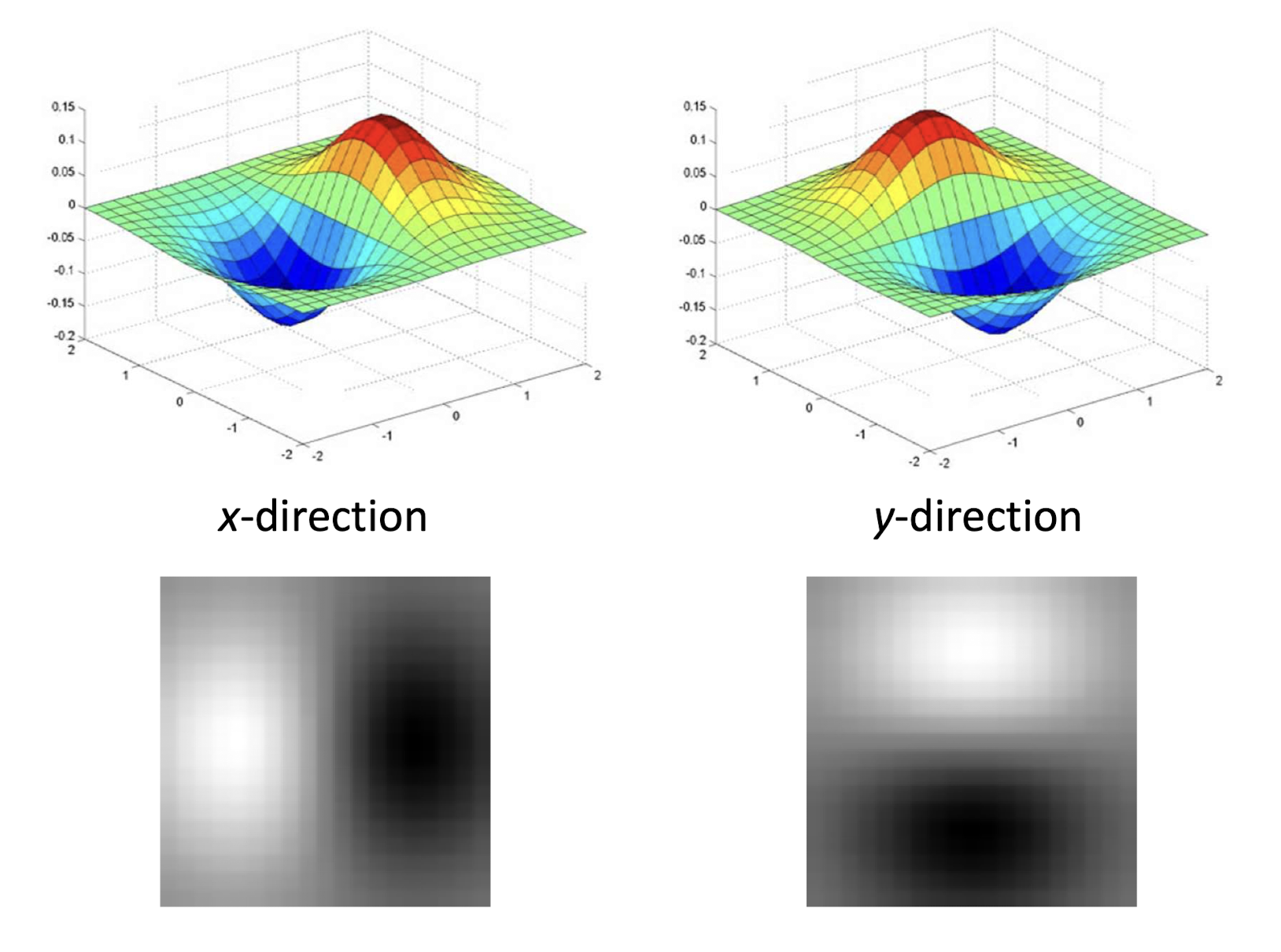
Sobel
Sobel 필터는 edge detection을 위한 필터로 DoG의 근사값으로 실제 구현한 필터이다.

필터의 크기가 커지면 localization 성능은 낮아지지만 noise에 덜 민감해져서 핵심 edge detection 성능이 오른다. 아래의 판다 사진 얘시를 통해 살펴보자.


필터가 커지니 대나무 부분들은 제거되고 핵심인 판다의 edge만 detection 되는 것을 볼 수 있다.
Thresholding
우선 x,y중 한방향만으로 필터를 돌릴 수는 없으니 gradient magnitude를 활용해서 아래와 같이 edge detection을 할 수 있다.

저런식으로 표시를 하려면 아래와 같이 Threshold를 임의로 정해야하는데 이런식으로 edge를 산정하면 edge의 두께가 너무 두꺼워져서 edge detection의 의미가 퇴색된다.
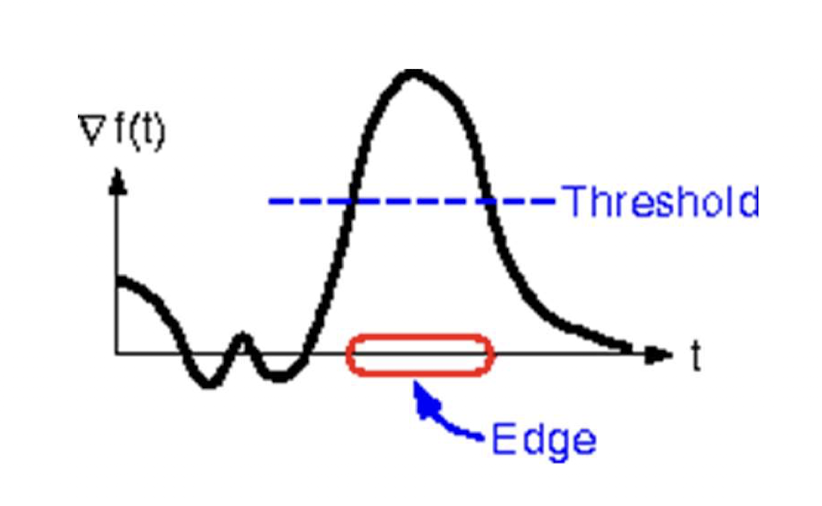
이를 개선하기 위해 thinning 말그대로 edge를 얇게만드는 과정이 필요하다. 이때 가장 많이 쓰이는 방식이 NMS(Non-Maximum Suppression)이다. 이는 Maximum이 아닌 값은 아예 0으로 보내버려서 maximum류(?)로 판단이 안되도록 해버리는 것이다. 진정한 local Maximum만 남기겠다는 것이다.

위의 Gradient Magnitude 표현에서 edge에 수직하는 방향을 gradient direction이라고 유추할 수 있다.

direction이 반드시 다음 픽셀을 통과하지 않을 수 있는데 그때는 linear interpolation을 통해 point를 만들어내서 계산한다.

Thinning을 진행하니 edge가 확실하게 잡힌 것을 볼 수 있다. 이때 edge를 좀더 잘 파악하고자 High threshold와 Low threshold를 이용하여 combined threshold를 이용하는 방법이 있다. 아래의 왼쪽 사진에서는 High threshold와 Low threshold를 각각 White와 Grey로 표시했고 combined threshold를 이용한 결과가 아래의 오른쪽 사진이다.

'Quality control (Univ. Study) > Digital Image Processing' 카테고리의 다른 글
| DIP 실습 - Median / Bilateral / Canny edge detection (0) | 2024.04.12 |
|---|---|
| Digital Image Processing - Subsampling (3) | 2024.04.10 |
| DIP 실습 - SpreadSalt Noise / Gradation / Editing (0) | 2024.04.03 |
| Digital Image Processing - Denoising / Filter / Edge Detection (1) | 2024.04.03 |
| Digital Image Processing - Filtering in Spatial Domain (0) | 2024.03.29 |



