Internal Processing of Digital Camera

위와 같이 H/W적인 과정과 S/W적인 과정이 모두 나타난 종합적인 Digital camera의 작동 과정이 요약되어 설명되어있다.

digital image는 위 그림과 같이 pixel(picture element)로 이루어져 있다.

좌측 그림을 sampling, quantization하면 우측그림처럼된다.
Image resolution
이미지 해상도는 디지털 이미지의 세밀함과 정확도를 결정하는 중요한 요소다. 해상도는 크게 두 가지로 나뉜다: 공간 해상도와 강도 해상도다.
공간 해상도는 이미지를 구성하는 픽셀의 밀도로, 특정 단위 면적 당 픽셀의 수를 의미한다. 일반적으로 dpi(dots per inch)라는 단위로 표현되며, 인쇄물에서 매우 중요하다. dpi가 높을수록 한 인치당 더 많은 점이 있음을 의미하고, 이는 이미지가 더 선명하고 상세하게 출력됨을 뜻한다.
강도 해상도는 이미지의 명암 차이를 얼마나 잘 구분할 수 있는지를 나타내는 것으로, 이미지의 각 픽셀이 표현할 수 있는 색상의 미묘한 차이를 말한다. 이는 비트로 측정되며, 비트 수가 많을수록 이미지에서 더 다양한 색상과 명암을 나타낼 수 있다.
해상도의 기본 원칙은 간단하다. 고정된 범위 안에서 픽셀 수가 많을수록, 즉 더 많은 샘플이 있을수록 해상도가 높아진다. 또한, 픽셀 하나가 나타낼 수 있는 색상의 수, 즉 비트 수가 많아질수록 해상도는 높아진다. 이는 이미지가 더욱 세밀하고 정교하게 표현될 수 있음을 의미한다.
높은 해상도의 이미지는 더 많은 정보를 담고 있어, 이미지 편집 시 더 정밀한 조작이 가능하고, 품질이 좋은 출력물을 얻을 수 있다. 반면 낮은 해상도의 이미지는 픽셀화 현상이 눈에 띄고, 세부 사항이 뭉개지거나 불명확해질 수 있다. 따라서 사진 촬영, 이미지 편집, 인쇄 등에서 원하는 결과물을 얻기 위해서는 적절한 해상도 설정이 필수적이다.
Uniform Sampling
Nyquist 이론은 신호 처리에서 매우 중요한 개념이다. 이 이론에 따르면, 연속적인 신호를 디지털로 변환하기 위해서는 원본 신호의 최대 주파수의 두 배 이상으로 샘플링해야 한다. 즉, 샘플링 주파수가 원본 신호의 최대 주파수의 두 배 이상이어야 원본 신호를 완벽하게 복구할 수 있다는 것이다.
Aliasing은 샘플링 과정에서 발생할 수 있는 문제다. 샘플링 주파수가 Nyquist 이론에 의해 정의된 최소한의 주파수보다 낮을 때 발생한다. 이 경우, 높은 주파수의 신호가 낮은 주파수의 신호로 잘못 해석되어 신호가 왜곡될 수 있다. 이를 aliasing 현상이라고 부르며, 이를 방지하기 위해 적절한 샘플링 주파수 선택과 함께 저주파 통과 필터(Low-pass filter)를 사용하기도 한다.
간단히 말해서, Nyquist 이론은 디지털 신호 처리에서 신호를 제대로 샘플링하고 복구하기 위한 기준을 제공한다. 반면, aliasing은 이 기준을 충족시키지 않을 때 발생하는 문제로, 신호의 왜곡을 초래할 수 있다. 따라서, 고품질의 디지털 신호 처리를 위해서는 Nyquist 이론을 잘 이해하고 적용해야 하며, aliasing을 피하기 위한 적절한 조치를 취해야 한다.
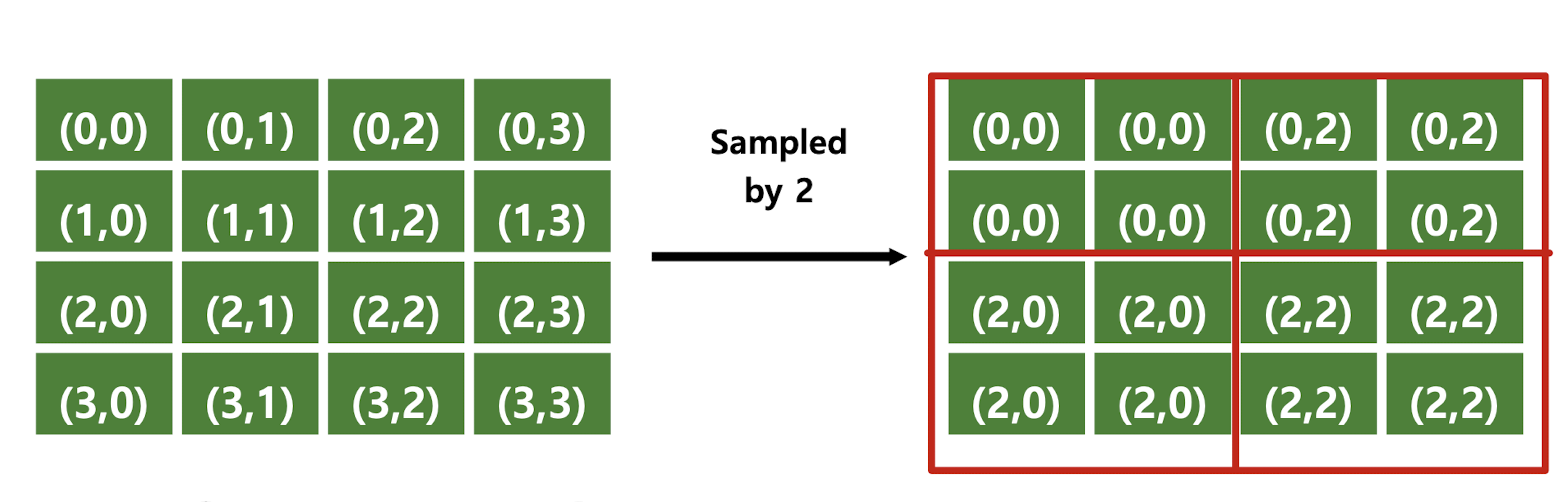
이미지에서는 sampled by 2라면 2X2에서 sampling하여 하나로 통일 하겠다는 뜻이다. 이제 sampling 크기에 따라 화질의 변화를 확인해보자. 아래 그림은 undersampling을 다양한 값으로 해본 것이다.

이때 주파수가 높은 부분, 위 그림에서는 체크무늬 책상이나 바지같은 부분에서 물결무늬가 나타나는 것을 모아레 패턴이라고 한다. 고주파 신호일 수록 sampling 범위가 조금만 넓어져도 그 특성을 반영할 수가 없는 상태가 되어 발생하는 문제이다.

위 그림은 uniform quantization이다. gray scale에서 원래 0~255 8 bits로 표현되던 사진을 비트수를 낮춰가며 살펴본 결과이다.

위 그림은 Digital Camera에서 Color Sensing을 하는 방식이다. Bayer grid 형태에서 각 센서들은 RGB중 해당하는 색만 인식할 수 있는 특정 빛 세기만 측정하는 센서가 달려있다. Demosaicing을 위해 각 픽셀의 주변부 빛들의 값을 통해 interpolation을 하여 자연스러운 실제 색과 가깝게 구현한다.
'Univ. Study > Digital Image Processing' 카테고리의 다른 글
| Digital Image Processing - Denoising / Filter / Edge Detection (1) | 2024.04.03 |
|---|---|
| Digital Image Processing - Filtering in Spatial Domain (0) | 2024.03.29 |
| Digital Image Processing - Pixel Processing / 히스토그램 (1) | 2024.03.26 |
| Digital Image Processing - 기본 지식(1) (0) | 2024.03.17 |
| Digital Image Processing - Intro (1) | 2024.03.13 |



