Convolution
선현대수학 수업을 정리할 때도 기록했었고 CNN부터 시작해서 이미지를 처리하는 다양한 딥러닝 논문들을 공부할때 Convolution layer가 없는 논문을 찾기가 힘들 정도기 때문에 많이 다뤄봤으니 간단하게만 살펴보자.
우선 아래는 1D Convolution이다. 한 함수를 뒤집어서 이동시키며 겹치는 부분의 넓이를 구하는 개념이고 적분식은 바로 아래처럼 표현된다.
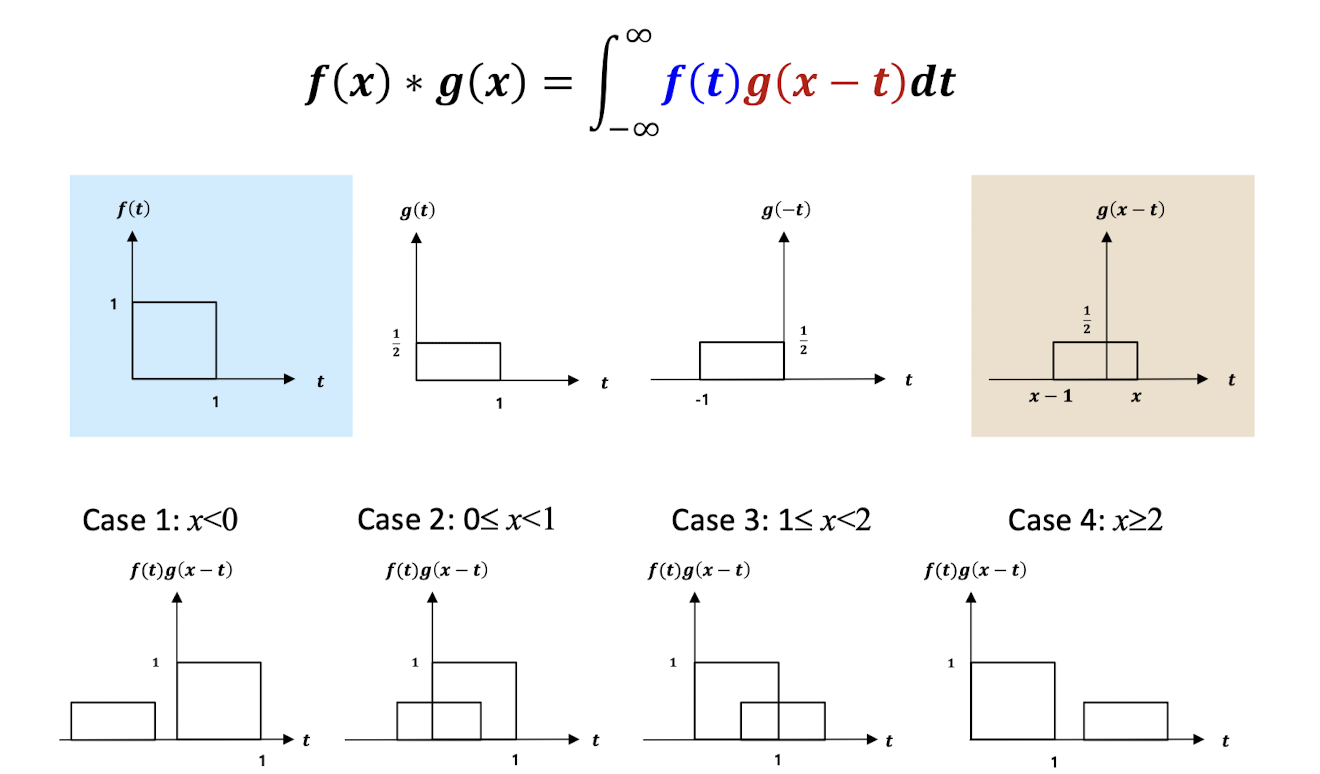
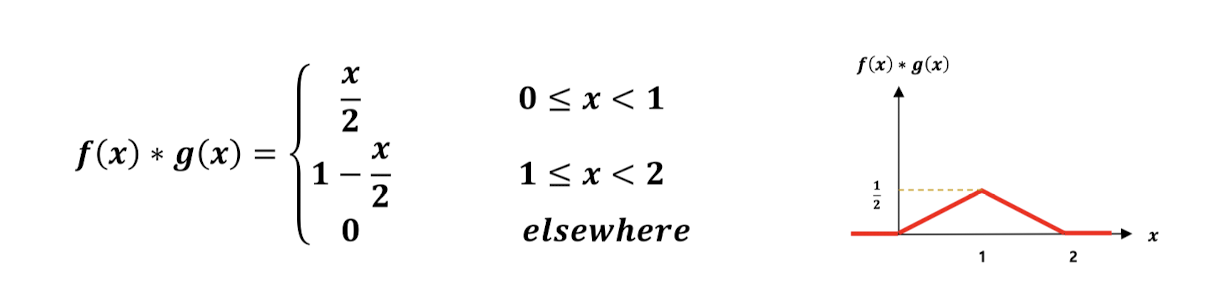
이를 확장한 2D Convolution이 본격적으로 이미지 처리를 위해 쓰이는 filter에서 사용되는 연산이다.
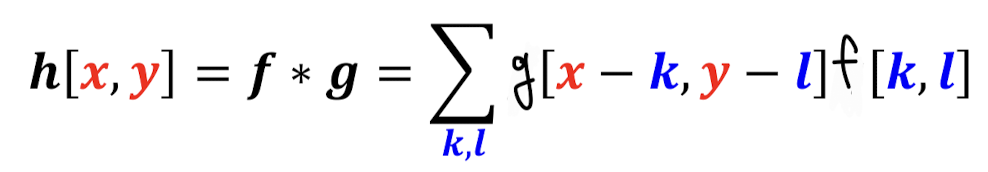
아까 봤던 개념처럼 filter인 g를 뒤집어서 겹쳐서 연산을 하는 과정이다. 참고로 f는 source image라고 보면 된다.

이런 뒤집는 관점이 마음에 안들면 아래와 같이 Correlation Filtering을 이용하면 된다.
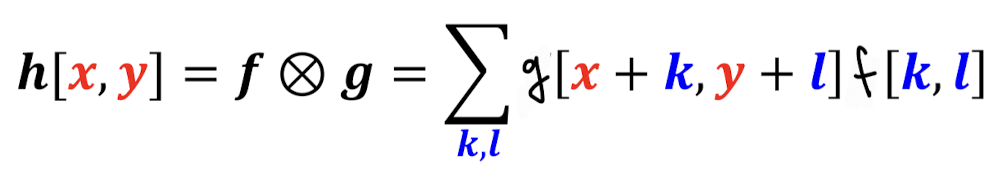

Filtering
필터링은 local neighbor를 이용하여 중앙 위치의 pixel 값을 바꾸는 것이다. 따라서 주변과의 연관성이 값에 포함된다. 필터링은 흔히 아래와 같은 경우에 쓰인다.
Enhance images
Denoise, resize, increase contrast, etc.
Extract information from images
Texture, edges, distinctive points, etc.
Detect patterns
Template matching
예를 통해 살펴보자.
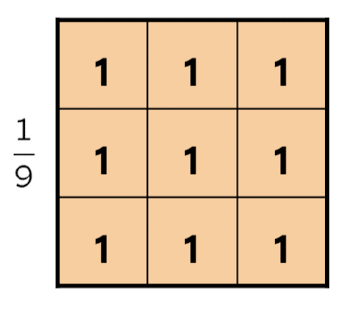
위와 같은 filter를 이용하면 주변의 값들과 본인의 값을 평균을 내는 방식이 적용되기 때문에 smoothing filter의 역할을 하게된다.

Matrix에서 2D Convolution 계산 과정을 살펴보자.


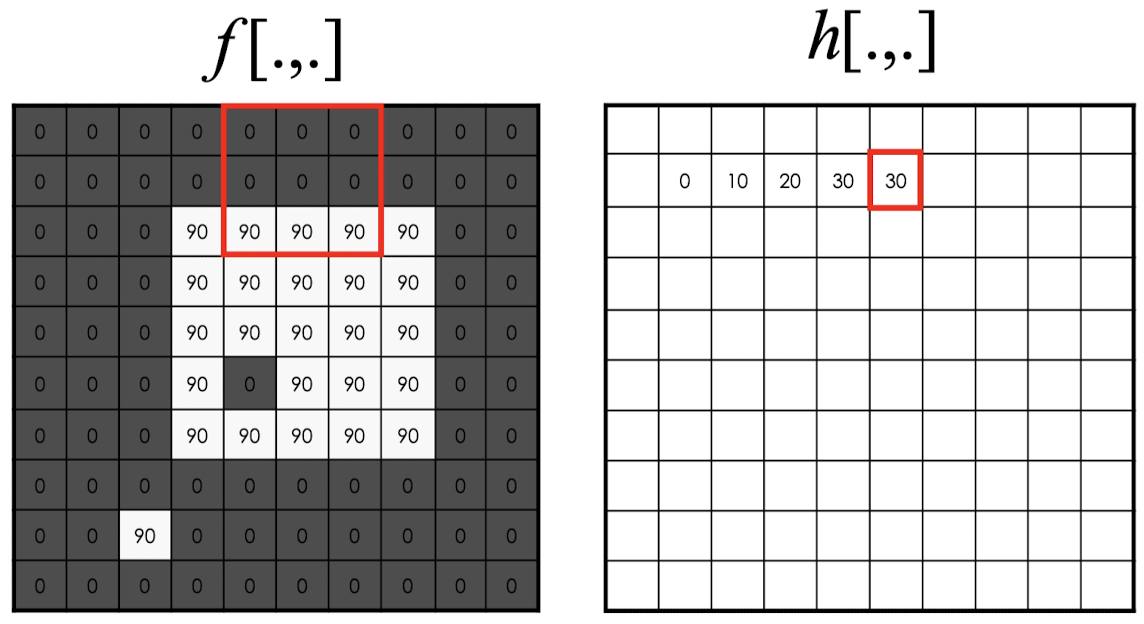
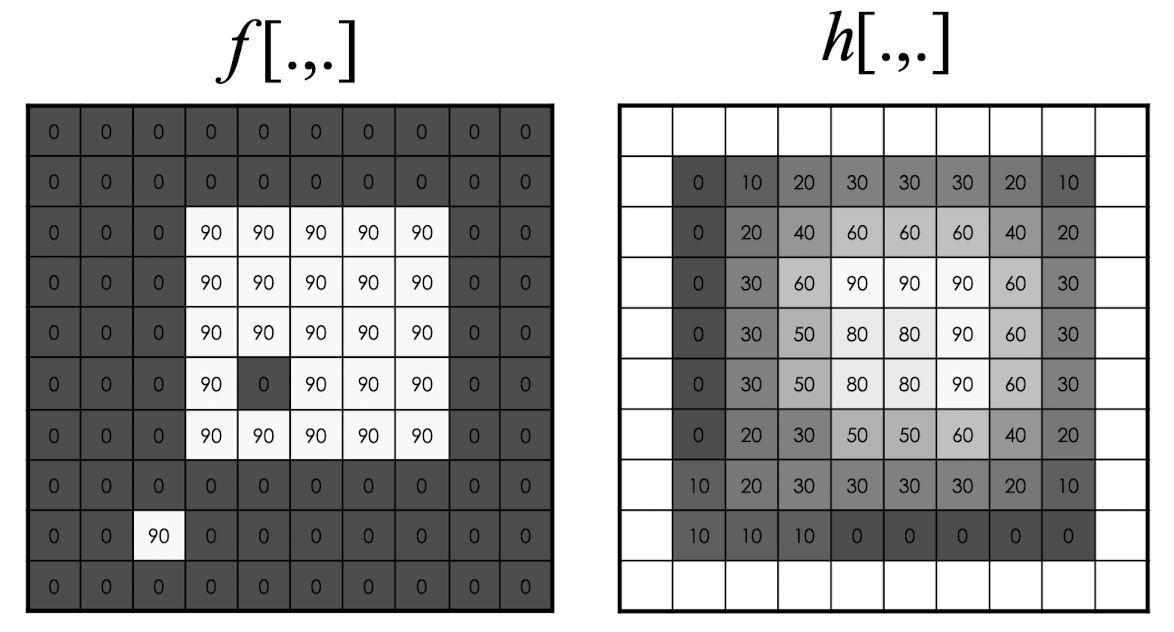
연산을 모두 돌리면 위와 같은 결과가 나온다.
Gaussian Filter
가우시안 필터는 가까울수록 가중치가 높아져서 자연에서 볼 수 있는 정규분포를 반영한 필터이다.
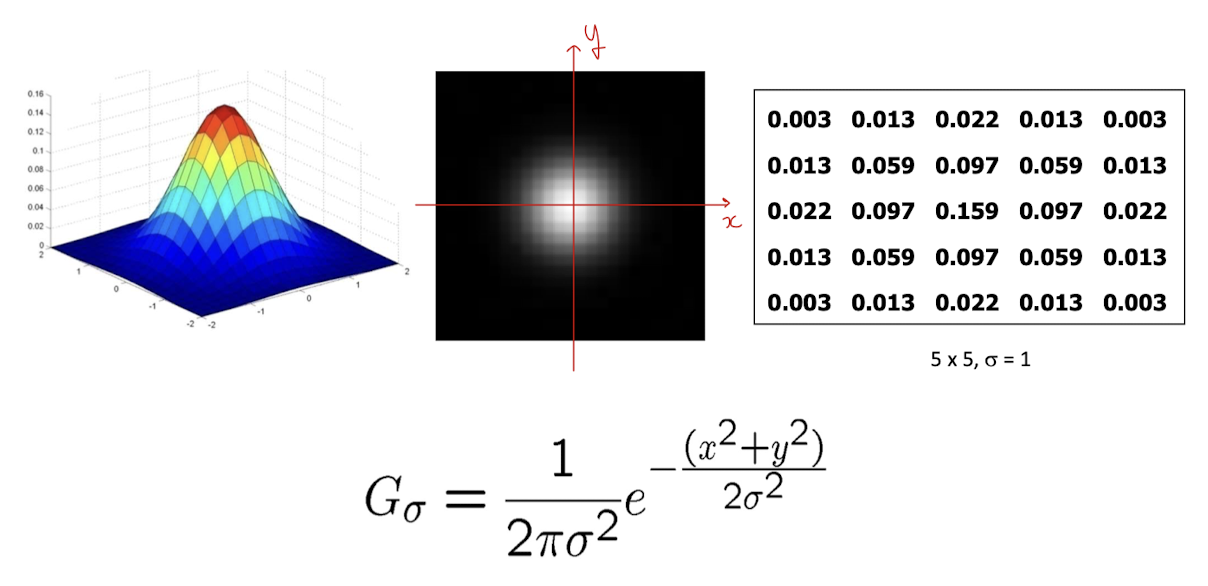
가우시안 필터를 이용하여 위에서 봤던 사진을 필터링하면 아래와 같은 결과가 나온다.

가우시안필터는 고주파를 필터링하는 low-pass filter이다.
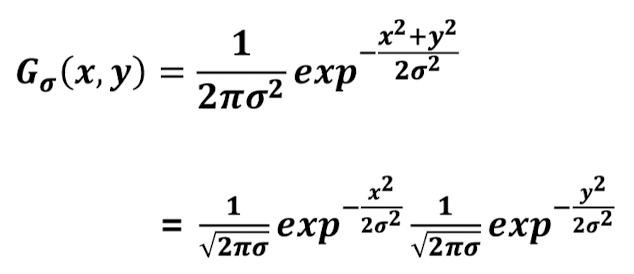
위는 gaussian filter의 separability를 보여주는 식이다.
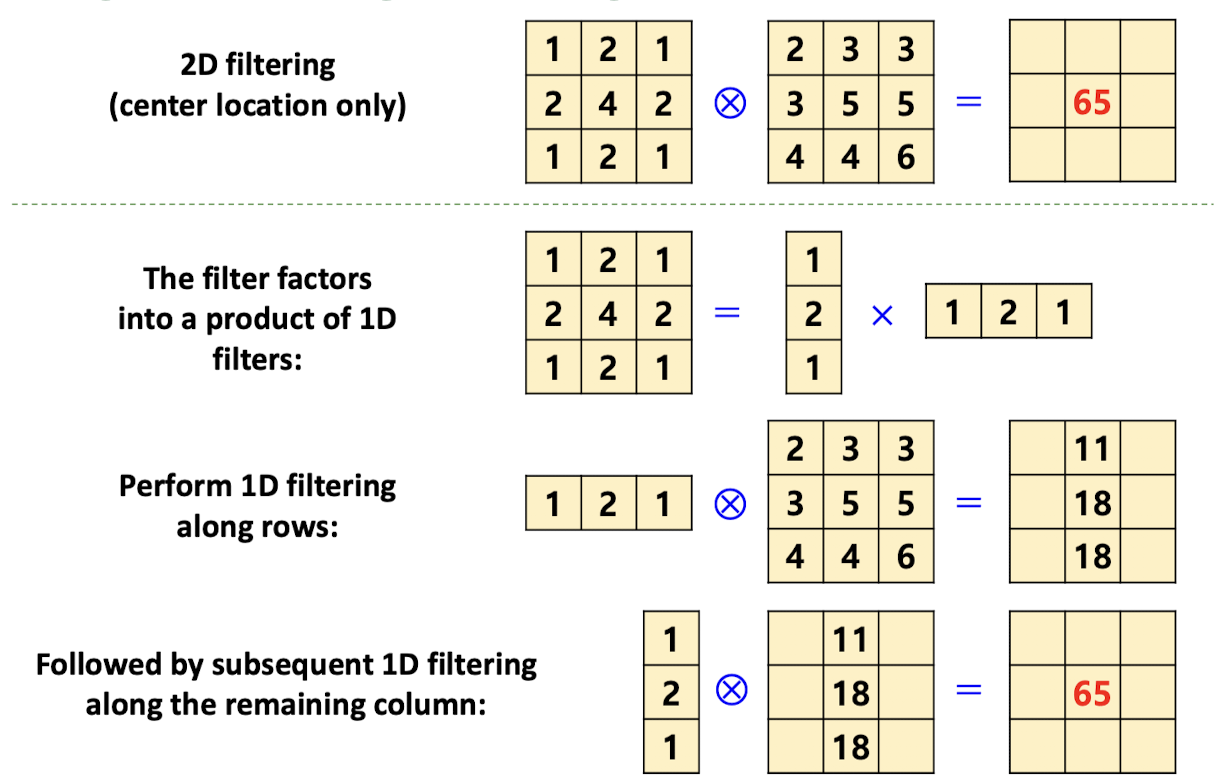
Separability 특징을 이용하여 위와 같이 convolution 연산을 순차적으로 진행하면 matrix의 크기가 커졌을때 메모리와 연산량을 줄여서 H/W 친화적으로 경량화가 가능하다.
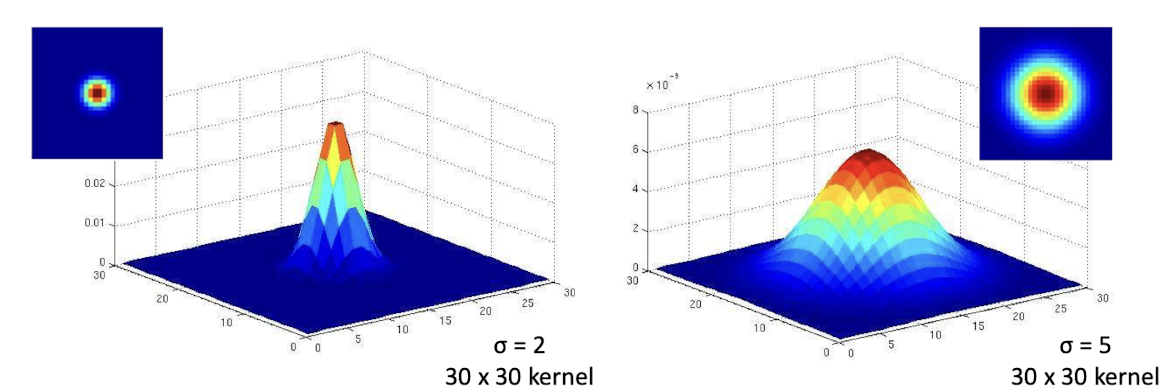
가우시안 필터를 사용할때는 위와 같이 무한히 커질 수 있기 때문에 연산량 조절을 위해 3σ 범위를 이용했을 때 99%를 커버할 수 있다는 통계학적인 지식을 이용하여 적절한 사이즈의 filter를 만드는 것도 중요하다.
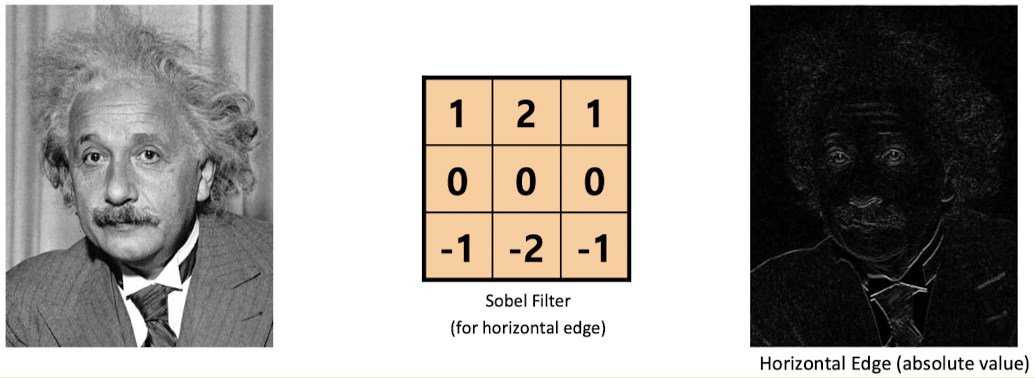
이외에도 좌우변화에 반응하는 필터와
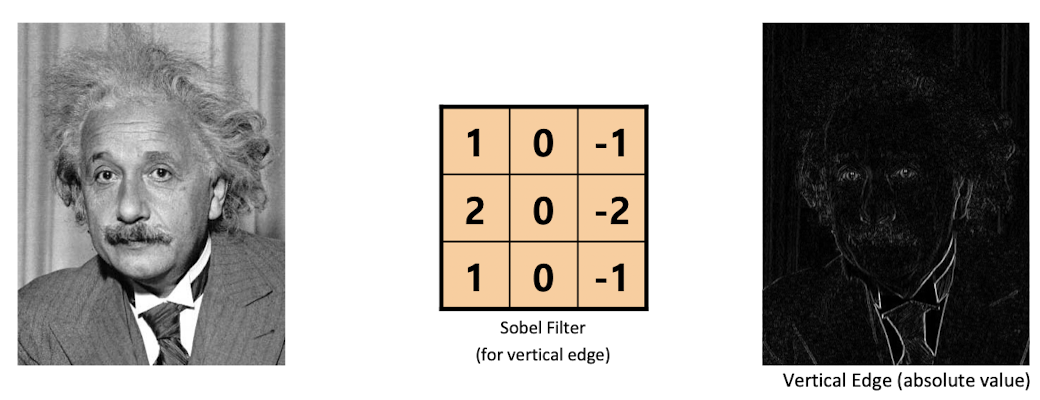
상하변화에 반응하는 필터는 이렇게 작동한다.
Bilateral Filter
단순히 가우스 필터를 이용하면 아래와 같이 blur처리가 되어버린다.

Bilateral Filter를 이용하면 이미지의 특징은 좀더 살려서 smoothing을 할 수 있다.
필터의 모양을 보면 이미지의 모양을 반영하는 것을 알 수 있다.

이는 Bilateral Filter가 아래와 같은 수식을 따르기 때문이다.

not new부분은 기존의 가우시안처럼 위치에 따라 가까울수록 가중치를 높이고 new 부분은 밝기 차이가 많이나면 가중치가 줄어들어 반영되지 않도록 한다.
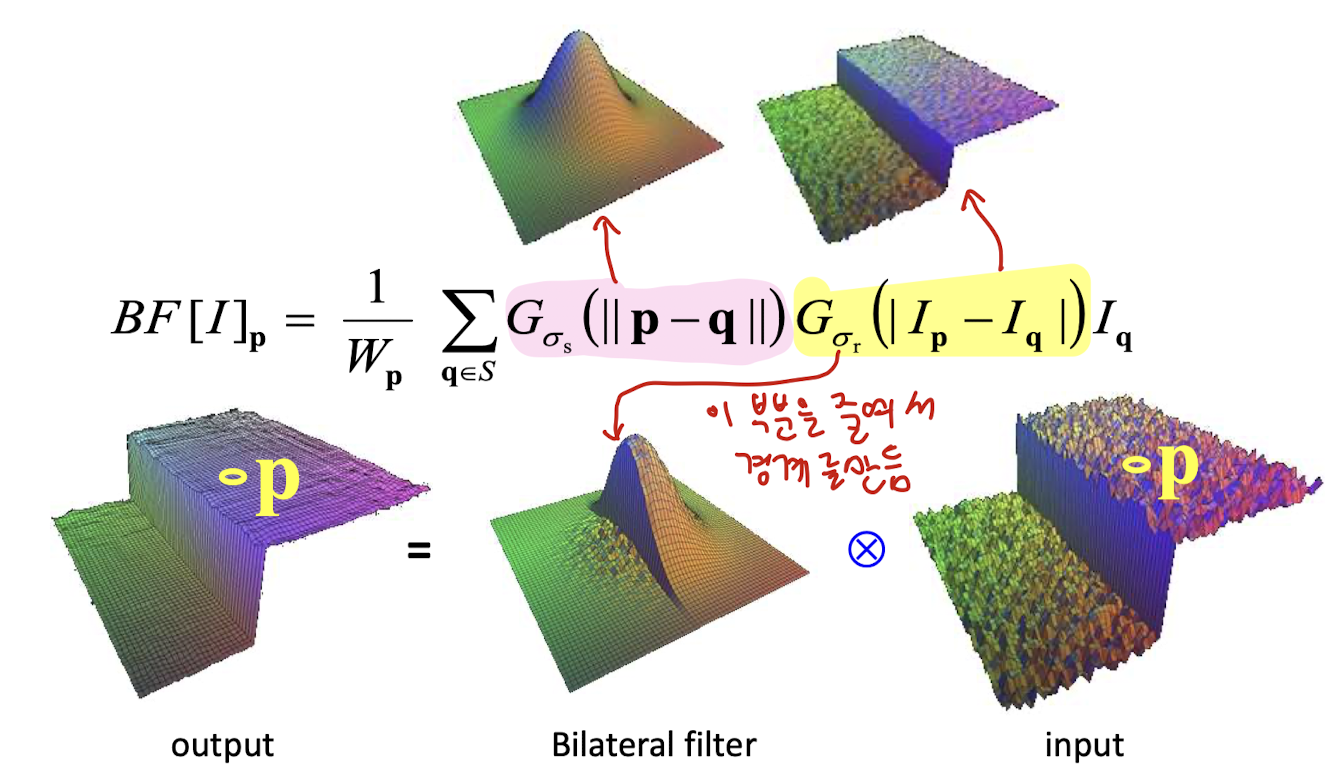
실제 예시를 살펴보면 위와 같다. 변수 설정에 따라 아래와 같이 변화하는 것도 볼 수 있다.

'Univ. Study > Digital Image Processing' 카테고리의 다른 글
| DIP 실습 - SpreadSalt Noise / Gradation / Editing (0) | 2024.04.03 |
|---|---|
| Digital Image Processing - Denoising / Filter / Edge Detection (1) | 2024.04.03 |
| Digital Image Processing - Pixel Processing / 히스토그램 (1) | 2024.03.26 |
| Digital Image Processing - 기본지식(2) (0) | 2024.03.22 |
| Digital Image Processing - 기본 지식(1) (0) | 2024.03.17 |



