Function of Two Random Variables
Two random variables의 기댓값을 구하는 식은 아래와 같다.
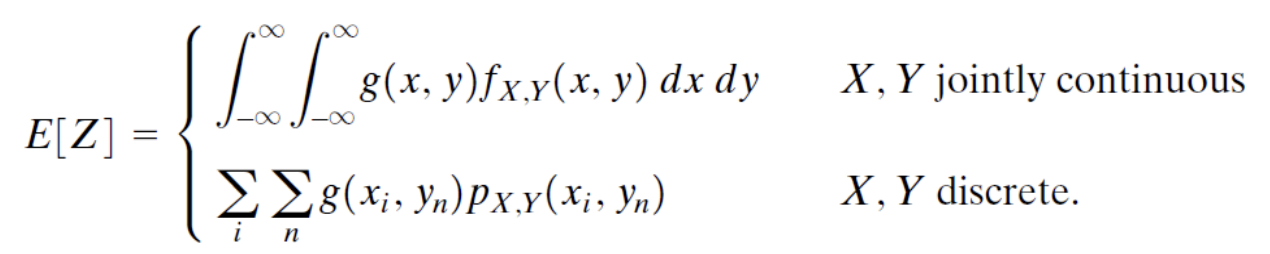
이를 이용한 Z = X + Y인 예시를 풀어보면 아래와 같이된다.
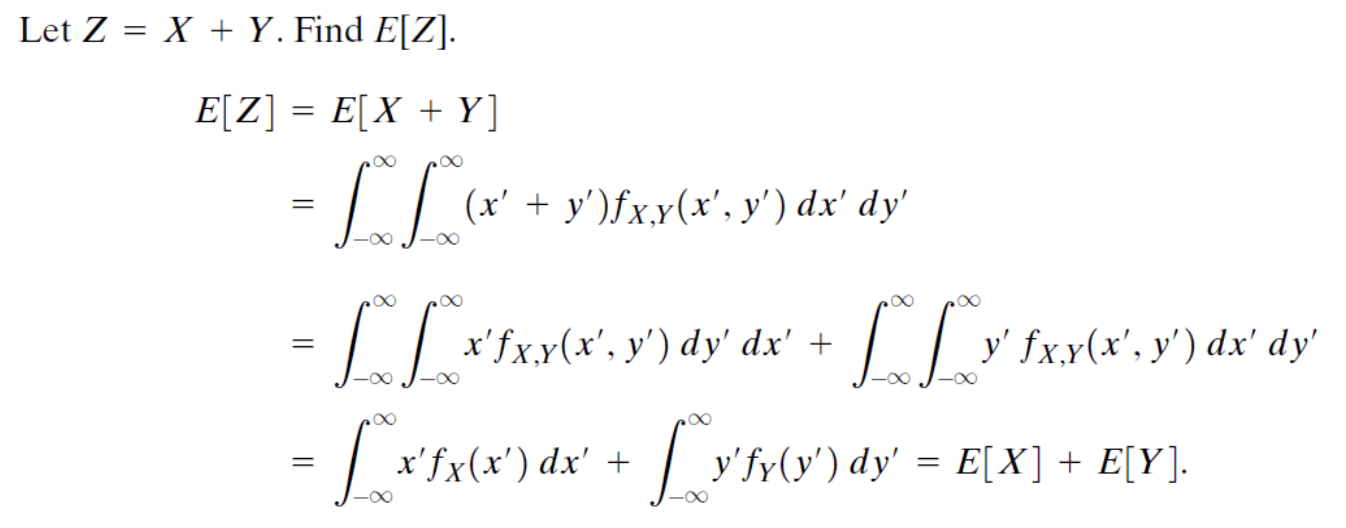
다음은 독립인 경우의 예시이다.
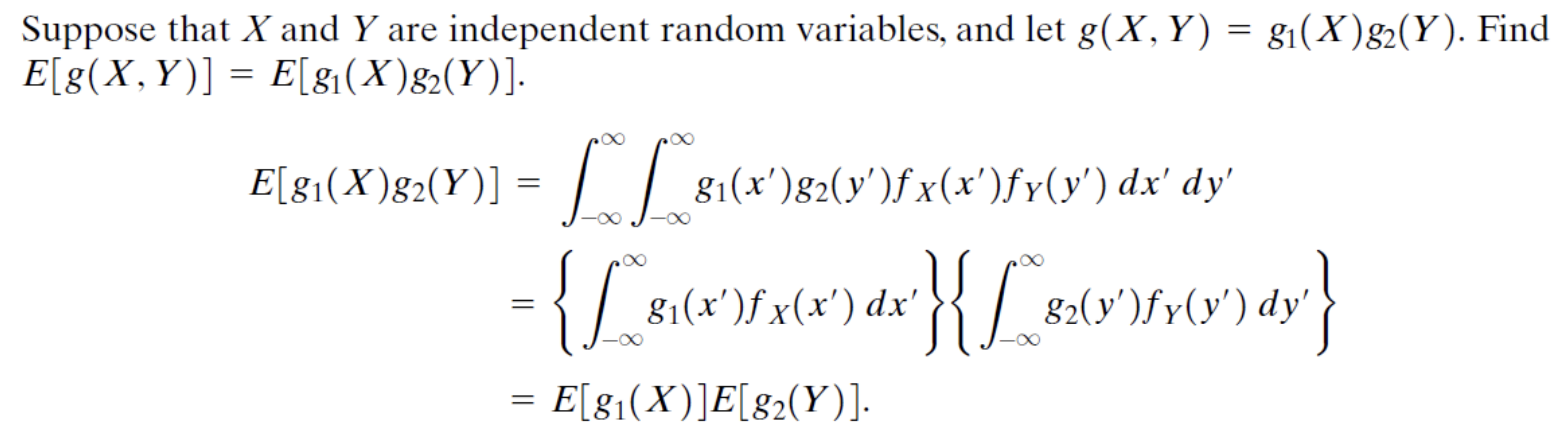
Joint Moments, Correlation, and Covariance
X와 Y의 jk번째 joint moment는 아래와 같다.
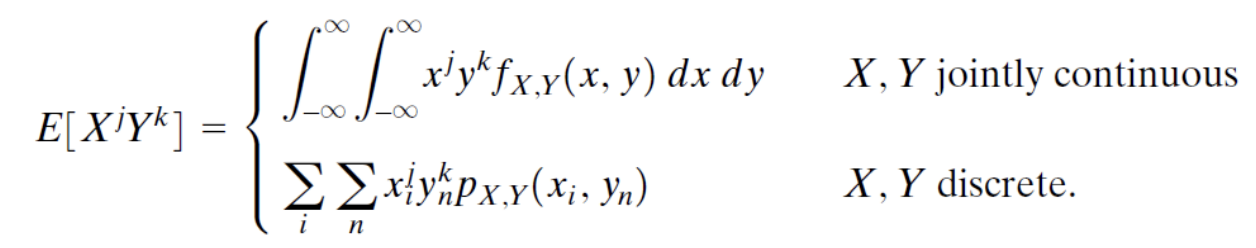
X와 Y의 Correlation의 정의는 E[XY]이다.
이때 E[XY]=0이면 X와 Y는 orthogonal하다고 한다. 또한 E[XY]=E[x]E[Y]이면 X와 Y가 uncorrelated하다고 한다.
이는 결국X와 Y가 독립이면 uncorrelated하다는 뜻이다. 그 역은 성립하지 않지만 X와 Y가 jointly Gaussian이면 성립한다.
X와 Y의 jk번째 central moment는 아래와 같다.

X와 Y의 Covariance는 아래와 같이 정의된다.

위의 식에서 쉽게 추론할 수 있듯이 만약 X와 Y가 independent하다면 Covariance는 0이 된다.
따라서 COV(X,Y)=0이면 X와 Y는 uncorrelated라는 결론을 도출할 수 있다.
추가적으로 X와 Y가 orthogonal하면 COV(X,Y)=-E[X]E[Y]이라는 것을 알 수 있다.

Conditional Probability
Conditional CDF를 먼저 살펴보면 아래와 같다.
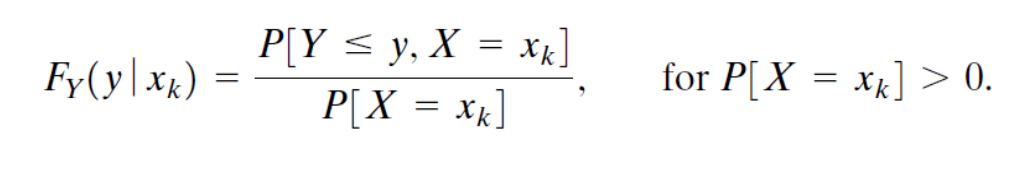
Conditional CDF를 미분하여 구한 Conditional PDF이다.
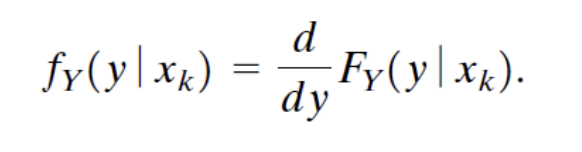
이때 X가 Discrete RV인 경우 아래와 같다.

다음은 X가 Continuous RV인 경우이다.


Conditional Expectaion
X=x라고 주어져 있을때 Y의 Conditional Expectaion은 다음과 같이 정의된다.

X와 Y가 모두 discrete한 특수한 경우에는 아래와 같다.
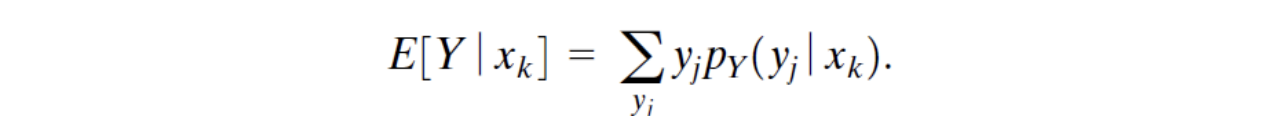
E[Y|x]를 X에 대한 함수로 보면 g(X)=E[Y|X]로 둘 수 있고 E[g(X)]=E[E[Y|X]]라고 할 수 있다.
이때 X가 continuos인 경우와 discrete한 경우를 나눠서 살펴보면 아래와 같이 식을 쓸 수 있다.
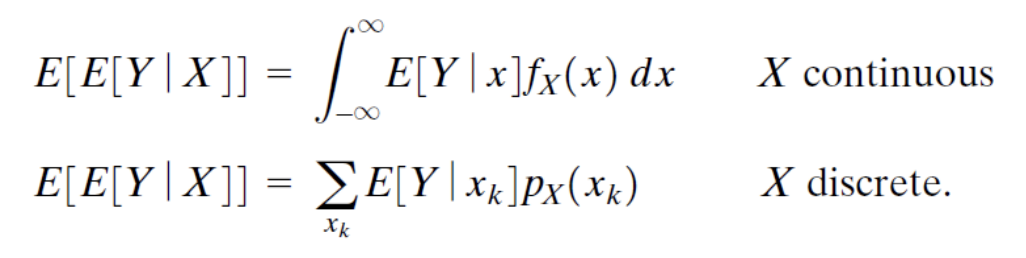
그리고 연속인 경우에는 아래와 같이 식을 계산하여 결과를 얻을 수 있다.
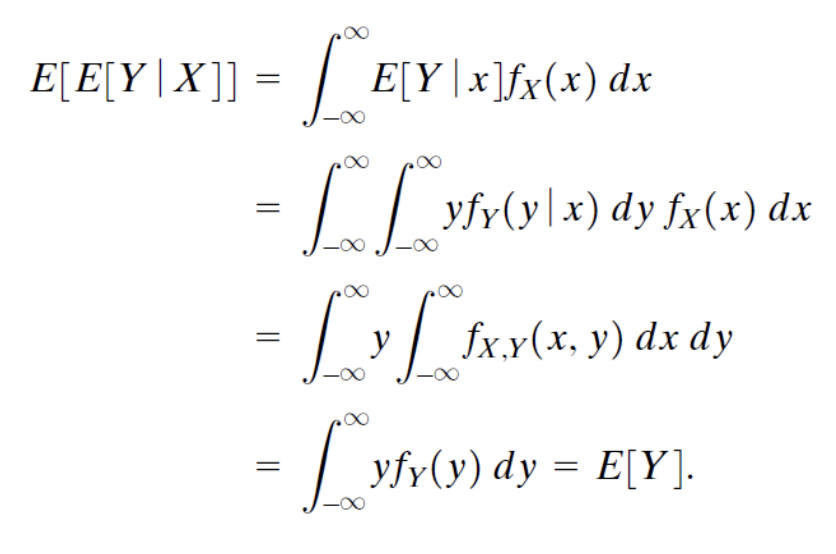
따라서 일반적으로 다음의 식이 성립한다.

Functions of Two Random Variables

이전에는 위와 같은 조건의 문제를 푸는 과정이었다면 이제는 아래와 같이 두개의 RV로 표현된 Z에 대해서 구하는 방법을 알아보자.

이때 Z의 CDF는 항상 그렇듯이 아래와 같이 표현할 수 있다.
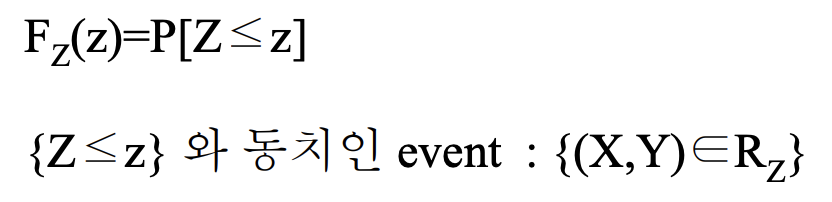
이때 Z<=z 범위에 해당하는 X,Y의 범위를 찾아서 아래의 적분식을 풀어내는 것이 핵심이다.
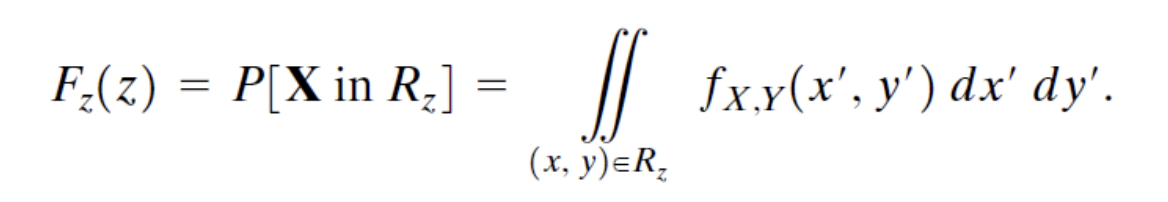
이 방식으로 위에서 봤던 예시를 다시 한번 살펴보자.
"Z=X+Y의 CDF와 PDF를 구해라!"
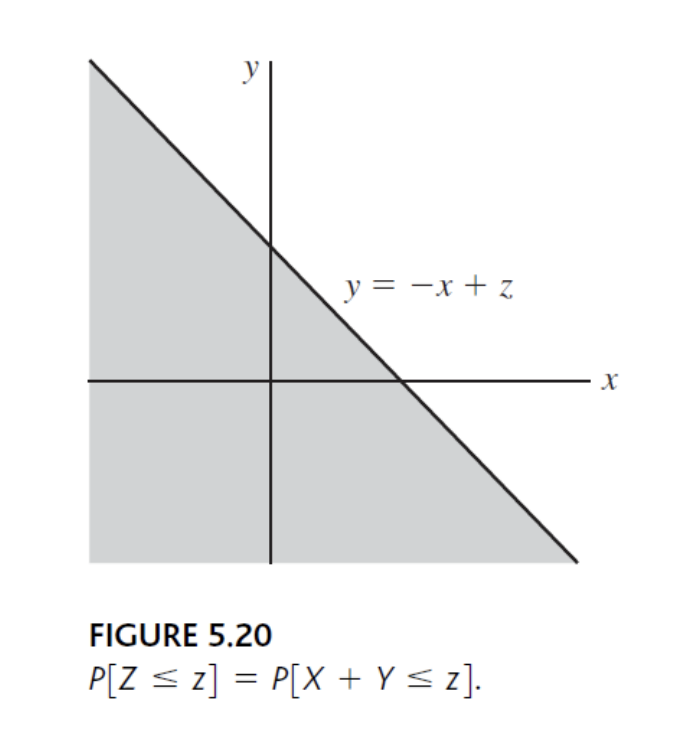
CDF의 그래프는 위와 같이 그릴 수 있고 그 식은 아래와 같이 작성할 수 있다.

이때 CDF를 미분함으로써 PDF도 구할 수 있다.
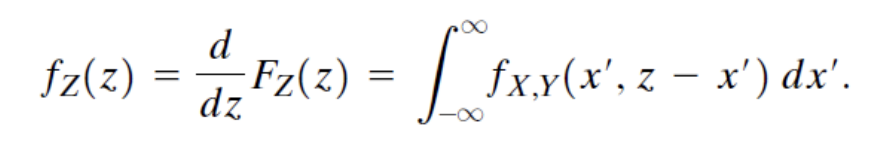
이때 X와 Y가 독립이라면 아래와 같이 convolution integral 형식으로 표현될 수 있다.
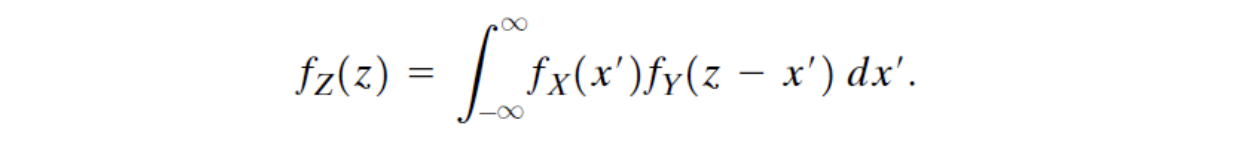
X와 Y가 Nonindependent Gaussian RV라면 아래와 같이 표현될 수 있다는 것을 쉽게 유추할 수 있다.
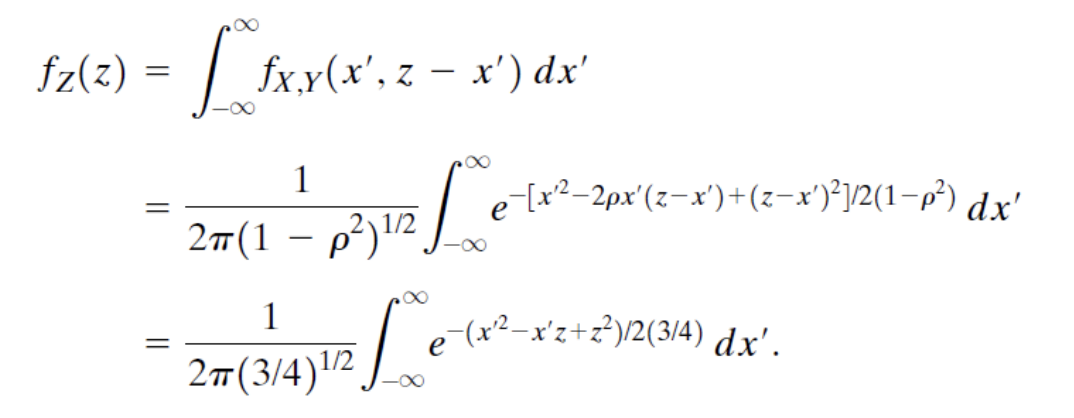
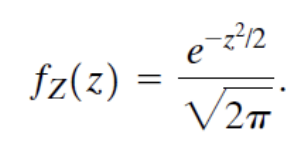
위는 평균이 0이고 unit-variance인 경우이다.
이번에는 조금 다른 예시도 살펴보자.
"Z=X/Y의 CDF와 PDF를 구해라!"
위의 문제를 풀려면 아래와 같이 두 단계를 거쳐서 풀 수 있다.

Transformations of Two Random Variables
이제는 조금더 나아가서 새로운 조건의 문제 상황을 해결해보자.

위 문제는 영역을 두개를 찾고 그 교집합 범위에 대해서 적분하는 방식을 통해 풀 수 있다.
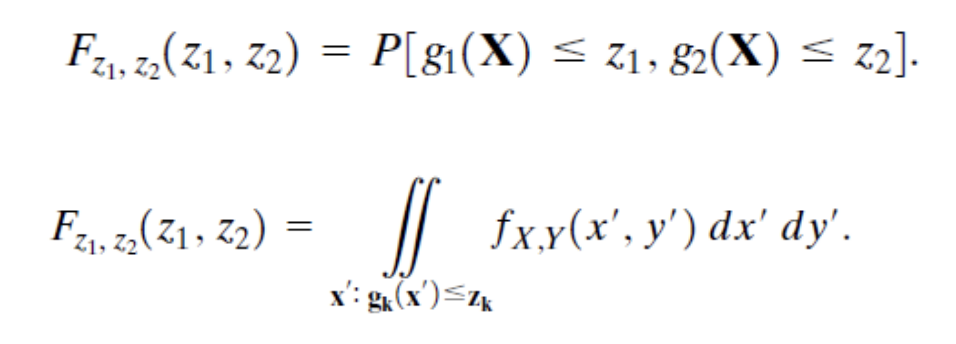
W=min(X,Y)이고 Z=max(X,Y)인 상황에서 CDF를 구해보자.


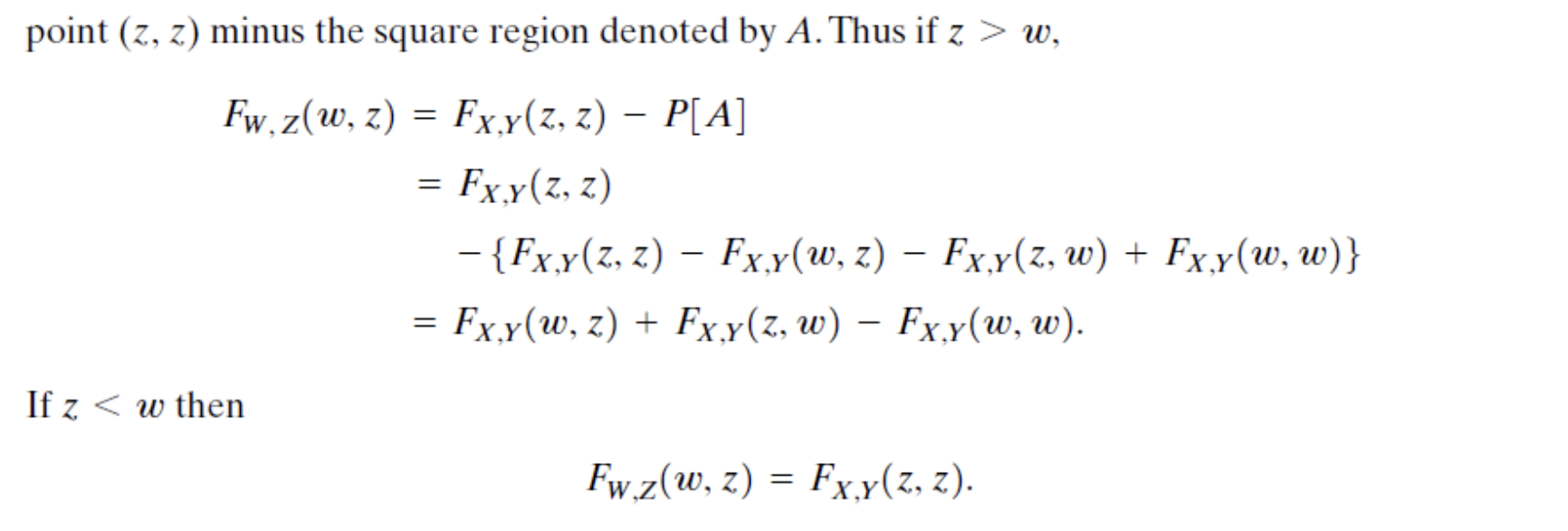
PDF of Linear Transformations
위의 문제상황은 선형 변환을 통해서도 풀이될 수 있다.

이때의 풀이방법은 두가지가 있다.
1)
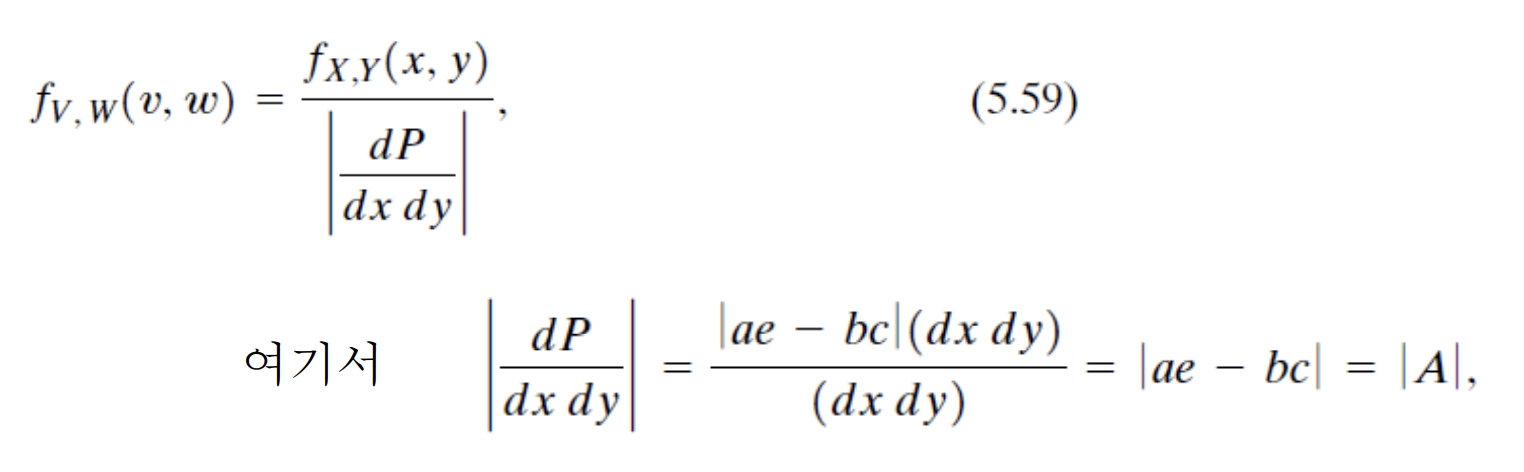
2)

2번 풀이법이 조금 더 간단하여 det(A)값을 이용하는 방식을 이용하도록 한다.
이를 이용하여 Jointly Gaussian Random Variables X,Y에 대한 예시를 풀어보면 아래와 같다.
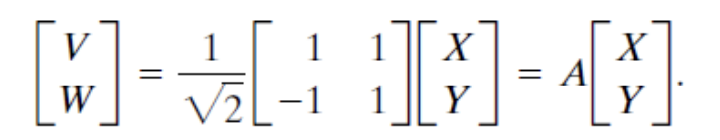
A를 역변환하면
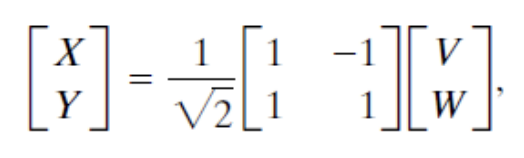
따라서 아래와 같이 표현할 수 있다.

따라서 V와 W에 대한 PDF를 구하면 아래와 같다.
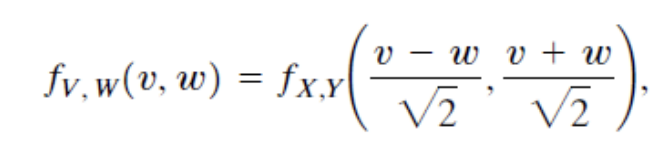

구한 PDF를 x,y가 아닌 v,w로 표현을 하면 아래와 같다.


Pairs of Jointly Gaussian Random Variables

Gaussian RV의 경우 몇가지 특징이 있다.


위의 식에서 ρX,Y 가 X와 Y의 correlation coefficient 임을 보이면 아래와 같다.

Rotation of Jointly Gaussian Random Variables
임의의 2차원 가우스 벡터에 해당하는 타원이 각도를 형성한다.
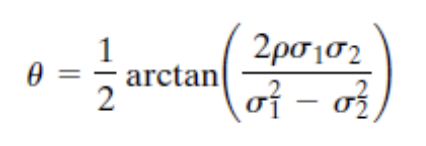
다음의 rotation matrix를 이용하여 COV(V,W)=0임을 알아보자.

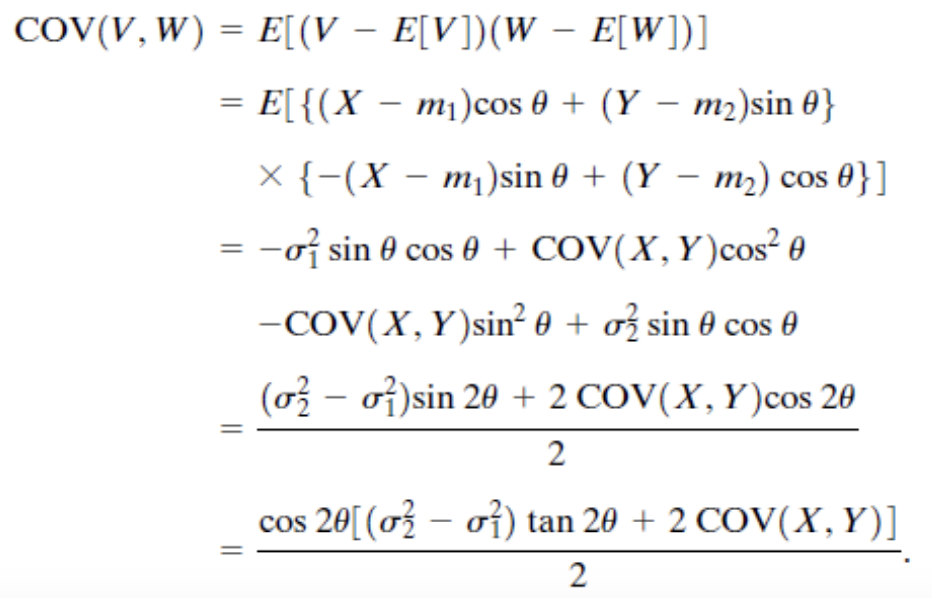
위 식에 우리가 설정한 아래의 angle of rotaion θ를 대입하면 COV(X,Y)=0임을 알 수 있다.

'Quality control (Univ. Study) > Probability and Random Variables' 카테고리의 다른 글
| Lecture 8 - Vector Random Variables (0) | 2023.05.27 |
|---|---|
| Lecture 6 - Pairs of Random Variables(1) (0) | 2023.05.25 |
| Lecture 5 - Continuous Random Variables (0) | 2023.05.20 |
| Lecture 4 - One Random Variable (0) | 2023.05.13 |
| Lecture3 - Discrete Random Variable (0) | 2023.04.14 |



