Cumulative Distribution Function (CDF)
CDF의 정의는 다음과 같다.


X <= x에 해당하는 outcome들에 대한 확률의 합 x의 함수이다.
다음은 CDF를 이해하기 위한 간단한 예시이다.

위의 경우에 대한 CDF를 그려보면 다음과 같다.

y값은 차례로 1/8, 1/2, 7/8, 1이 될 것이다. 이는 1/8, 3/8, 3/8, 1/8을 차례로 더해가는 값이다.
이를 수식으로 표현하면 다음과 같이 unit function으로 표현할 수 있다.

CDF의 성질

PDF의 성질
PDF는 다음과 같이 CDF를 미분한 꼴로 정의한다.

이 정의를 이용하여 위에서 봤던 예시에 대한 PDF 그래프와 식을 작성해보면 다음과 같다.

성질을 하나씩 살펴보자

이는 PDF가 단조증가함수임을 뜻한다.


이는 위에서 본 PDF와 CDF의 미분관계에 대한 성질이다.

이는 PDF 그래프의 밑면의 넓이가 1임을 뜻한다.
Discrete Random Variable의 CDF와 PDF의 일반형
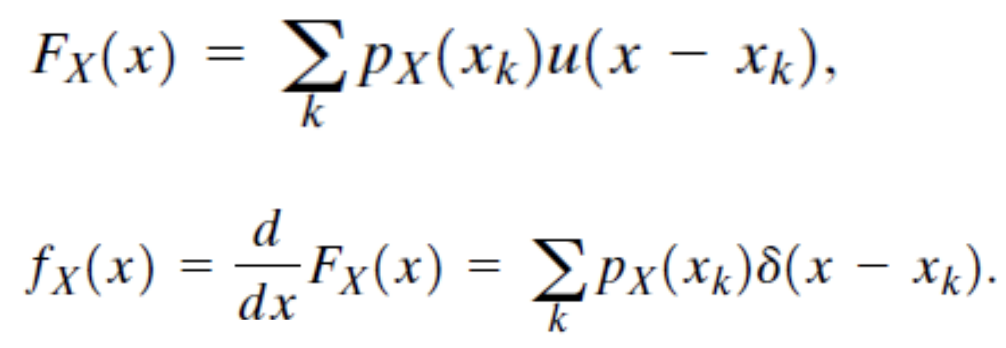
Discrete RV의 경우 정해진 일반형을 이용하여 분석할 수 있다.
조건부 CDF와 PDF

예시로 알아보자.
박스를 선택하고 공을 1개 꺼내는 경우에 대해서 보자.

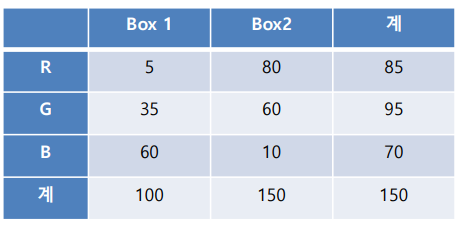


PDF에 대해 예시를 통해 좀더 살펴보자.

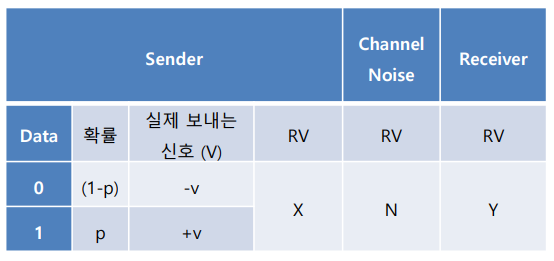
이때 noise N의가 Gaussian RV라면 식은 다음과 같이 된다. 그리고 이때 평균은 0이고 분산이 σ임을 알 수 있다.
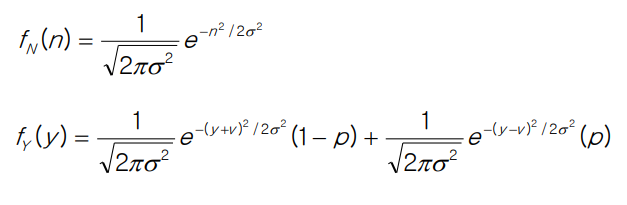
그리고 p=1/2인 경우를 그래프로 그리면 다음과 같다.
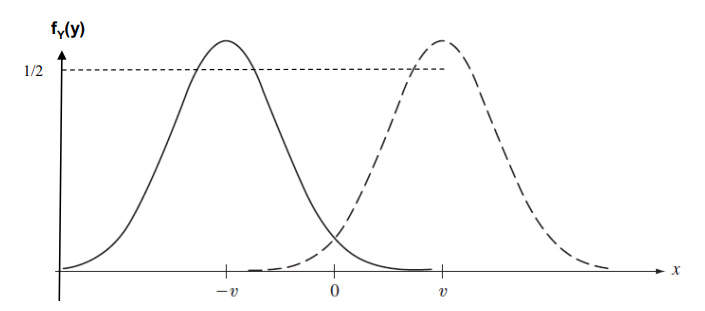
Sender가 0을 보냈을 때 receiver가 1이라 판단하여 받을 확률은 다음과 같다.
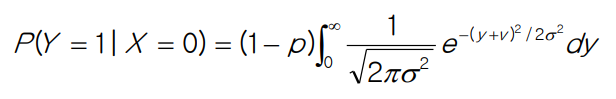
E[X]
Random Variable X의 평균을 구하는 방법에 대해 알아보자. 기본적인 식은 다음과 같이 rv와 그 확률의 곱을 적분하는 방식이다.

Uniform Random Variable의 평균은 다음과 같이 구한다.
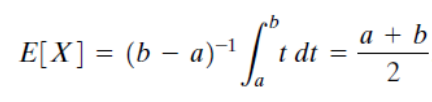
돗수분포표가 주어졌을 때 평균을 계산은 다음과 같다.

식을 보다 보면 특별한 상황에서의 대칭조건을 찾을 수 있다.


이번에는 Exponential Random Variable에서의 Mean값을 구하는 과정을 보자.
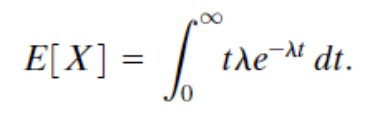

Y = g(X)의 평균을 구해보자.
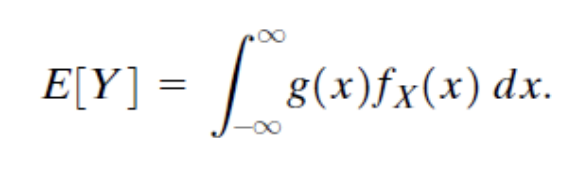
기본적인 식은 동일하다. 이번에는 discrete RV의 경우를 보자.
Discrete Random Variable Case

Variance of X
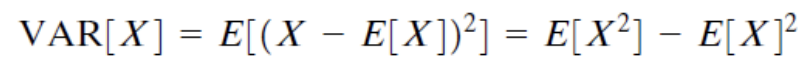
이를 가볍게 증명해보면 다음과 같다.

위의 식을 이용하여 아래의 성질들을 찾을 수 있다.
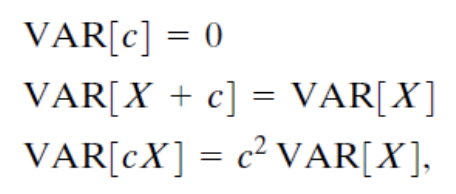
'Univ. Study > Probability and Random Variables' 카테고리의 다른 글
| Lecture 6 - Pairs of Random Variables(1) (0) | 2023.05.25 |
|---|---|
| Lecture 5 - Continuous Random Variables (0) | 2023.05.20 |
| Lecture3 - Discrete Random Variable (0) | 2023.04.14 |
| Lecture2 - Sequential experiments (0) | 2023.03.22 |
| Lecture1 - Basic Concepts of Probability Theory (0) | 2023.03.11 |



