Two Random Variables
확률변수가 여러개인 경우 아래와 같이 각각 축을 맡아서 pdf와 cdf를 표현하게 된다.

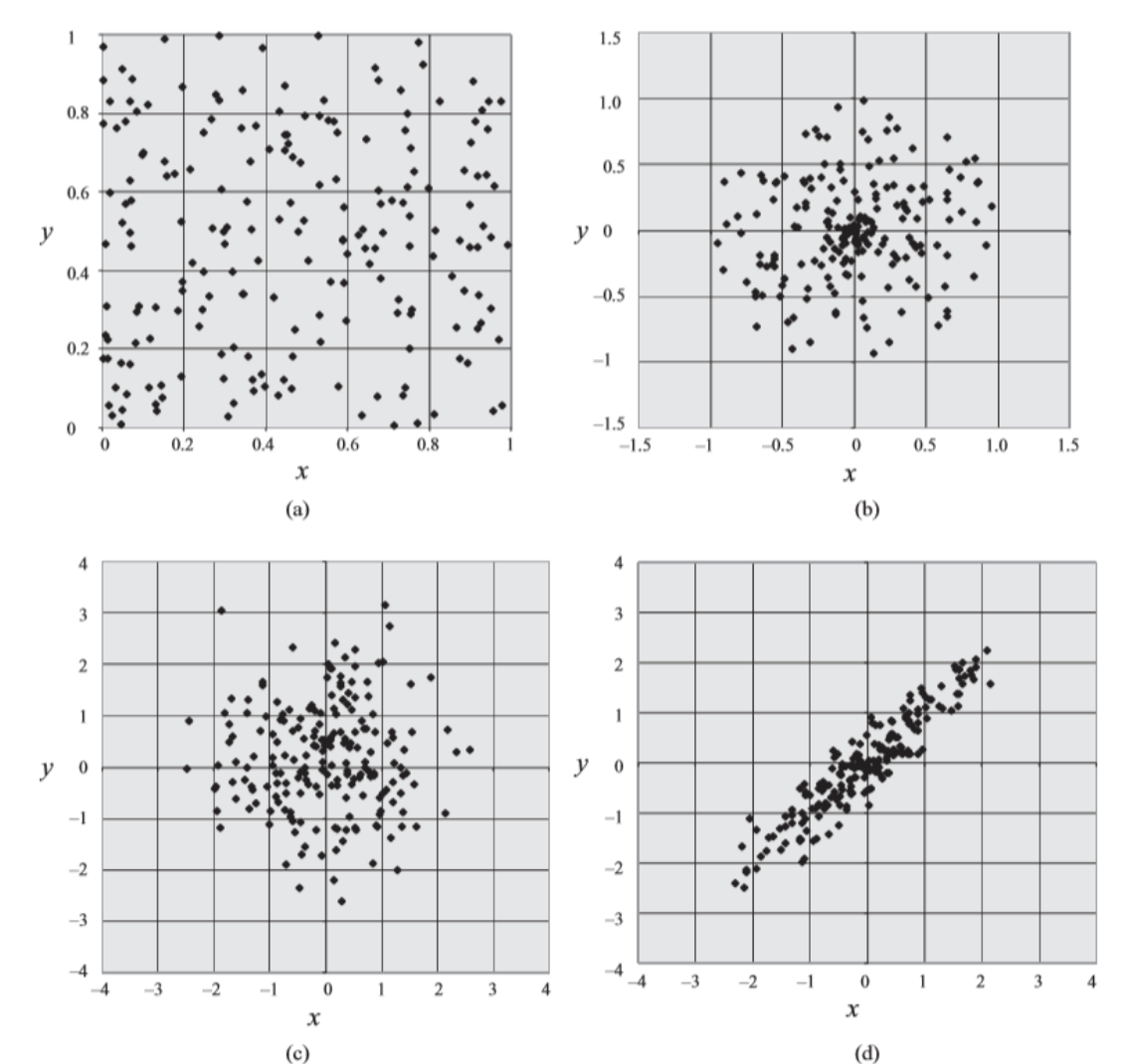
그런식으로 표현하면 위와 같이 두변수의 상관관계를 알아볼 수 있다.
Joint CDF of X and Y
X와 Y의 joint CDF를 그래프에 그리는 방식을 살펴보자.

이번엔 조금더 복잡한 예시를 통해 알아보자.
Sample space S가 (1,1), (2,1), (3,3) 3개의 원소로 구성된다고 했을 때 각 원소에 대한 확률은 아래와 같다. 이때의 joint CDF의 그래프를 그리고 식을 작성해보자.
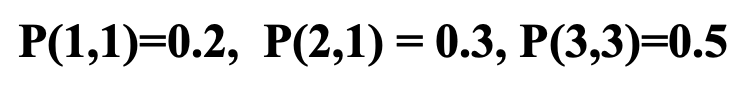
우선 식은 아래와 같이 작성할 수 있다.

그래프를 그리는 것이 조금 복잡할 수 있는데 이는 아래와 같이 생각할 수 있다.

이를 기반으로 그래프를 그리면 다음과 같다.

알아보기 조금힘들지만 느낌만 가져가도록 한다.
Joint CDF의 성질

세번째 성질은 아래와 같이 증명된다.

다섯번째 성질은 아래와 같이 증명된다.
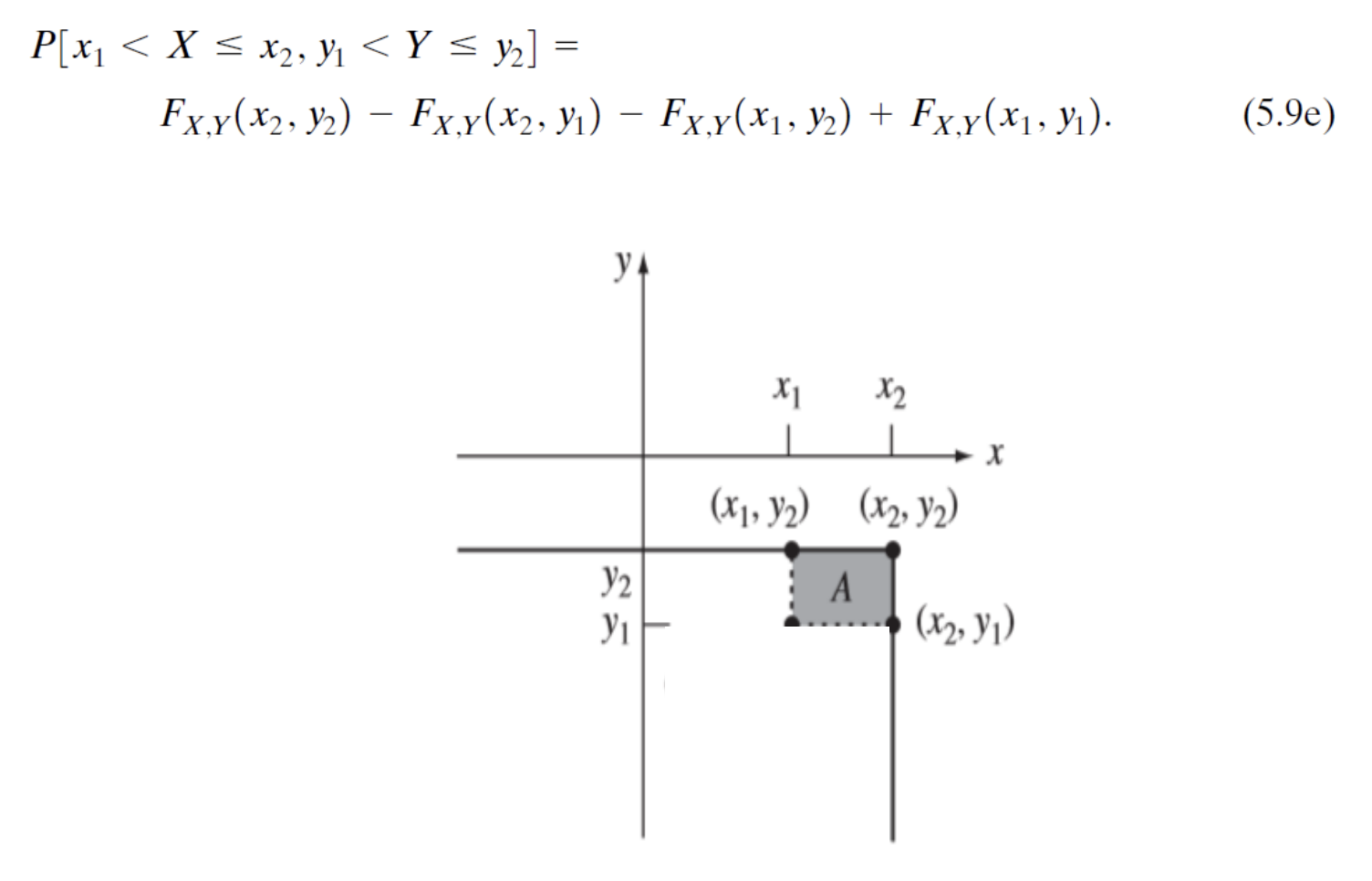
Continuous RV의 Joint PDF
이전에 다루었던 PDF의 성질과 같이 joint PDF도 미분을 통해 구할 수 있다.
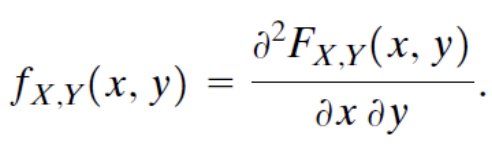
위에서 봤던 예시를 통해 PDF의 그래프와 식도 구해보면 아래와 같다.
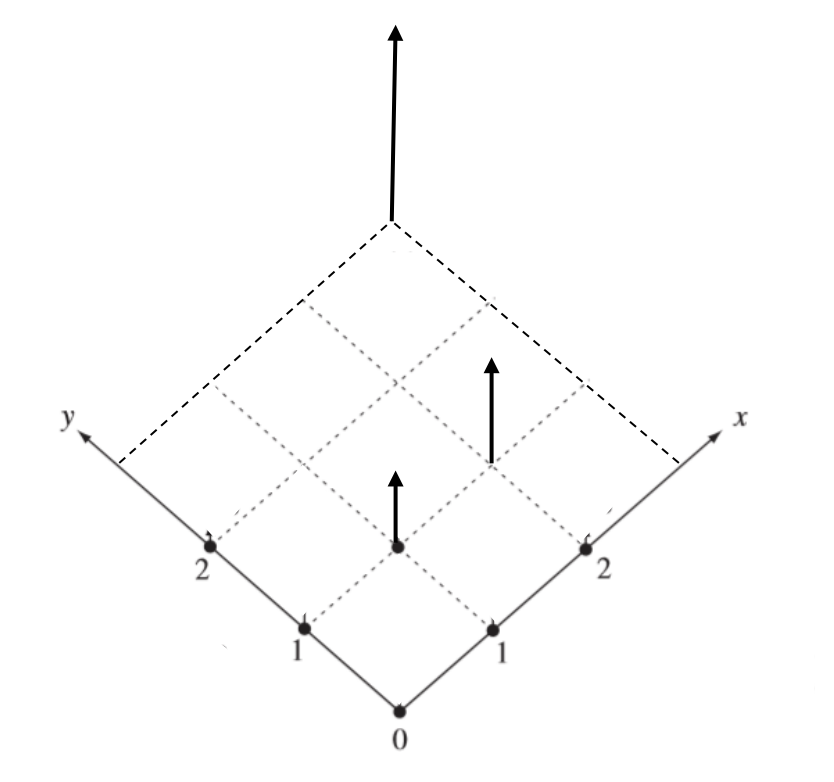

Joint PDF의 성질
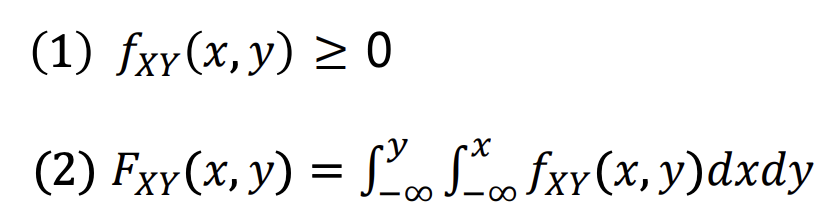




2번 성질은 아래와 같이 증명된다.

3번 성질은 아래와 같이 증명된다.

4번 성질은 아래와 같이 증명된다.

5번 성질은 아래와 같이 증면된다.

6번 성질은 아래와 같이 증명된다.

Discrete RV의 Joint CDF와 Joint PDF의 일반형
One Random Variable에서도 Discrete한 경우 CDF, PDF의 일반형이 있듯이 Two Random Variable에서도 존재한다.
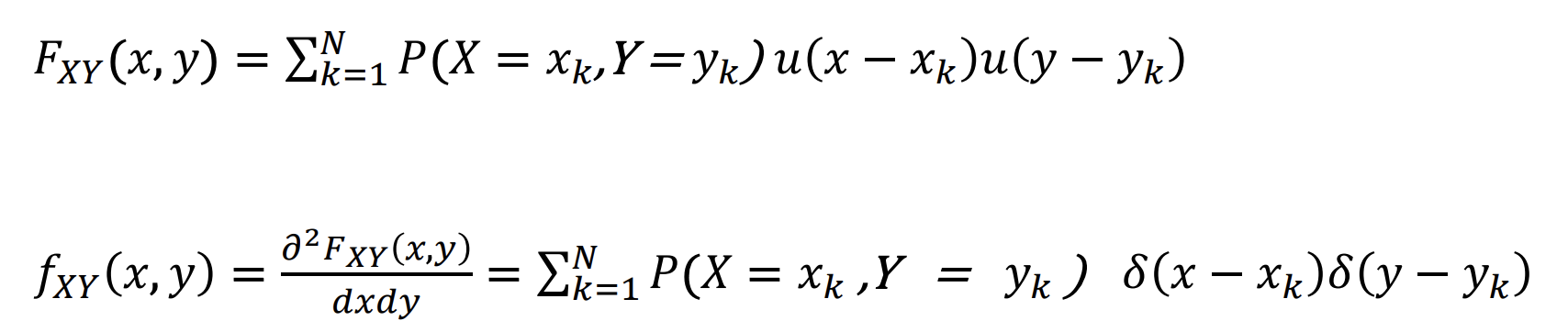
Independence of Two Random Variable
우선 두 Random Variable이 independent하다는 것은 아래의 정의를 만족한다는 것이다.

따라서 아래와 같이 CDF와 PDF의 경우에도 Joint식이 각각의 곱으로 표현된다.

'Univ. Study > Probability and Random Variables' 카테고리의 다른 글
| Lecture 8 - Vector Random Variables (0) | 2023.05.27 |
|---|---|
| Lecture 7 - Pairs of Random Variables(2) (0) | 2023.05.26 |
| Lecture 5 - Continuous Random Variables (0) | 2023.05.20 |
| Lecture 4 - One Random Variable (0) | 2023.05.13 |
| Lecture3 - Discrete Random Variable (0) | 2023.04.14 |



