Current and Current Density
전류(I)는 전하의 흐름으로, 단위 시간 동안에 흐른 전하의 양으로 정의된다.
전류밀도(J)는 단위면적당 전류의 양을 나타내는 것이다.


전류밀도에 대해서 좀더 생각해보면 아래와 같다.
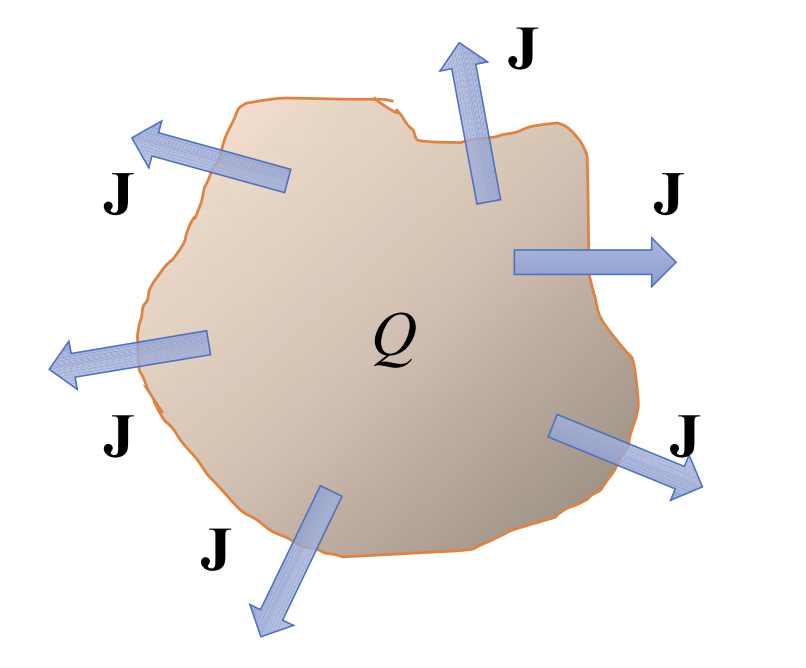
그림처럼 단위시간당 전류가 나가는 양이기 때문에 아래와 같이 식 계산이되고 정의를 보면 가우스 법칙과 유사한 느낌이 든다.

-가 붙는 이유는 전류가 '나가는' 양이기 때문에 줄어든다고 판단하여 음수가 되는 것이다.

Energy band structure in three material types
도체, 부도체, 반도체의 에너지 띠를 살펴보자.
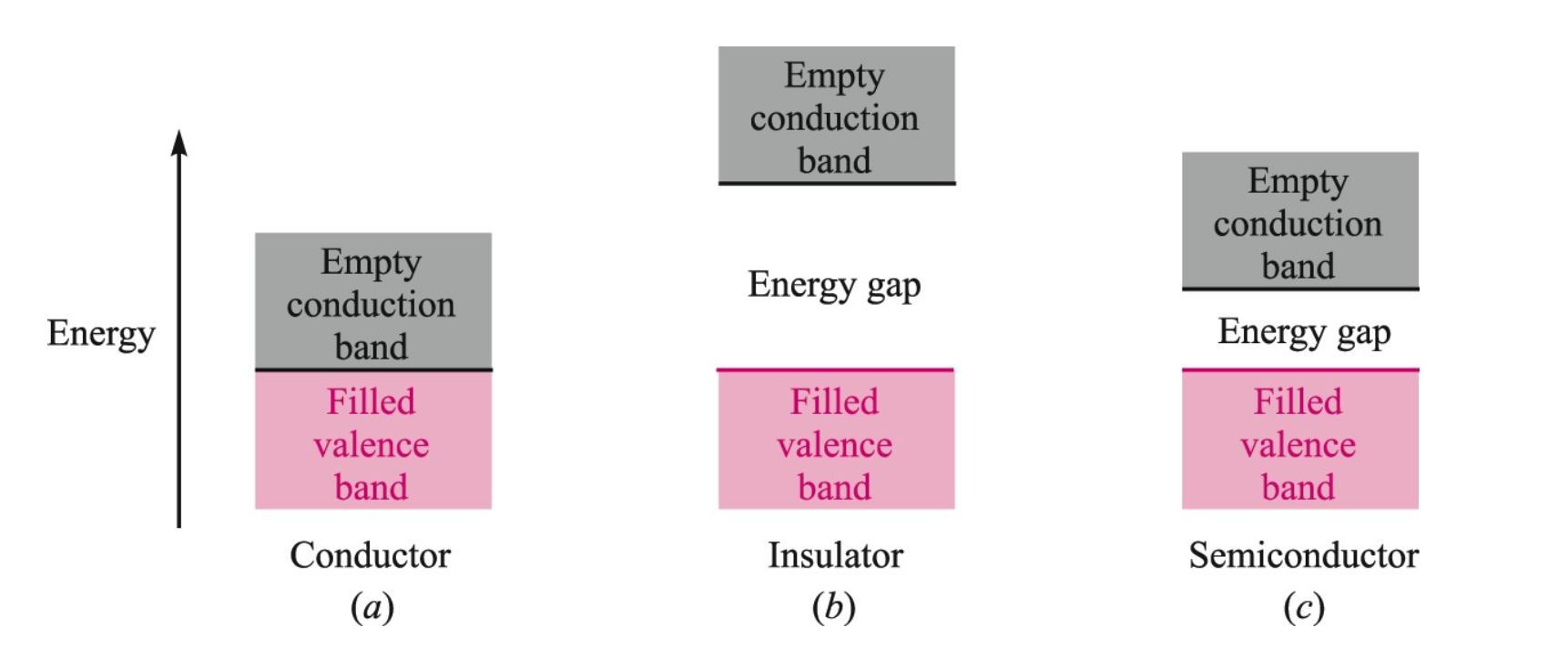
1. 도체는 원자 내 전자의 에너지 띠 간에 에너지 간격이 없어 전자가 자유롭게 움직인다.
2. 부도체는 큰 에너지 간격을 가지고 있어 전자를 전도대역으로 옮기기 위해서는 많은 에너지가 필요고 이러한 경우, 유전체가 파괴된다.
3. 반도체는 비교적 작은 에너지 간격을 가지고 있어 조금의 에너지(열, 빛 또는 전기장을 통해 가해진)로도 전자를 원자의 전도대역으로 이동시킬 수 있다.
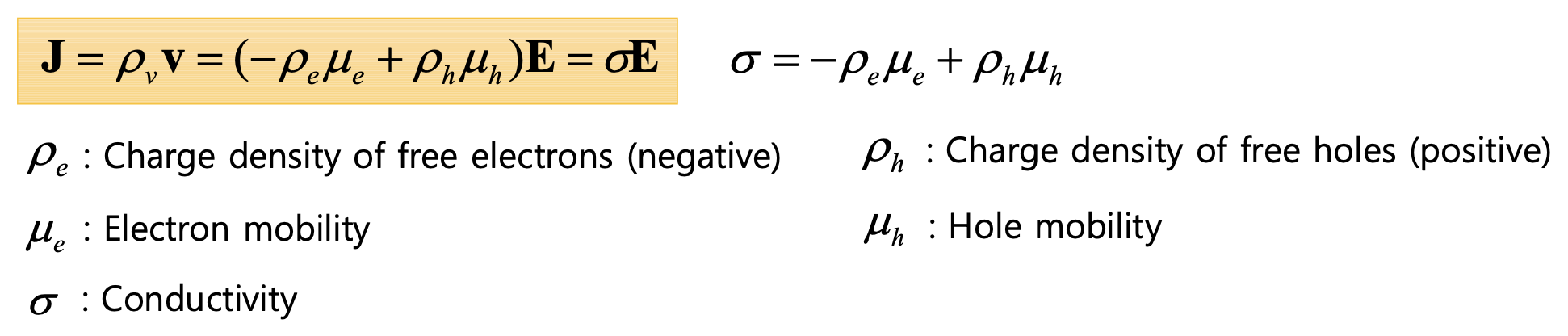
Resistance

전류 밀도에 관한 식에 아래 그림에서 찾을 수 있는 관계식들을 이용하면 옴의 법칙 V = IR을 도출할 수 있다.


또한 R=V/I에서 아래와 같은 식을 도출할 수 있다.
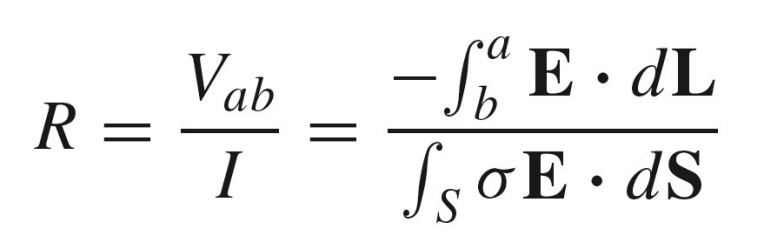
Electrostatic properties of Conductors
도체의 정전기적 특성에 대해서 알아보자. 우선 도체 내부의 전하들은 전부 도체의 경계로 몰린다.

이상적인 도체의 전도도는 무한하다. 따라서 아래와 같이 전하밀도가 0이 됨을 알 수 있다.
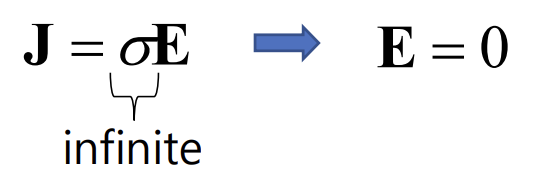

따라서 경계상황에서의 Electric field와 Electric flux density들을 따져보면 아래와 같다.

문제 풀이법
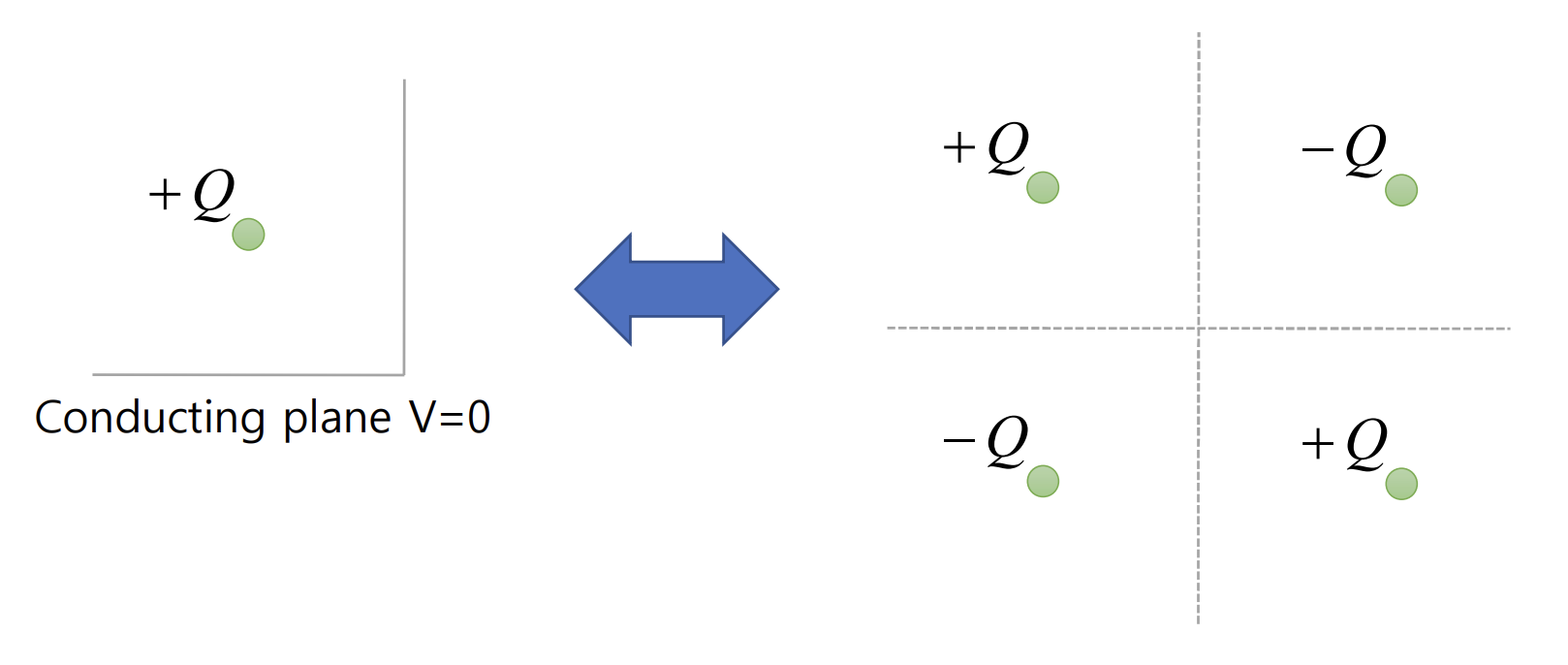
도체의 경우 전하가 존재하면 정확히 반대편에 같은 크기의 부호가 반대인 전하가 존재하는 것과 같은 효과가 있어서 아래와 같이 해석하여 문제풀이를 진행하면 간단하게 풀 수 있다.

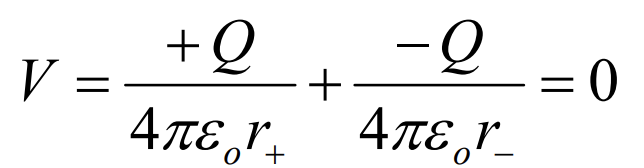
면이 두개인 경우 아래와 같이 세개의 가상 전하를 가정하고 문제풀이를 진행하면 된다.
선전하의 경우도 아래와 같이 똑같이 풀리는 것을 알 수 있다.

'Quality control (Univ. Study) > Electromagnetics' 카테고리의 다른 글
| Lecture 15 - Capacitance (0) | 2023.05.27 |
|---|---|
| Lecture 14 - Dielectrics (0) | 2023.05.26 |
| Lecture 12 - Energy and Potential(2) (0) | 2023.05.24 |
| Lecture 11 - Energy and Potential(1) (0) | 2023.05.16 |
| Lecture9, 10 - Gauss's Law, Divergence (0) | 2023.05.04 |



