Deep Sparse Rectifier Neural Networks
by Xavier Glorot et al. (2011)
https://proceedings.mlr.press/v15/glorot11a/glorot11a.pdf
-요약-
이 논문은 깊은 희소 Rectifier 신경망 구조를 소개하고 검증한다. 그 결과, Sparse rectifier neural network는 기존의 깊은 신경망보다 더 높은 성능을 보여주고, 제안된 구조의 효과가 입증되었다는 것을 보여준다.
논문의 핵심은 Rectifier 활성화 함수와 희소 정규화를 결합함으로써, 기존의 Deep neural network보다 더 높은 성능과 이해하기 쉬운 구조를 제공하는 것이다.
Sigmoid neuron이 hyperbolic tangent neuron보다 생물학적 타당성이 더 높지만 hyperbolic tangent neuron은 multi-layer neural network에서 더 좋다.
이 논문에서는 rectifying neuron이 0에서 비선형적이고 미분불가능해서 실제 0에서 희소 표현이 됨에도 hyperbolic tangent neuron 보다 더 좋거나 같은 성능을 갖고 있고 데이터가 부족한 상황에 굉장히 적합함을 보인다.
추가적인 unlabeled data가 있는 semi-supervised setup을 통해 이점을 가져갈 수 있지만 deep rectifier network는 거대한 labeled dataset으로 구성된 purely supervised task에 unsupervised pre-training이 전혀 없이도 최선의 결과를 낼 수 있다.
Background
Semi-supervised learning
Semi-supervised learning은 supervised learning의 한계를 극복하는 방법중 하나이다. 우선 supervised learning의 한계를 알아보자. Supervised learning은 딥러닝의 가장 대표적인 방법중 하나이지만 학습시켜주는 데이터의 패턴을 외우는 학습법에 불과하다고 볼 수 있다. 따라서 한번도 보지 않은 데이터에 대해서는 정확도가 떨어질 수 있다. 따라서 성능을 높이기 위해서는 방대한 양의 labeled data가 요구된다. 하지만 labeled data는 상황에 따라 충분한 양을 얻기 힘들 수 있다. 그러한 경우 supervised learning의 치명적인 단점이 나타난다.
이러한 한계를 극복하기 위해 semi-supervised learning이 제안되었다. 이름에서 알 수 있듯이 적은 양의 labeled data와 대용량의 unlabeled data를 이용하는 것이다. Labeled data에는 supervisdded learning을 적용하고 unlabeled data에는 unsupervised learning을 적용하여 성능향상을 도모하는 것이다.

Semi-supervised learning에 대한 상세한 내용은 추후에 다시 다루도록하고 우선은 기본적인 내용만 훑어다.
Advantages of Sparsity
해당 논문에서 rectifying non-linearity 를 이용하는것이 희소표현에서 이점을 갖는 것을 보일 것이다. 그리고 컴퓨터 공학적인 관점에서 그러한 표현이 이점이 있음을 다음의 이유를 통해 알 수 있다.
Information disentangling (정보가 얽히지 않음)
주로 밀도가 높은 data가 있으면 작은 변화만으로도 data가 얽혀서 해석하기 굉장히 어려워지는 경향이 있는데 sparse representation은 복잡성이 낮아 얽힘 현상이 적다.
Efficient variable-size representation (효율적으로 가변적인 표현가능)
Input이 다르면 정보의 양도 달라지기 때문에 가변적인 데이타 구조를 이용하는 것은 흔한 일이다.
활성 뉴런의 수의 가변성은 모델이 효율적인 차원의 표현과 높은 정확도를 가지게 된다.
Linear separability (선형 분리성)
Text-related application에서 data는 굉장히 sparse하다. 이때 sparse representations들은 선형적으로 분리가 가능해서 유연성이 높다.
Distributed but sparse
Dense distributed representations는 pure local representations에 비해 잠재적으로 기하급수적으로 효율적이다.
Sparse representation은 여전히 기하급수적으로 효율적이다. 기준들에 따르면 좋은 교환(trade-off)으로 보인다.
Deep rectifier network
Rectifier Neurons
뇌의 cortical neuron에서 사용되는 활성화 함수가 rectifier function으로 근사화될 수 있다. Rectifier function은 한쪽 방향으로만 효과를 나타내기 때문에, 입력 패턴에 대한 반응이 대칭 또는 반대칭이 나타나지 않는다. 이때 논문에서는 두 개의 rectifier unit을 결합함으로써 대칭 또는 반대칭을 얻을 수 있다고 제안합니다. 이전에 발표된 rectifying activation functions in recurrent neural networks에 관한 연구를 참조한다.
Advantage
Rectifier 함수는 희소 표현을 가능하게 한다. 이 희소성은 경사 흐름의 용이성과 계산에 자원이 적게 드는 등의 수학적 이점을 가져온다. 논문에서는 model을 parameter를 공유하는 linear 모델의 조합으로 관찰하고 있어, 수학적 고찰이 용이하고 계산량이 줄어든다.

Potential Problem
0에서의 hard saturation이 신경망 최적화에 부정적인 영향을 끼칠 수 있다. Rectifier 활성화 함수와 그것의 soft한 버전인 softplus를 테스트를 하여 gradient가 어떤 경로를 따라 propagate될 수 있고, 숨겨진 유닛들이 모두 0이 아닐 경우 strong 0이 supervised training에 도움이 된다는 것을 알 수 있다. 또한 숫자 문제를 방지하고 sparsity를 증가시키기 위해 활성화 값에 L1 패널티를 사용합니다. 추가적으로 rectifier netwark에는 scaling 문제가 있을 수 있고 이것은 매개변수에 언바운드 문제를 일으킬 수 있다.
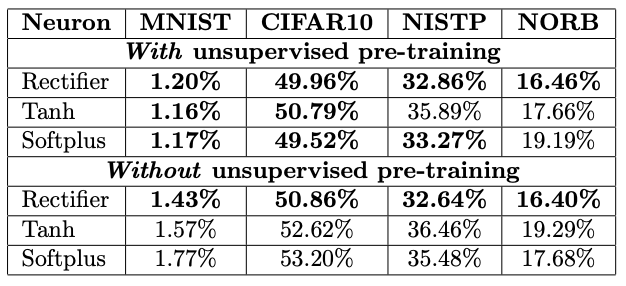

What have I learned
논문을 완전히 이해할 지식과 능력도 없어서 몇단락 읽다가 포기할까하다가 배경지식 쌓는 것에 의미를 두기 위해서 이곳 저곳 조사해가며 Rectifier Neural Network의 장점에 대해서 알게 되었고 어째서 model을 만드는 과정에서 rectifier activation function이 적극적으로 쓰이는지에 대해서 조금이나마 이해 할 수 있는 기회였다.
영어에 대한 두려움이 없었는데 생소한 내용이 전부 영어로 복잡하게 쓰여있어서 없던 두려움이 생길 정도였다...
다음에 도전할 논문은 국문 버전으로 살펴보고자 한다.
'Drawing (AI) > Paper review' 카테고리의 다른 글
| BERT(1) (0) | 2023.08.02 |
|---|---|
| [논문 리뷰] Attention is all you need (2) (0) | 2023.07.25 |
| [논문 리뷰] Attention is all you need(1) (1) | 2023.07.19 |
| [논문 리뷰] AutoRec: Autoencoders Meet Collaborative Filtering (0) | 2023.07.10 |
| [논문 리뷰] Long Short-Term Memory (0) | 2023.03.12 |



