Attention is all you need
NIPS 2017
기존에 SOTA를 달성하였던 Seq2Seq보다 뛰어난 성능으로 인공지능 학계를 뒤집은 Transformer가 데뷔한 논문이다. 현재는 vision분야에서도 ViT(Vision Transformer)라는 이름으로 이용되고 있다. 가장 최근에 얀르쿤이 공동저자로 참여하여 Meta에서 발표한 논문에서도 ViT를 이용하였다.
Background
Seq2Seq
Sequence-to-Sequence는 아래와 같이인코더와 디코더라는 두 개의 모듈로 구성된다. 인코더는 입력 문장의 모든 단어들을 순차적으로 입력받은 뒤에 마지막에 이 모든 단어 정보들을 압축해서 하나의 벡터로 만드는데, 이를 컨텍스트 벡터(context vector)라고 한다. 입력 문장의 정보가 하나의 컨텍스트 벡터로 모두 압축되면 인코더는 컨텍스트 벡터를 디코더로 전송한다. 디코더는 컨텍스트 벡터를 받아서 번역된 단어를 한 개씩 순차적으로 출력한다.

인코더 셀은 모든 단어를 입력받은 뒤에 인코더 셀의 마지막 시점의 hidden state를 디코더 셀로 넘겨주는데 이 부분을 context vector라고 한다.
이때 context vector가 encoder의 모든 시퀀스 정보를 포함하기 때문에 decoding시에 개별 토큰과의 관계 파악이 어렵고 Sequence가 길어지면 Gradient vanishing 위험이 존재한다는 문제가 있어서 Attention Mechanism을 이용하기 시작했다.
Attention
Attention은 Transformer의 핵심 개념이다. 다양한 종류의 attention mechanism이 있지만 우선 가장 간단한 dot-product attention을 통해 알아보고자 한다.

Seq2Seq과는 다르게 Attention에서는 인코더에서의 hidden state를 모두 행렬 형태로 저장을 해둔다.

그후에는 위와 같이 해당 hidden state 행렬을 디코더의 hidden state값과 곱하여 나온 Alignment Scores를 softmax함수에 태워서 Attention Weights를 구한다. 이때 Attention Weight는 합이 1인 가중치 값이다.

구한 Attention Weights를 hidden state 행렬에 곱하고 더하여 Weighted Sum을 구하면 그 값이 Attention Score가 된다.

여기서는 해당 Attention Score를 concat을 하여 아래와 같이 dh2를 예측을 한다.

Transformer Training Architecture
아래는 눈문에서 제공하는 Transformer의 구조이다.

위에 그림에서 볼 수 있듯이 크게 input to encoder, encoder, decoder, last layer로 나누어 볼 수 있다.
Encoder
우선 Input to encoder파트를 먼저 보자.
해당 부분에서는 문장의 각 시퀀스(토큰)를 학습에 사용되는 벡터로 임베딩하는 embedding layer를 구축하고 임베딩 행렬 W에서 look-up을 수행하여 해당하는 벡터를 반환한다. 해당 부분을 파이토치로 구현한 유명한 깃허브의 코드를 참고하면 아래와 같다.(https://github.com/jadore801120/attention-is-all-you-need-pytorch/tree/master)
class Encoder(nn.Module):
''' A encoder model with self attention mechanism. '''
def __init__(
self, n_src_vocab, d_word_vec, n_layers, n_head, d_k, d_v,
d_model, d_inner, pad_idx, dropout=0.1, n_position=200, scale_emb=False):
super().__init__()
self.src_word_emb = nn.Embedding(n_src_vocab, d_word_vec, padding_idx=pad_idx)
self.position_enc = PositionalEncoding(d_word_vec, n_position=n_position)
self.dropout = nn.Dropout(p=dropout)
self.layer_stack = nn.ModuleList([
EncoderLayer(d_model, d_inner, n_head, d_k, d_v, dropout=dropout)
for _ in range(n_layers)])
self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)
self.scale_emb = scale_emb
self.d_model = d_model이때 encoding 부분은 아래와 같이 seq2seq과 다르게 순서와 관계없이 동시에 parallel하게 임베딩된 벡터가 인코더에 입력되기 때문에 그 순서 정보를 따로 보전하여 정보를 전달해야한다.
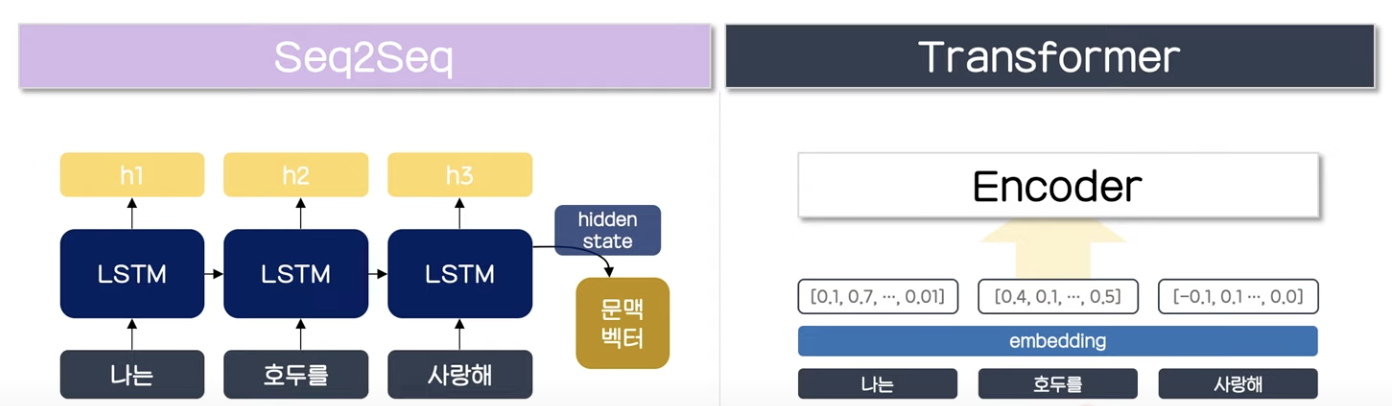
아래는 기본적인 input embedding 과정을 알아보기 쉽게 표현한 그림이다.
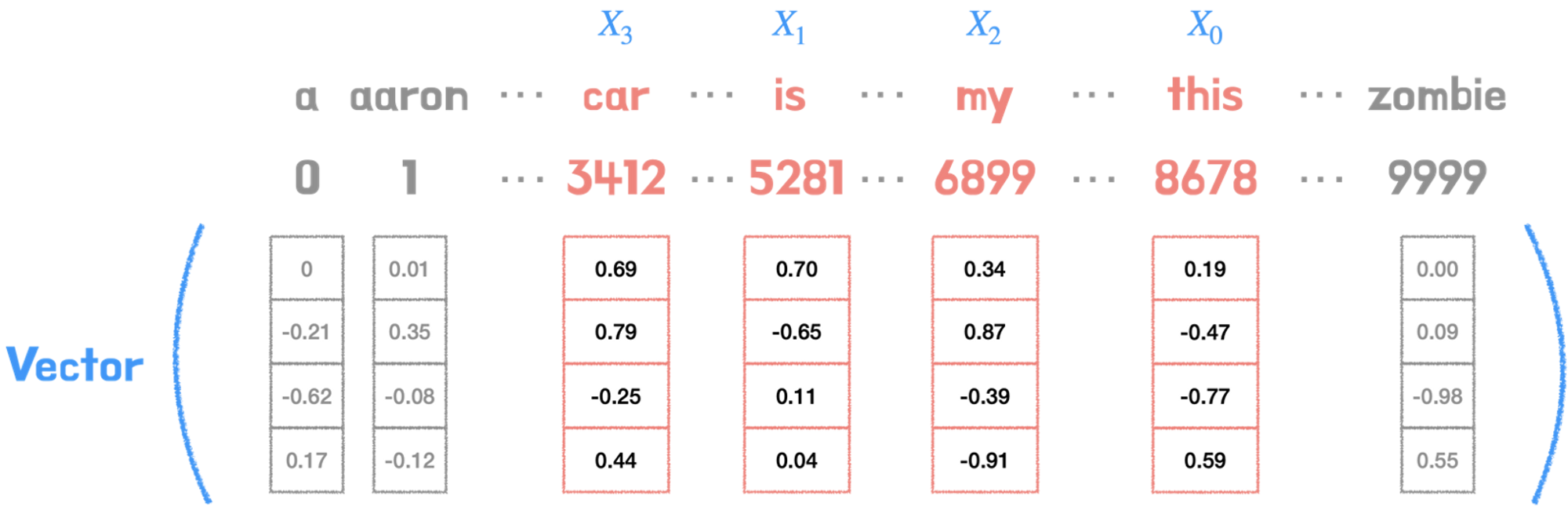
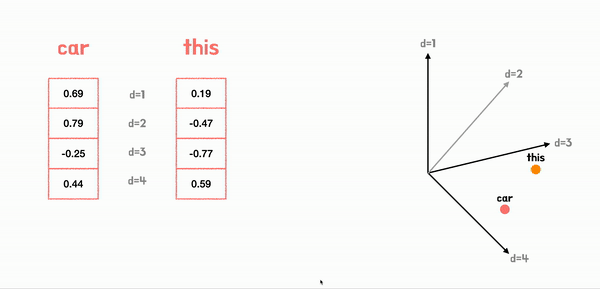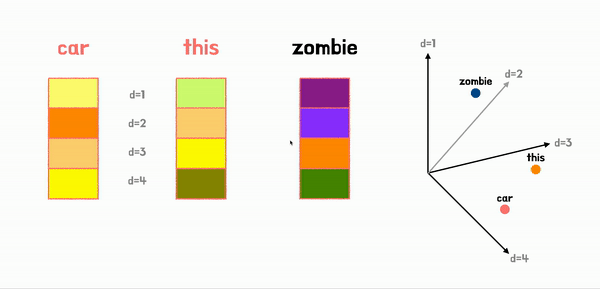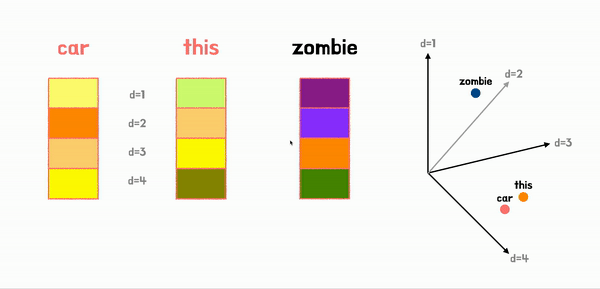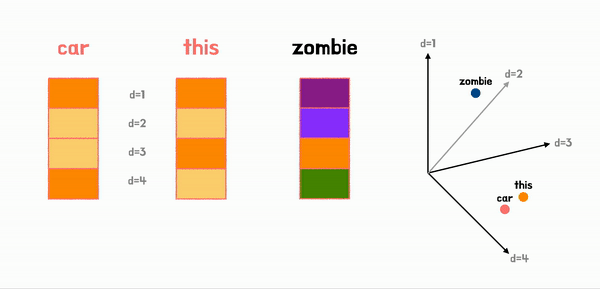
Positional Encoding이라는 방법을 이용해서 토큰의 순서 정보를 담아서 encoder에 입력해준다.
class PositionalEncoding(nn.Module):
def __init__(self, d_hid, n_position=200):
super(PositionalEncoding, self).__init__()
# Not a parameter
self.register_buffer('pos_table', self._get_sinusoid_encoding_table(n_position, d_hid))
def _get_sinusoid_encoding_table(self, n_position, d_hid):
''' Sinusoid position encoding table '''
# TODO: make it with torch instead of numpy
def get_position_angle_vec(position):
return [position / np.power(10000, 2 * (hid_j // 2) / d_hid) for hid_j in range(d_hid)]
sinusoid_table = np.array([get_position_angle_vec(pos_i) for pos_i in range(n_position)])
sinusoid_table[:, 0::2] = np.sin(sinusoid_table[:, 0::2]) # dim 2i
sinusoid_table[:, 1::2] = np.cos(sinusoid_table[:, 1::2]) # dim 2i+1
return torch.FloatTensor(sinusoid_table).unsqueeze(0)
def forward(self, x):
return x + self.pos_table[:, :x.size(1)].clone().detach()위의 코드와 설명에서 알 수 있듯이 단순히 embedding vector에 positional 정보를 더해서 encoder에 input해줄 준비를 하는 것이다.

이때 Positional encoding 값들은 아래와 같은 사인, 코사인 함수이다.
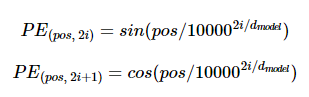
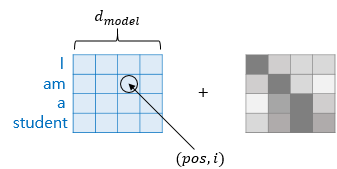
pos는 입력 문장에서의 임베딩 벡터의 위치를 나타내며, i는 임베딩 벡터 내의 차원의 인덱스를 의미한다. 위의 식에 따르면 임베딩 벡터 내의 각 차원의 인덱스가 짝수인 경우에는 사인 함수의 값을 사용하고 홀수인 경우에는 코사인 함수의 값을 사용한다. 또한 위의 식에서 d model은 트랜스포머의 모든 층의 출력 차원을 의미하는 트랜스포머의 하이퍼파라미터이다. 임베딩 벡터 또한 d model의 차원을 가지는데 위의 그림에서는 마치 4로 표현되었지만 실제 논문에서는 512의 값을 가진다.
50 × 128의 크기를 가지는 포지셔널 인코딩 행렬을 시각화하여 어떤 형태를 가지는지 확인해보자.
# 문장의 길이 50, 임베딩 벡터의 차원 128
sample_pos_encoding = PositionalEncoding(50, 128)
plt.pcolormesh(sample_pos_encoding.pos_encoding.numpy()[0], cmap='RdBu')
plt.xlabel('Depth')
plt.xlim((0, 128))
plt.ylabel('Position')
plt.colorbar()
plt.show()
#(1, 50, 128)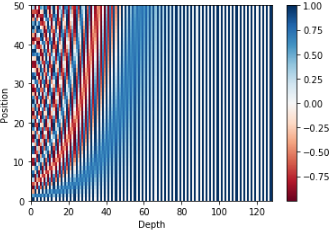
토큰 간의 거리를 포현한 것이라고 보면된다.

Multi-Head Self Attention
Query, Key, Value라는 개념을 이용하여 설명을 하고 있다. 우선 Query는 '던져주는 값', 검색어에 해당하는 개념이고 해당 Query의 값을 기준으로 찾는 대상이 Key가 될 것이고 Key가 갖고 있는 실제 값이 Value이다.

위의 그림에서 설명을 해보자면 Query와 가장 유사한 key는 Key2이다. 이때 전체 Key중 Query에 대해 각 key들이 지니는 유사도를 계산하면 [a1,a2,a3,a4]가 되고 그 유사도를 가중치로 이용한다. 가중합을 구하기 위해 an*Value를 계산하면 a1[0.1, 0.5] + a2[-0.1, 0.7] + a3[-0.9, 0.1] + a4[0.0, -0.8]이 된다. 이 계산 결과는 결국 Query와 가장 관련이 깊은 Key의 Value를 위주로 모든 값을 가져오게 된다. 이러한 과정을 Attention이라고 한다.
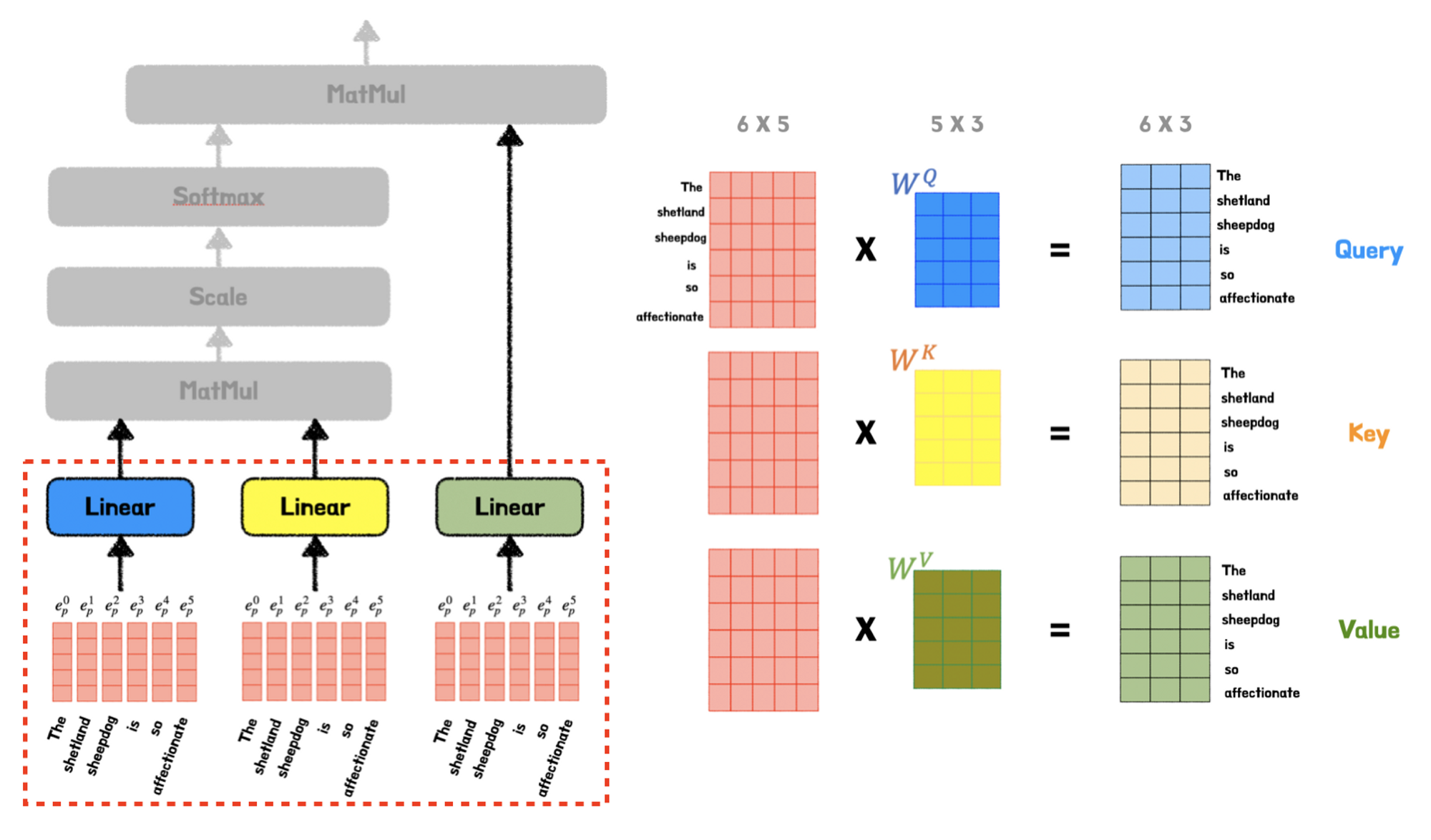
위와 같이 똑같은 내용을 세번 copy하여 각각 다른 가중치를 곱해주어 Query, Key Value역할을 부여하고 식의 input으로 작동한다.

이때 Attention Score는 아래와 같이 query와 key 행렬곱으로 나타내 진다. 행렬곱은 행렬 간의 유사도를 의미하기에 Attention Score는 query와 key의 유사도 행렬을 의미한다.
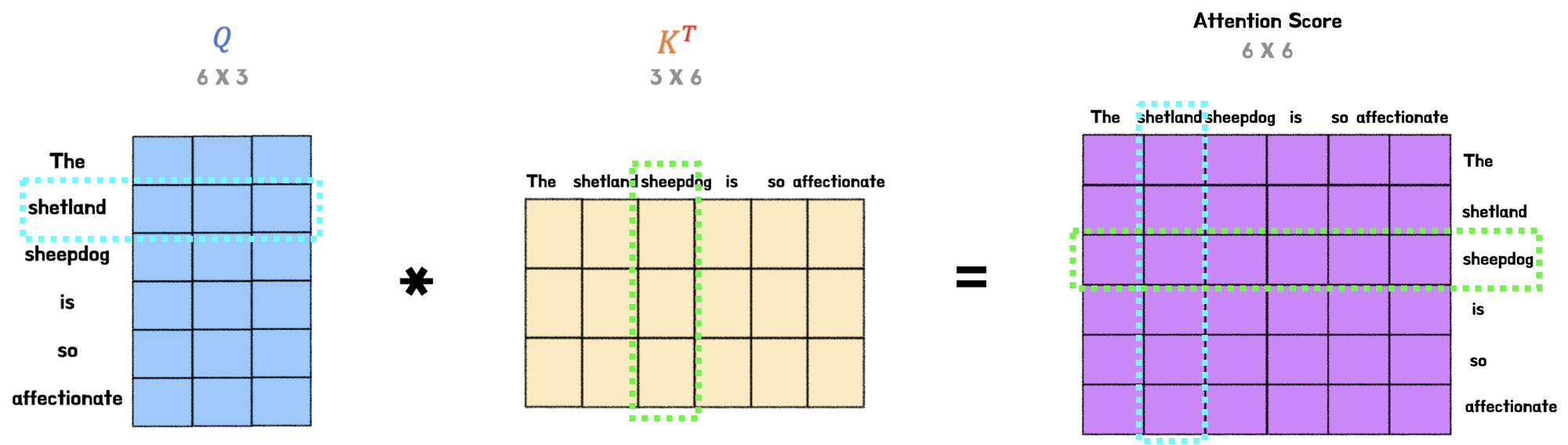
이제 Multi-head Attention은 병렬의 개념을 이용하는 것이다. 간단하게 그림으로 보면 아래와 같다.
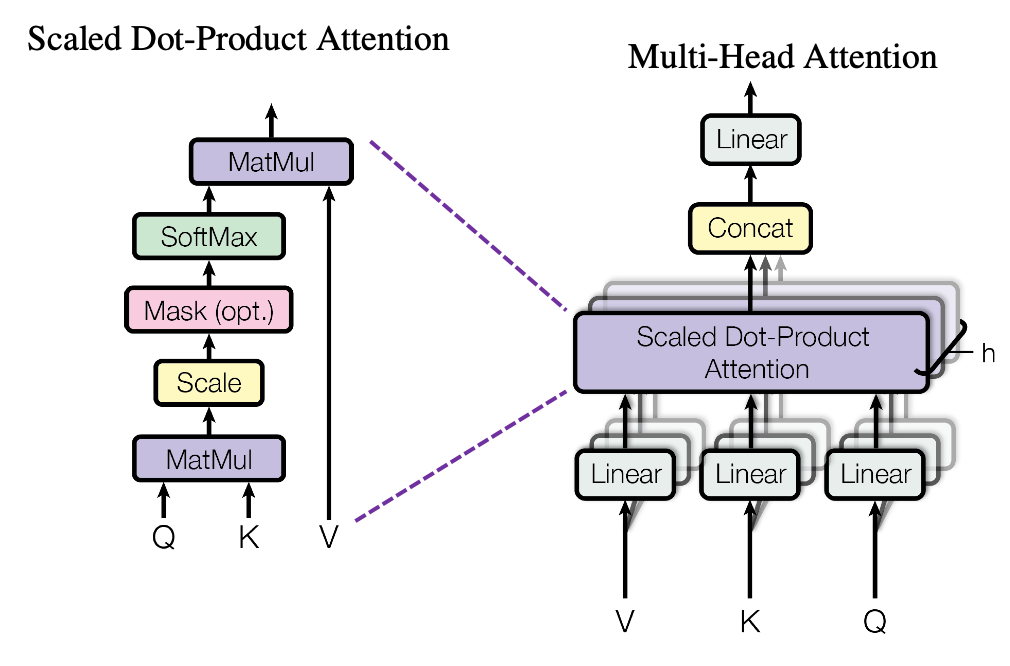
이를 텐서 단위로 좀 자세히 보면 아래와 같다.
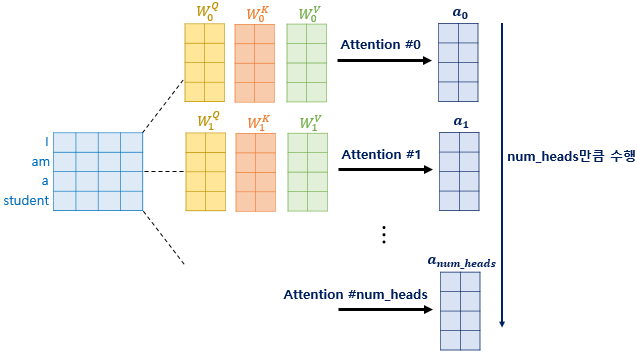
한 덩어리였던 Query, Key, Value를 설정해준 num_heads에 따라서 몇갈래으로 병렬 연산을 할지 결정하게 된다.
그런식으로 num_heads만큼 attention score를 구하고 concat을 해주면 Encoder의 input과 동일한 크기의 tensor가 나온다.
그렇다면 왜 이런식으로 병렬 연산을 진행할까?
그 이유는 앙상블 학습에서 추론해볼 수 있다. 똑같은 모델을 여러개 concat하여 병렬적으로 학습을 시키면 각기 다른 지점에 가중치를 두고 학습을 진행한다. 따라서 더욱 풍부한 의미 관계를 담고 있는 결과를 낼 수 있는 것이다. 이를 통해 다양한 case의 task에 대해서 적절하게 수행할 수 있는 모델이 완성되는 것이다.
Feed Forward Network
Feed Forward Network에 해당하는 레이어는 아래와 같은 방식으로 계산된다.
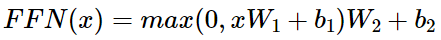
이는 간단히 말해서 두개의 Fully Connected Layer를 쌓고 ReLU를 activation function으로 이용하는 것이다.
이를 간단하게 코드로 구현해보면 아래와 같다.
import tensorflow as tf
def point_wise_feed_forward_network(d_model, dff):
return tf.keras.Sequential([
tf.keras.layers.Dense(dff, activation='relu'), # (batch_size, seq_len, dff)
tf.keras.layers.Dense(d_model) # (batch_size, seq_len, d_model)
])
d_model = 128
dff = 512
batch_size = 64
input_seq_len = 37
sample_input = tf.ones((batch_size, input_seq_len, d_model))
print(sample_input.shape)
sample_ffn = point_wise_feed_forward_network(d_model, dff)
sample_ffn.build(sample_input.shape)
sample_ffn.summary()그리고 해당 내용을 그림으로 살펴보면 아래와 같다.
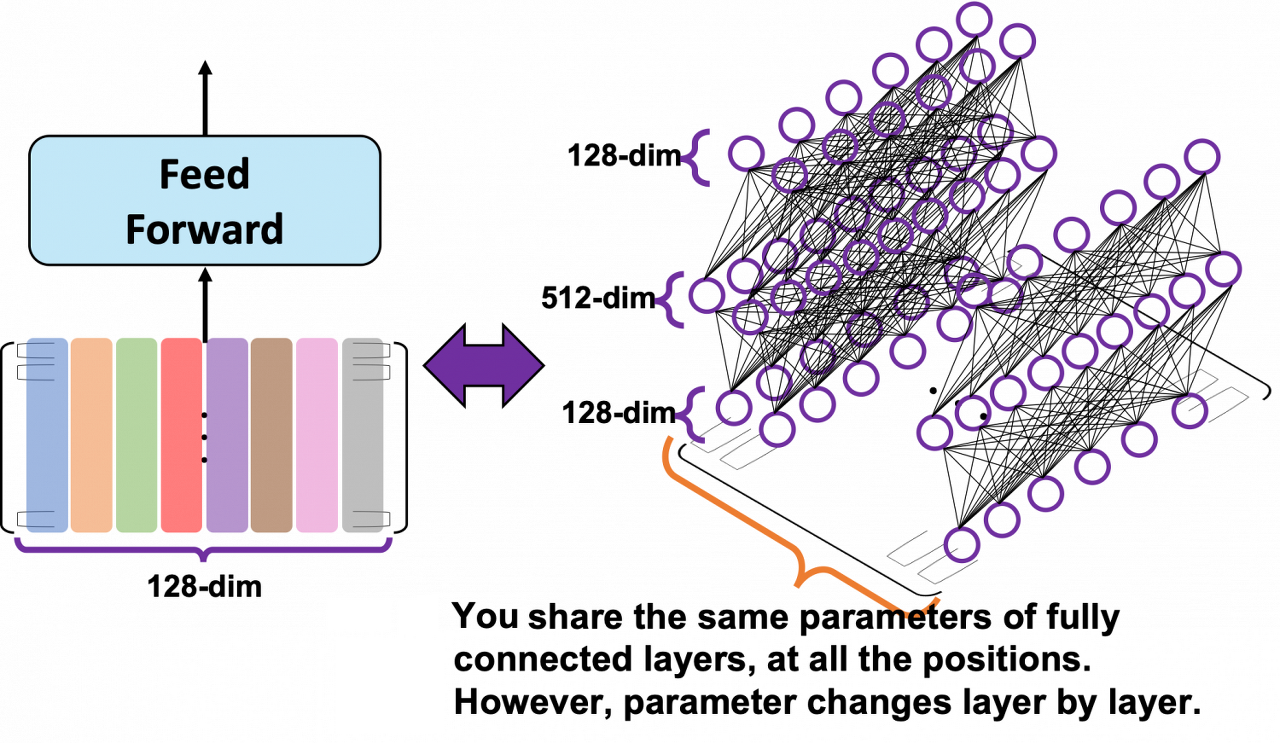
Position-wise 피드포워드 신경망의 매개변수 수를 보면 문장의 모든 위치에서 동일한 매개변수를 공유하고 있음을 알 수 있다. 즉, 위의 그림에서 단일 레이어의 모든 위치에서 동일한 조밀하게 연결된 레이어를 사용한다는 의미입니다. 그러나 position-wise 피드포워드 네트워크의 매개변수는 계층마다 변경된다.
Residual Connection/Layer Norm
앞에서 본 과정들을 거치면 아래의 노란색 tensor 값을 얻게 되는데 이때 해당 값을 Input tensor와 더하여 연두색 tensor를 만든다.
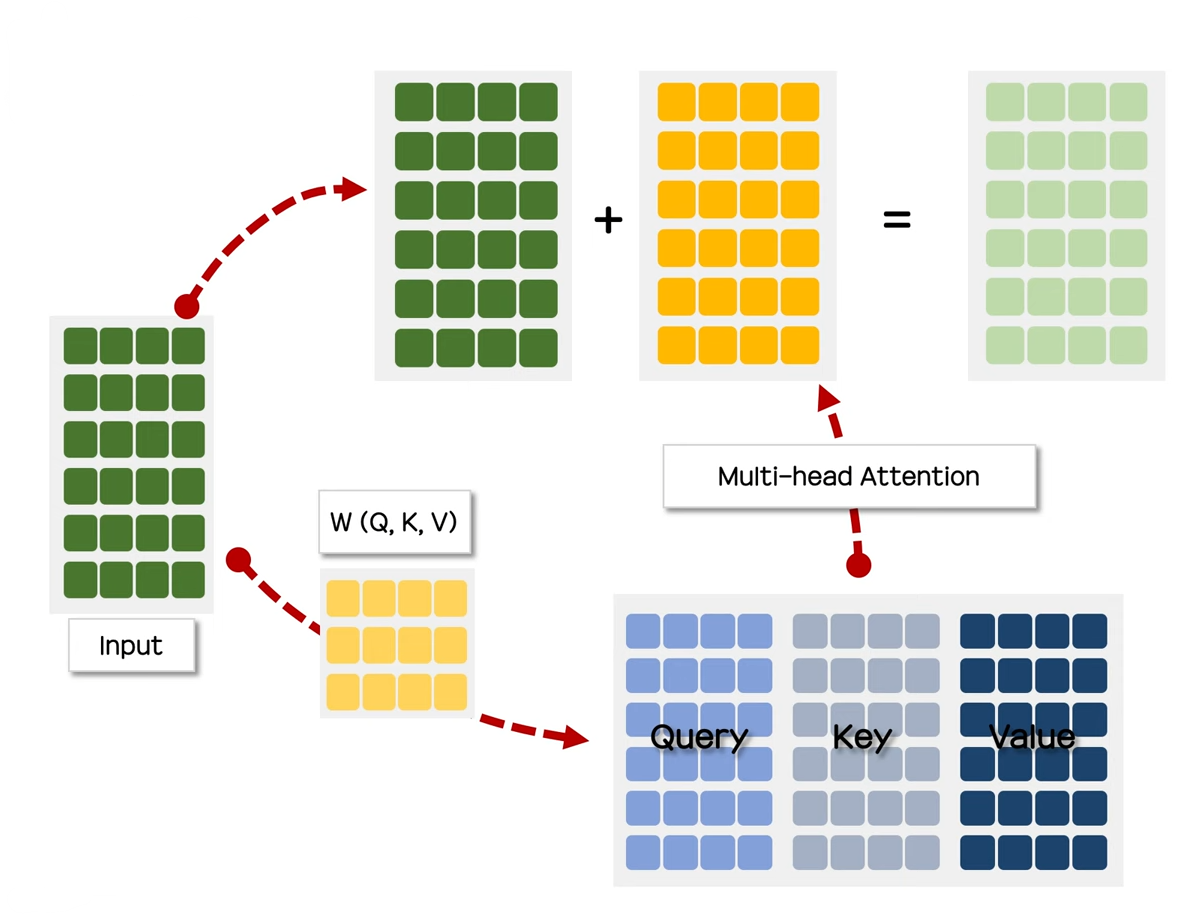
이제 해당 레이어에 layer normalization을 적용한다.
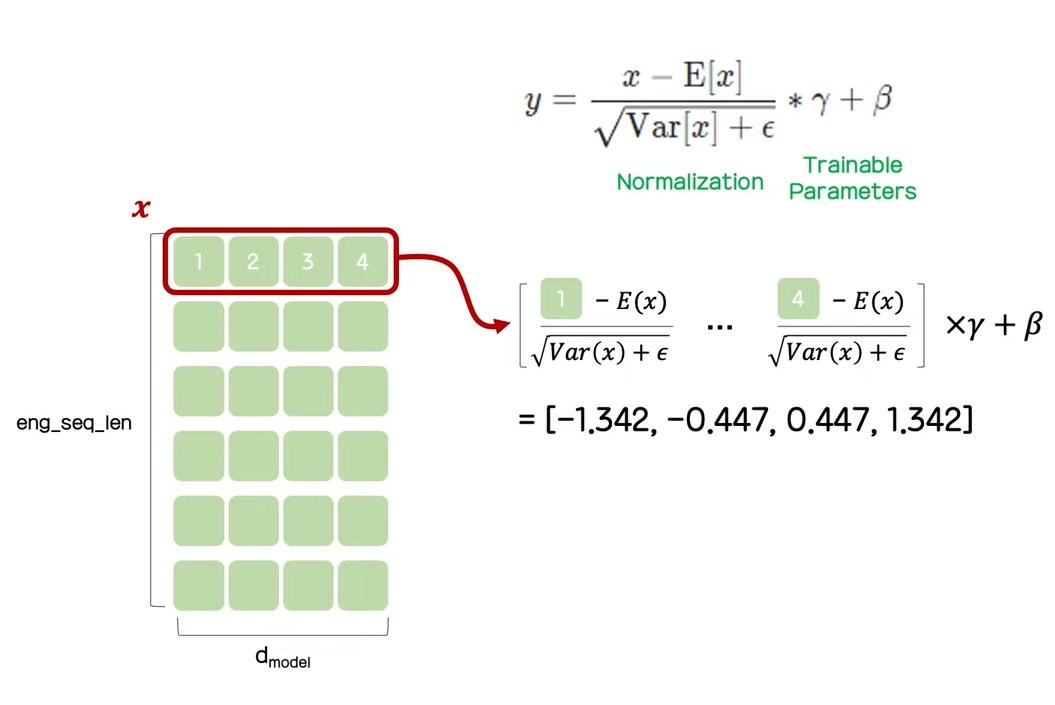
Layer normalization은 위와 같이 마지막 열에 대해서 적용하여 결과를 내는 것이다.
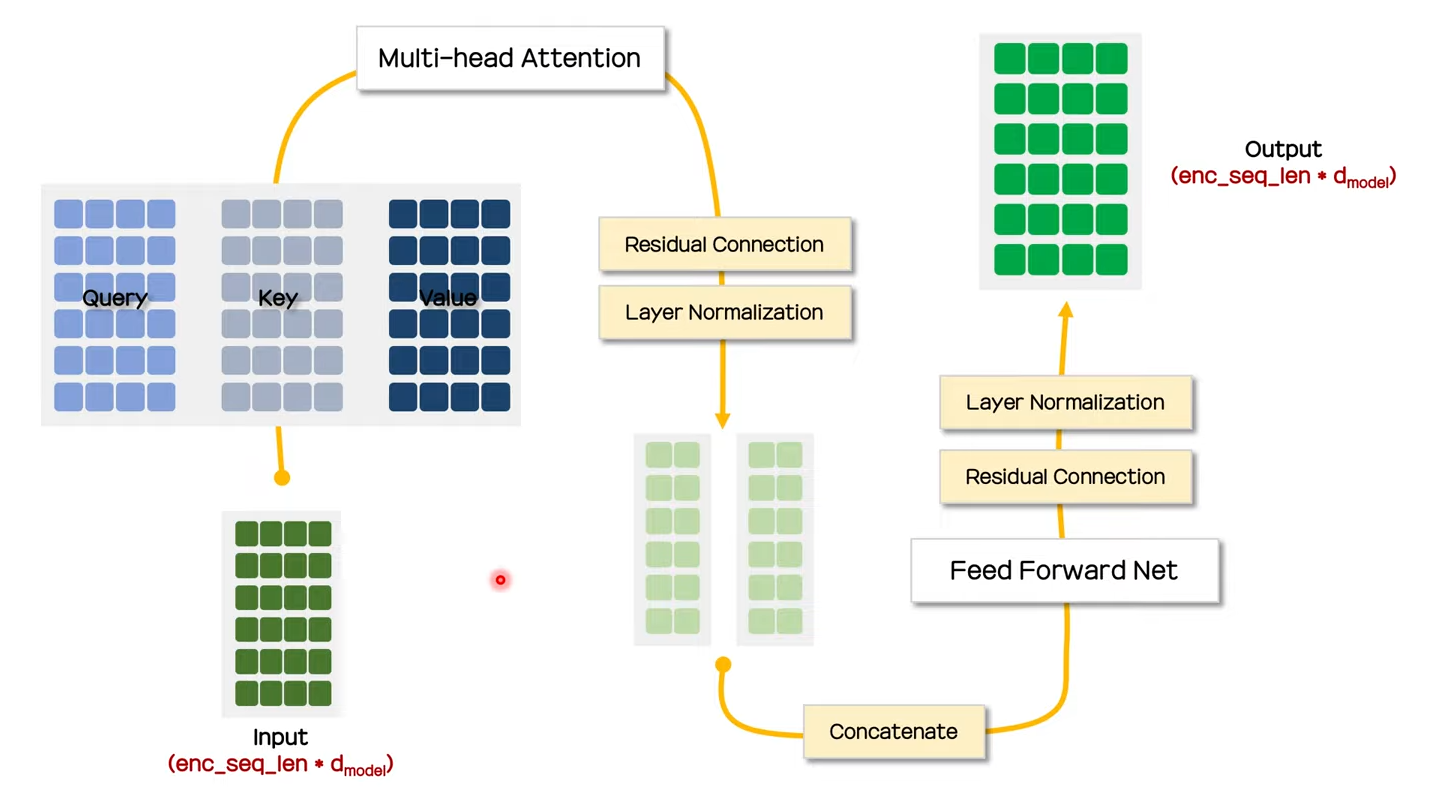
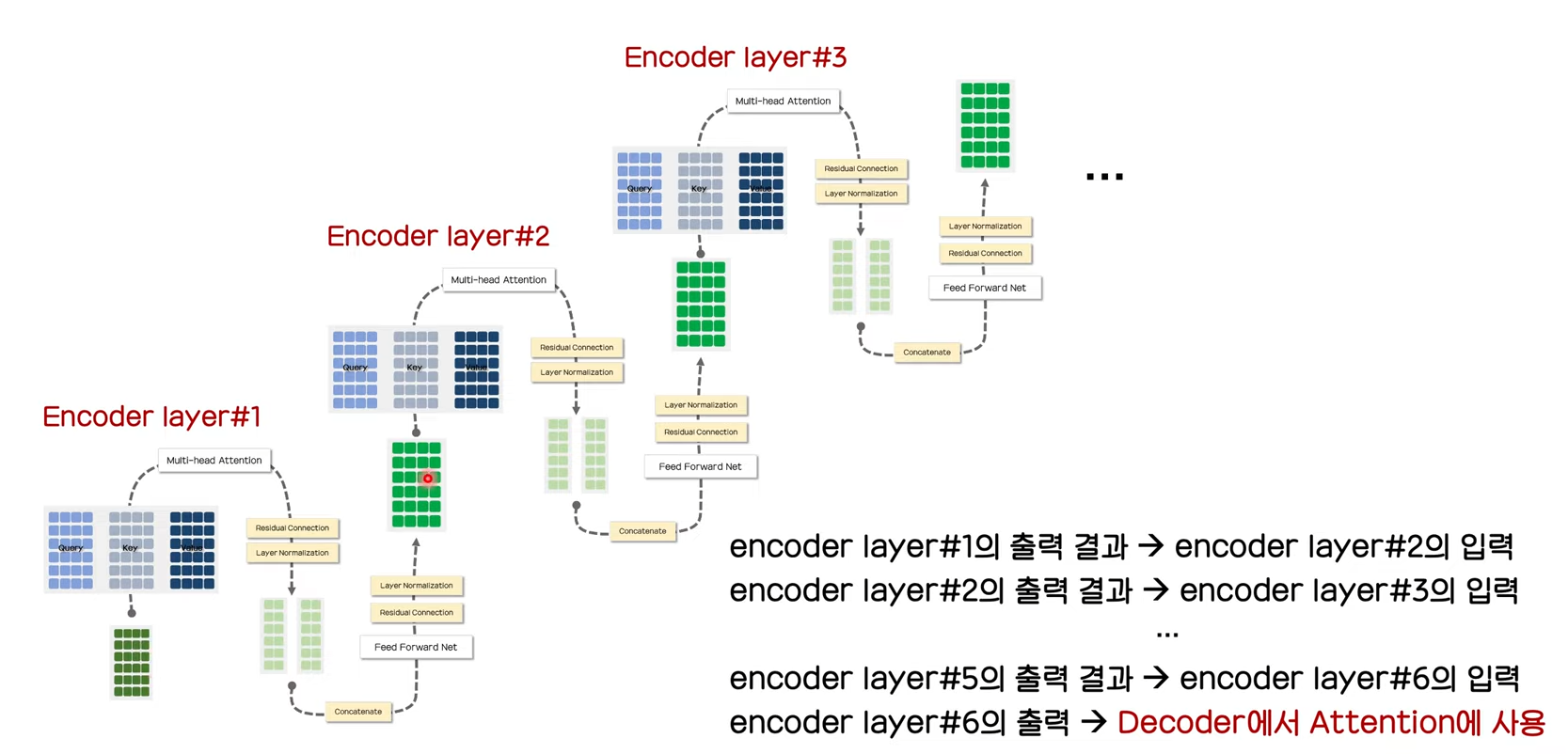
Encoder의 구조에 대해서 알아보았고 마지막으로 전체적인 구조를 살펴보고 우선 마무리 하도록 하자.
'Robotics & AI > Paper review' 카테고리의 다른 글
| BERT(1) (0) | 2023.08.02 |
|---|---|
| [논문 리뷰] Attention is all you need (2) (0) | 2023.07.25 |
| [논문 리뷰] AutoRec: Autoencoders Meet Collaborative Filtering (0) | 2023.07.10 |
| [논문 리뷰] Long Short-Term Memory (0) | 2023.03.12 |
| [논문 리뷰] Deep Sparse Rectifier Neural Networks (2) | 2023.02.05 |



