Regularization

위와 같은 경우에 weight W는 유일하게 결정될 수 없다.

Hinge loss의 특징을 통해서 2W 또한 Loss를 0으로 만들 것이라고 예상할 수 있다.

이 케이스에서 weight를 두배로 만들어도 아래와 같이 Loss는 계속 0임을 확인할 수 있다.

Regularization의 기본 원리는 이왕이면 더 단순한 모델이 좋다는 것이다. 아래 케이스를 보면 f1이 f2보다 training set에 보다 적합하지만 너무 복잡한 것을 볼 수 있다. 이렇게 과적합이 되어있으면 다른 데이터가 들어왔을때 좋은 성능을 내기 어렵다.

다른 데이터가 들어오자 더 단순한 f2가 더 잘 표현하고 있는 것을 볼 수 있다.

많이 알려진 regularization 기법은 아래와 같다.

L1 regularization은 Lasso라고도 불리고 L2 regularization은 ridge라고도 불린다. 또한 둘을 합친 기법이 Elastic net이다.
추가로 Dropout, Batch normalization등이 있다.

Dropout은 너무나 흔하고 쉽고 간단한 기법으로 매 training cycle마다 random한 뉴런이 학습되지 못하도록 drop하여 다양한 뉴런 조합으로 학습을 하여 한두개의 뉴런에 과하게 의존하는 현상을 방지하는 기법이다.

Batch normalization은 학습 과정에서 각 배치 단위 별로 데이터가 다양한 분포를 가지더라도 각 배치별로 평균과 분산을 이용해 정규화하는 것을 뜻한다. 위 그림을 보면 batch 단위나 layer에 따라서 입력 값의 분포가 모두 다르지만 정규화를 통하여 분포를 zero mean gaussian 형태로 만든다.
Dimensional Reduction/Expansion
Curse of Dimensionality(차원의 저주)는 원래는 가까운 값이 차원이 증가하며 점점 멀어지는 것이다.

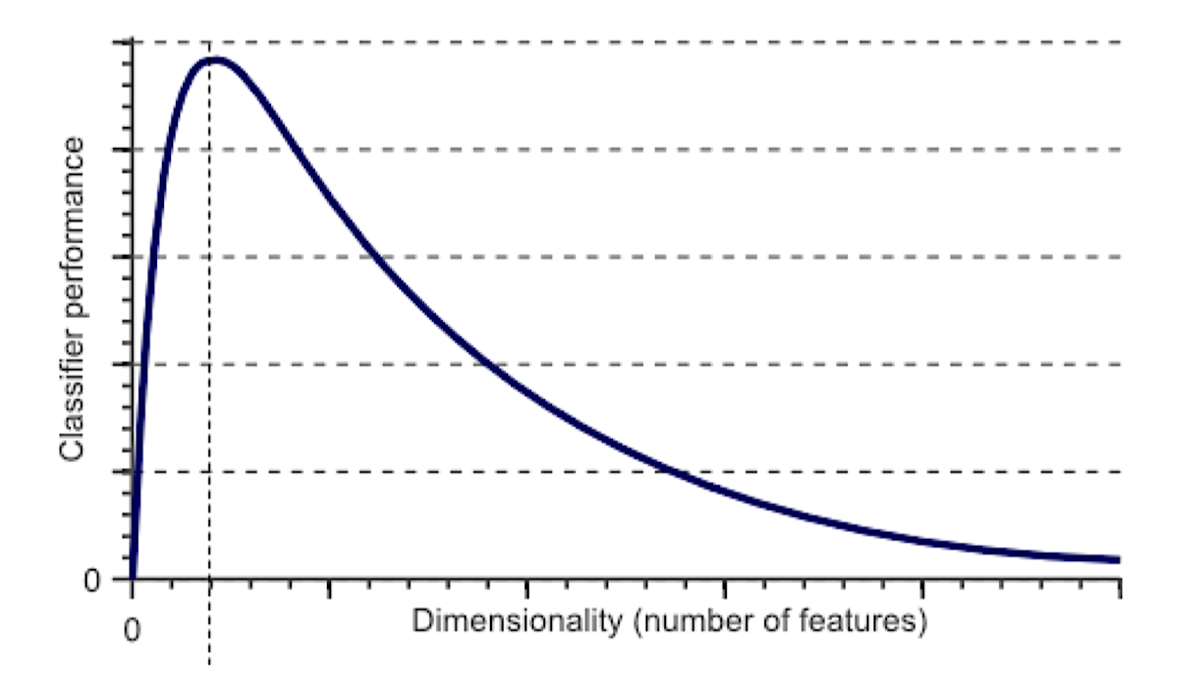
차원이 너무 높아지면 성능이 낮아지는 것을 볼 수 있다.
이러한 문제를 방지하기 위한 다양한 차원 축소 기법이 존재한다.

PCA (Principal Component Analysis, 주성분 분석)는 데이터의 분산을 최대화하는 성분 축을 찾아 고차원 데이터를 저차원으로 투영한다. 이는 데이터의 주요 패턴을 발견하는 데 유용한 기법이다.
LDA (Linear Discriminant Analysis, 선형 판별 분석)는 클래스 간 분리를 최대화하는 방향을 찾아, 분류 문제에서 유용하게 사용된다. 즉, 다른 클래스의 데이터를 가장 잘 구분할 수 있는 축을 찾는 기법이다.
t-SNE (t-Distributed Stochastic Neighbor Embedding): 고차원 데이터의 유사한 확률 분포를 저차원에서도 유지하려고 시도하는 기법으로, 특히 고차원 데이터의 구조를 시각화하는 데 유용하다.
반대로 아래는 차원을 확장하는 Dimension Expansion과정이다.
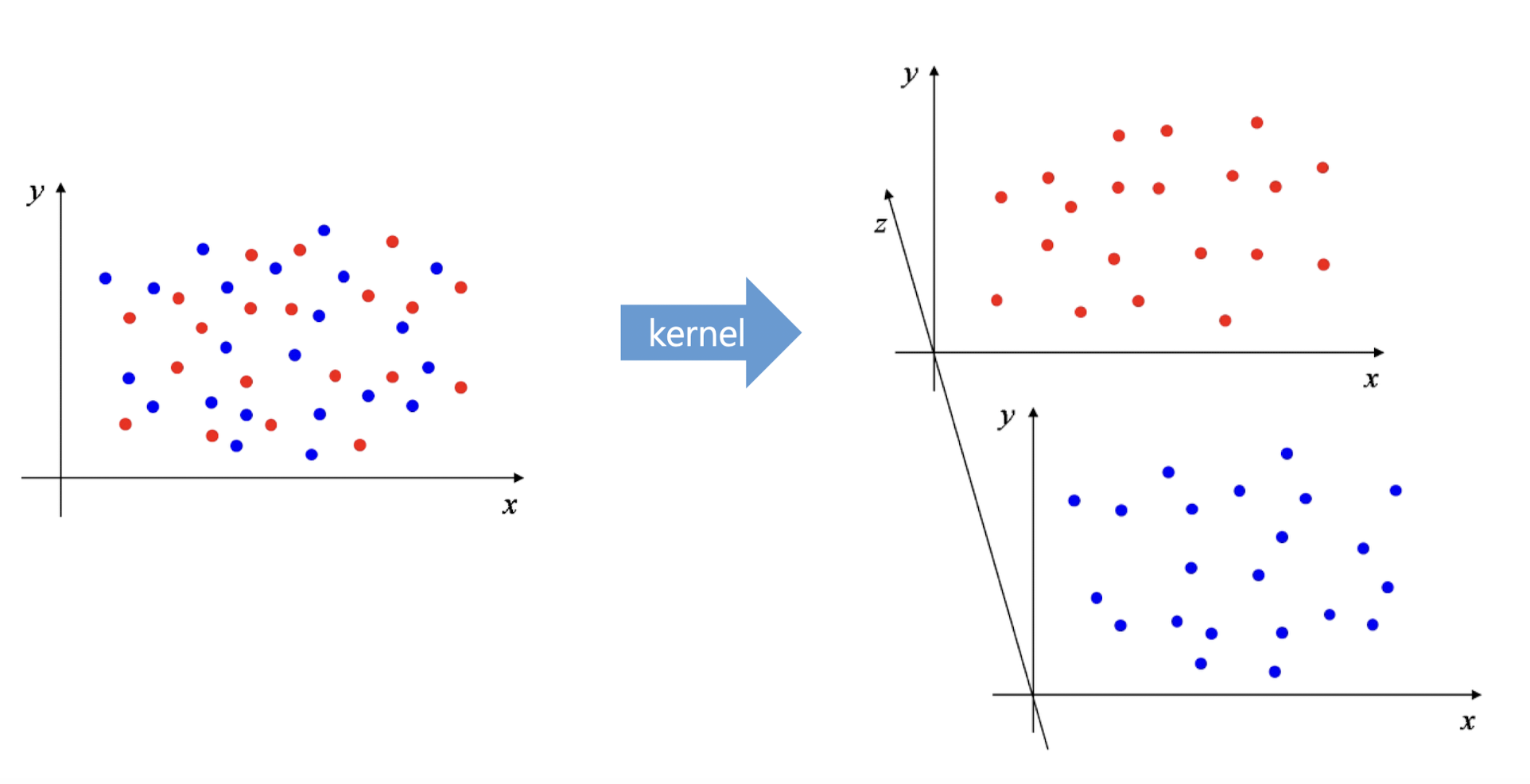
이러한 기법은 다음과 같은 상황에서 유용하게 사용된다.
비선형 관계 모델링: 데이터 간 복잡한 비선형 관계가 있을 때, 차원 확장을 통해 데이터를 고차원 공간으로 매핑하면 선형 모델을 사용하여 비선형 문제를 해결할 수 있다. 예를 들어, 서포트 벡터 머신(SVM)에서 커널 트릭은 입력 데이터를 고차원 특징 공간으로 매핑하여 더 쉽게 분리 가능하게 만든다.
특징 향상: 기존의 특징이 모델의 성능을 제한할 때 추가적인 특징을 생성하거나 기존 데이터의 변형을 통해 더 많은 정보를 추출할 수 있다. 예를 들어, 이미지 처리에서는 원본 픽셀 데이터에 여러 필터를 적용하여 새로운 특징을 생성하기도 한다.
딥 러닝: 신경망에서는 종종 입력 데이터를 여러 층을 거쳐 점차적으로 고차원 특징으로 변환한다. 이 과정에서 더 복잡한 패턴이나 추상적인 특징이 학습될 수 있다.
다양한 데이터 통합: 서로 다른 종류의 데이터 소스를 통합할 때, 각 데이터 소스를 동일한 차원의 특징 공간으로 확장하여 일관된 분석이 가능하게 할 수 있다.
기본적으로 모델을 데이터에 적합하게 복잡화를 하다보면 발생하는 것이 차원 증폭이라고 보면 된다.
'Quality control (Univ. Study) > AI Applications' 카테고리의 다른 글
| Computational Graph / Backpropagation (0) | 2024.05.03 |
|---|---|
| 시험 대비 코드 정리(2) (0) | 2024.04.22 |
| 시험 대비 코드 정리(1) (0) | 2024.04.19 |
| Optimizer (0) | 2024.04.17 |
| Softmax classifier (0) | 2024.03.31 |

