Gradient


위와 같은 SVM Loss function에 대해서 어떤 식으로 gradient를 연산할지 생각해보자.
당연히 직접 계산을 하나씩 해나갈 수 있다.

그러나 당연하게도 직접 하나하나 계산하는 것은 어마어마한 양의 행렬 연산으로 인해 낭비가 많다. 또한 만약 Loss function을 바꾸고 싶어지면 연산을 처음부터 다시해야한다. 마지막으로 복잡한 모델에서는 더더욱 문제가 많을 것이다.
따라서 Computational graphs와 Backpropagation을 이용한다. 아래는 Computational graphs의 표현법이다.

역전파의 간단한 예시를 살펴보자.

우리가 알고있는 미분 값과 알고 싶은 미분 값은 아래와 같다.

이를 chain rule을 이용하여 역으로 진행시켜 구할 수 있다.


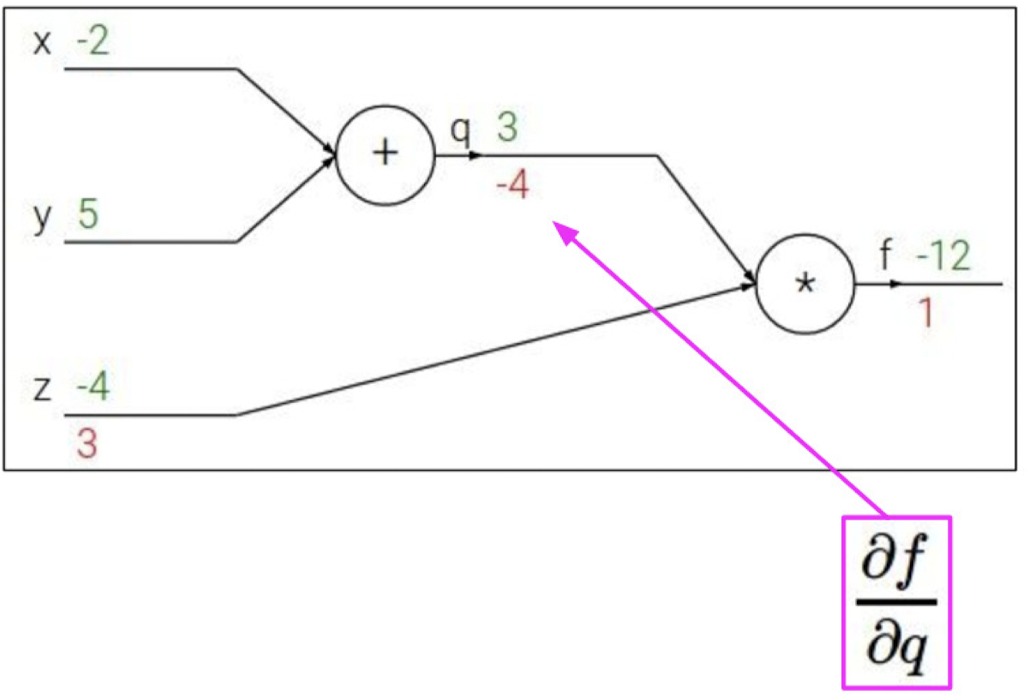
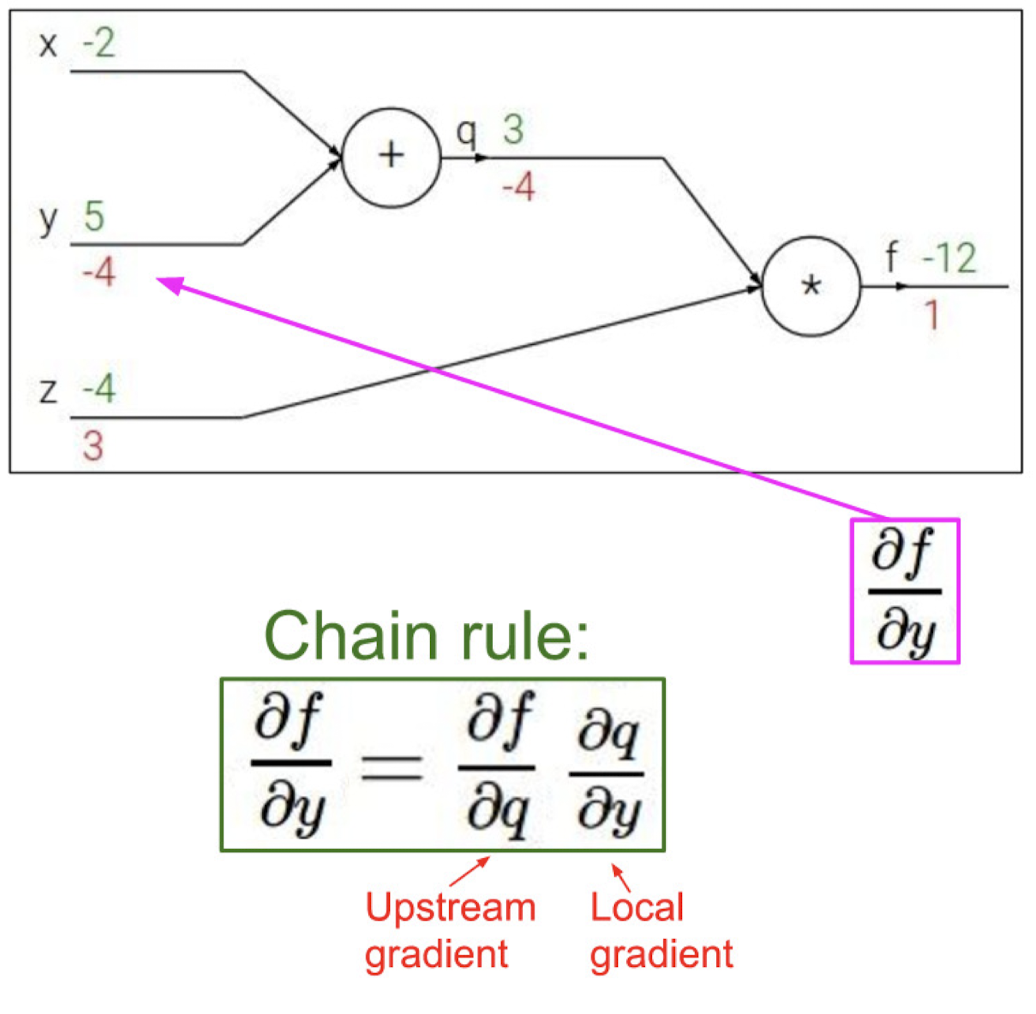
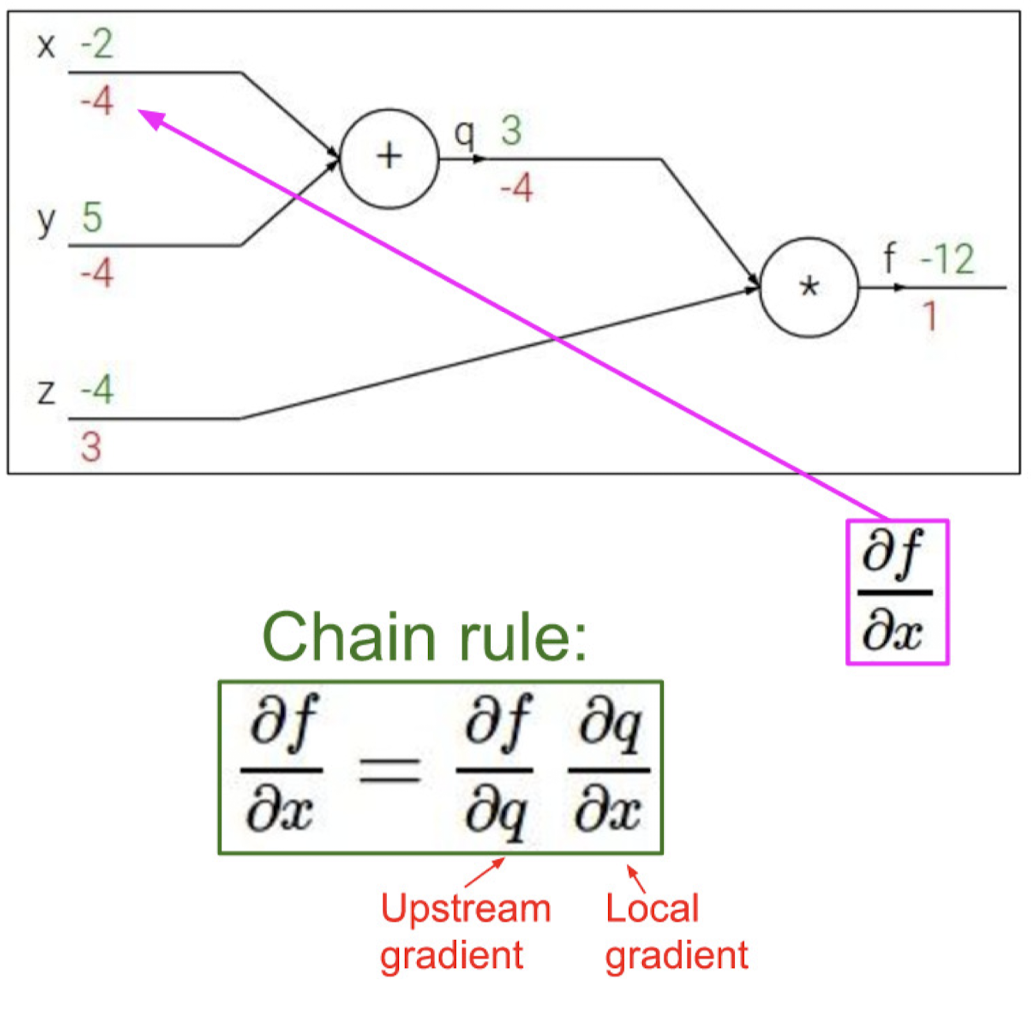
위 과정을 다시 한번 살펴보면 아래와 같다.
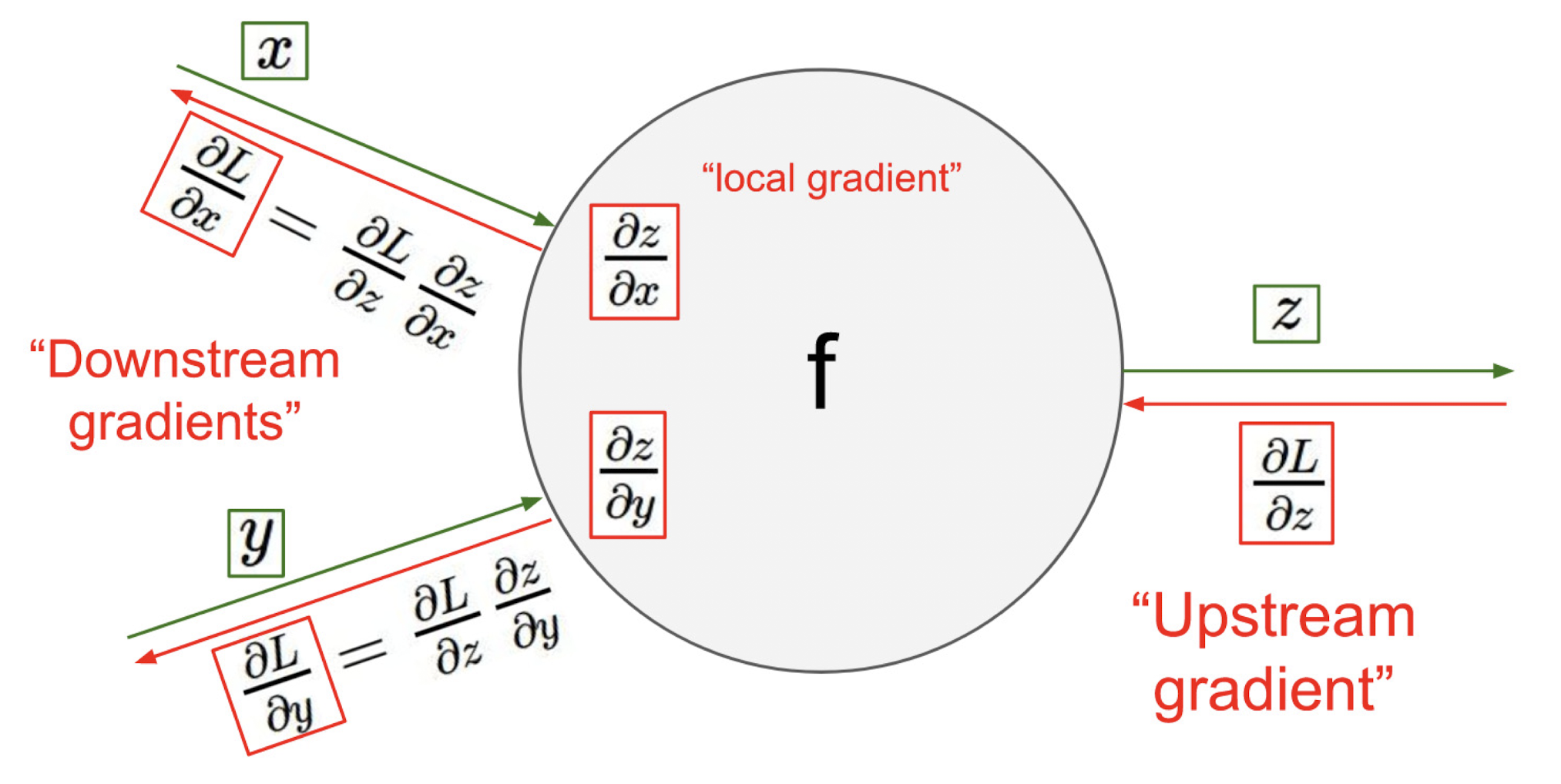
Loss를 미분해서 찾은 Upstream gradient와 이후에 추가로 계산한 local gradient를 chain rule로 계산을해 Downstream gradients를 찾는 것이다.
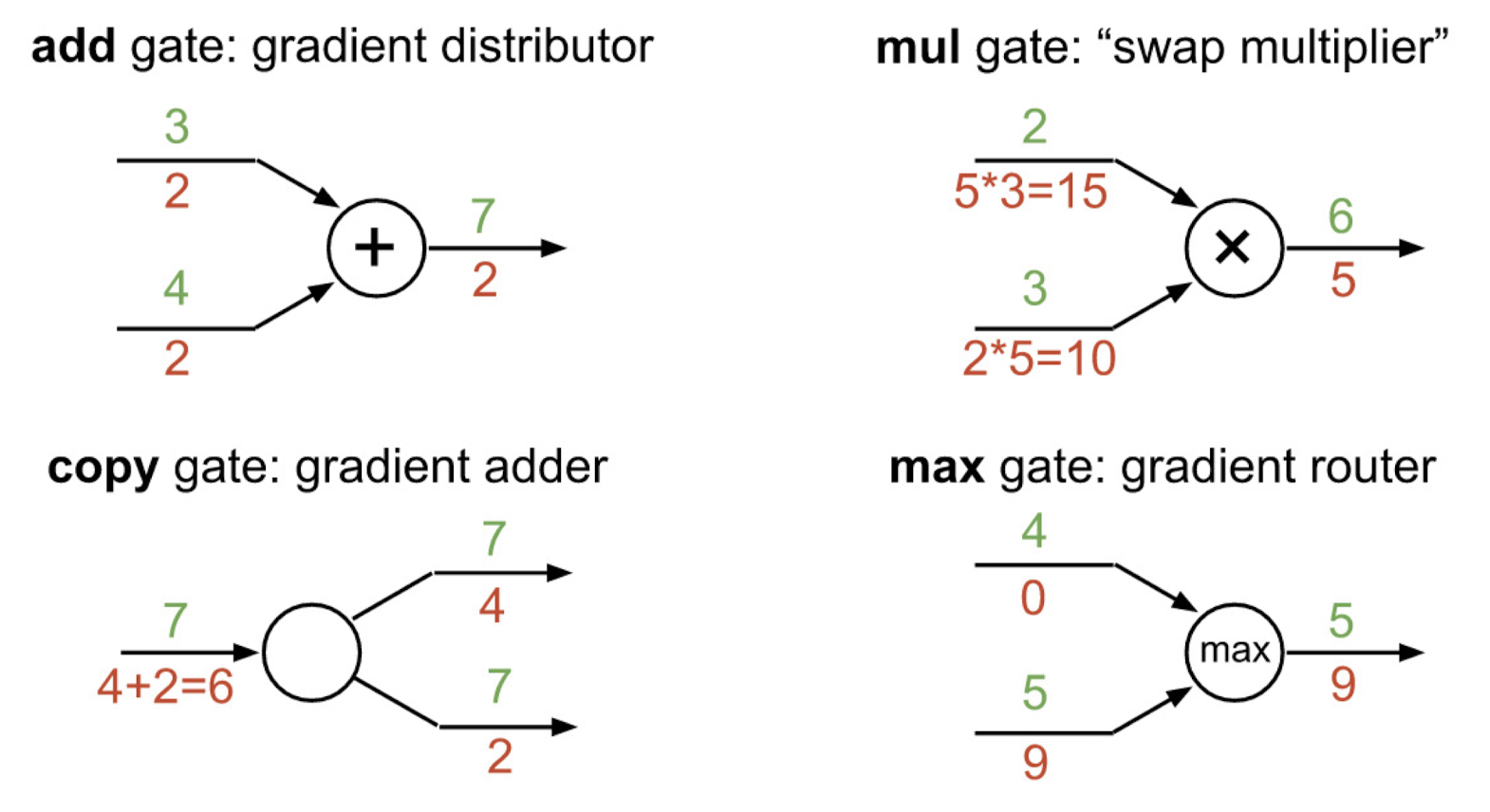
위와 같은 연산법으로 gradient pattern을 연산하면 된다. 마지막으로 sigmoid function을 이용한 case를 통해 다시 한번 backpropagation 전파 과정을 살펴보자.
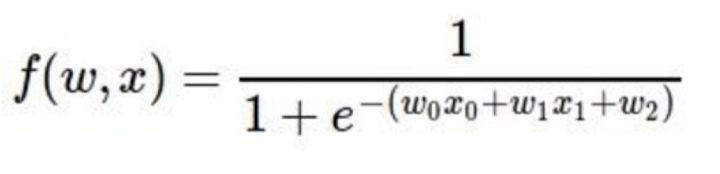
위와 같은 식을 graph로 나타내고 local gradient를 계산한 결과이다.
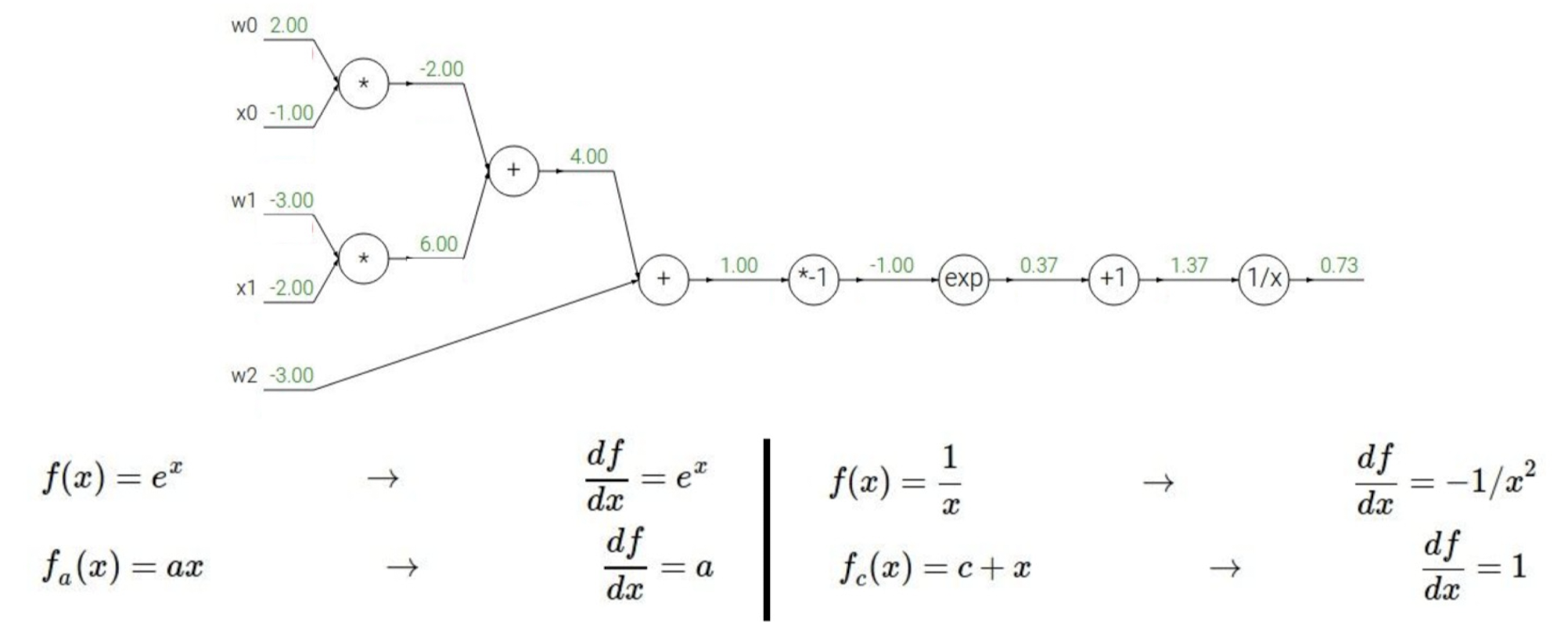
과정을 하나씩 따라가보자.
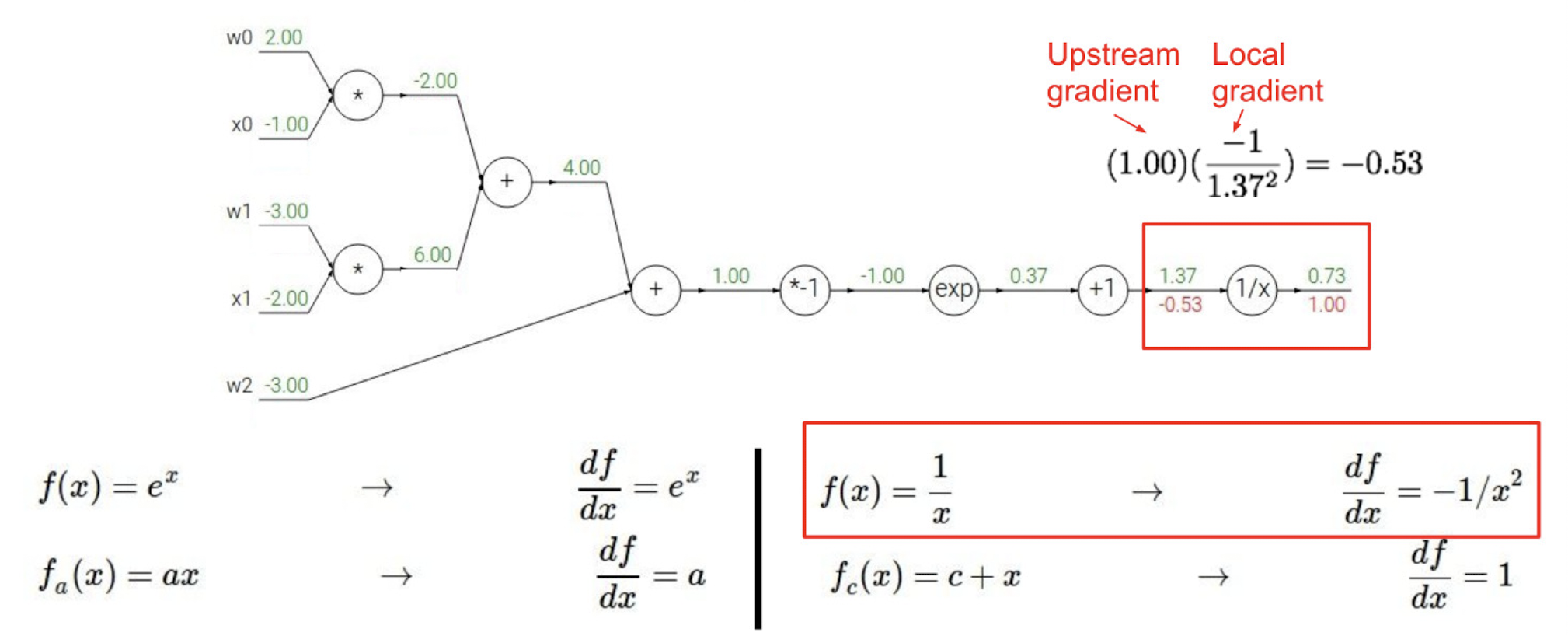
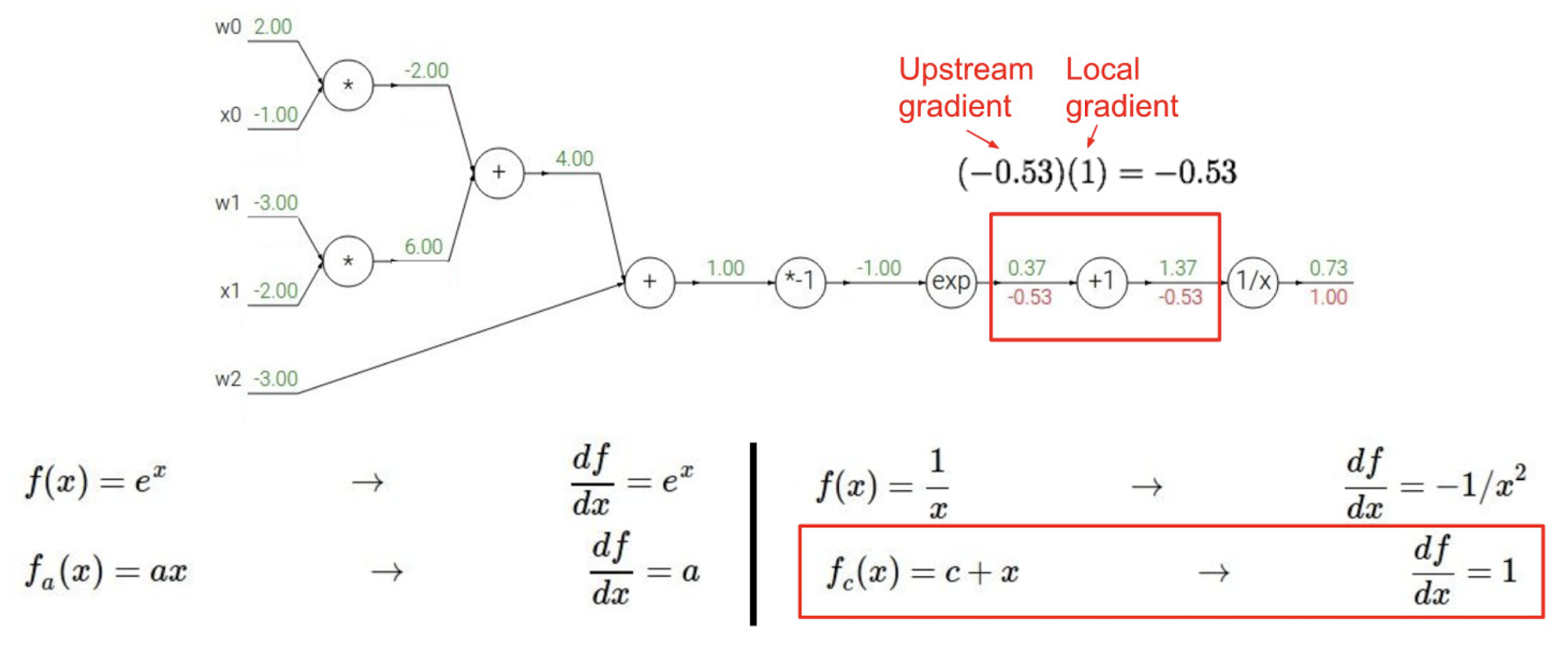
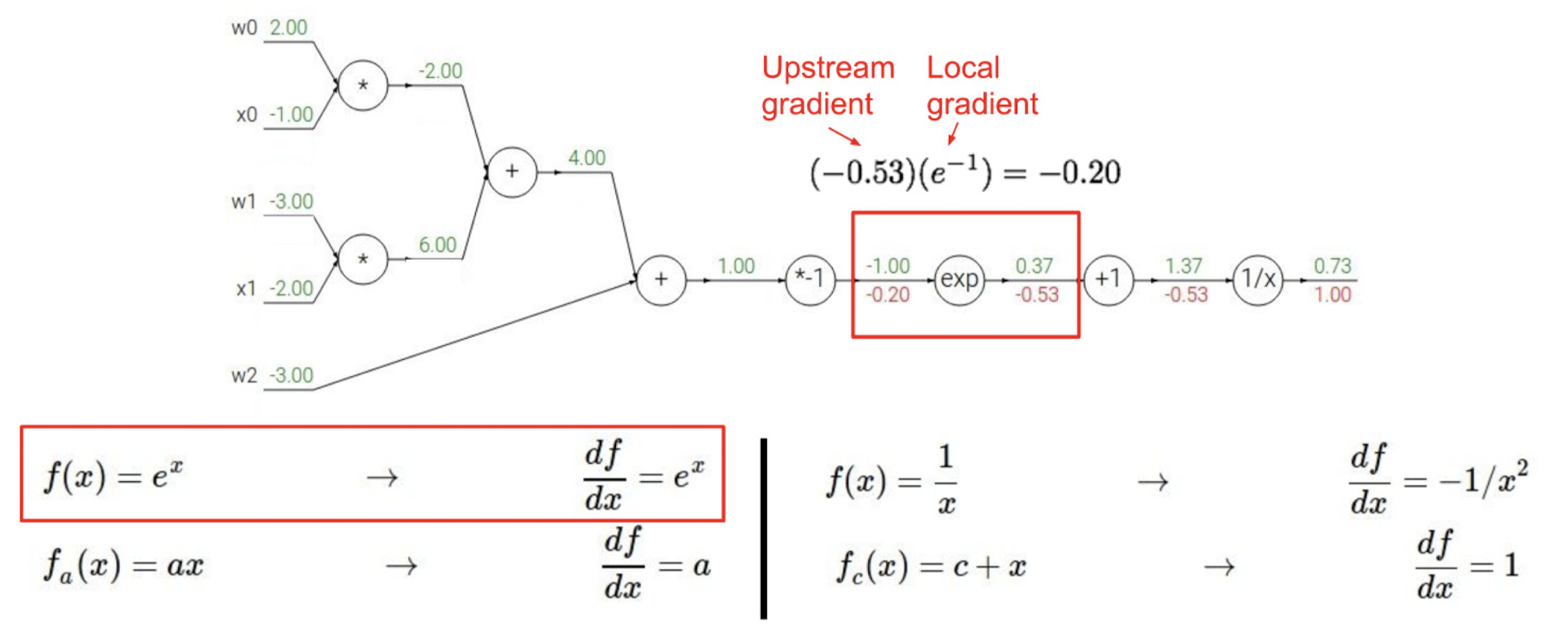
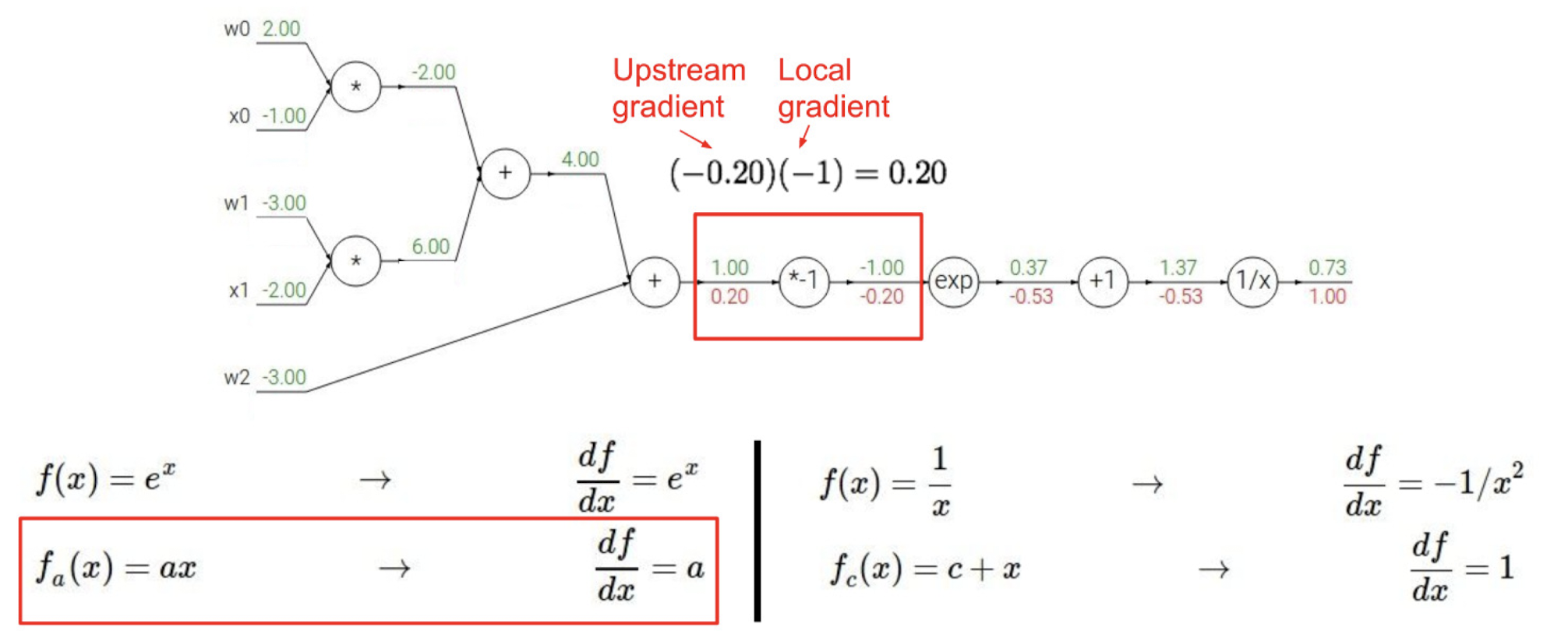
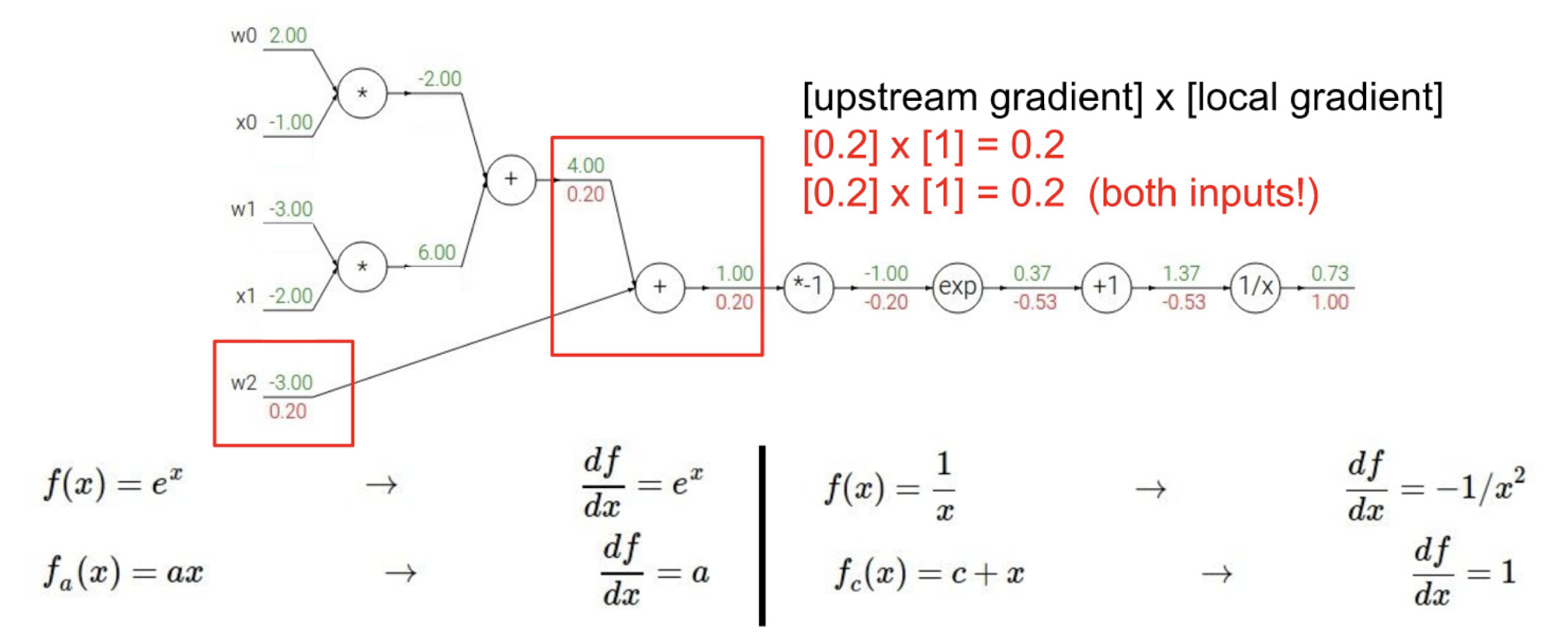
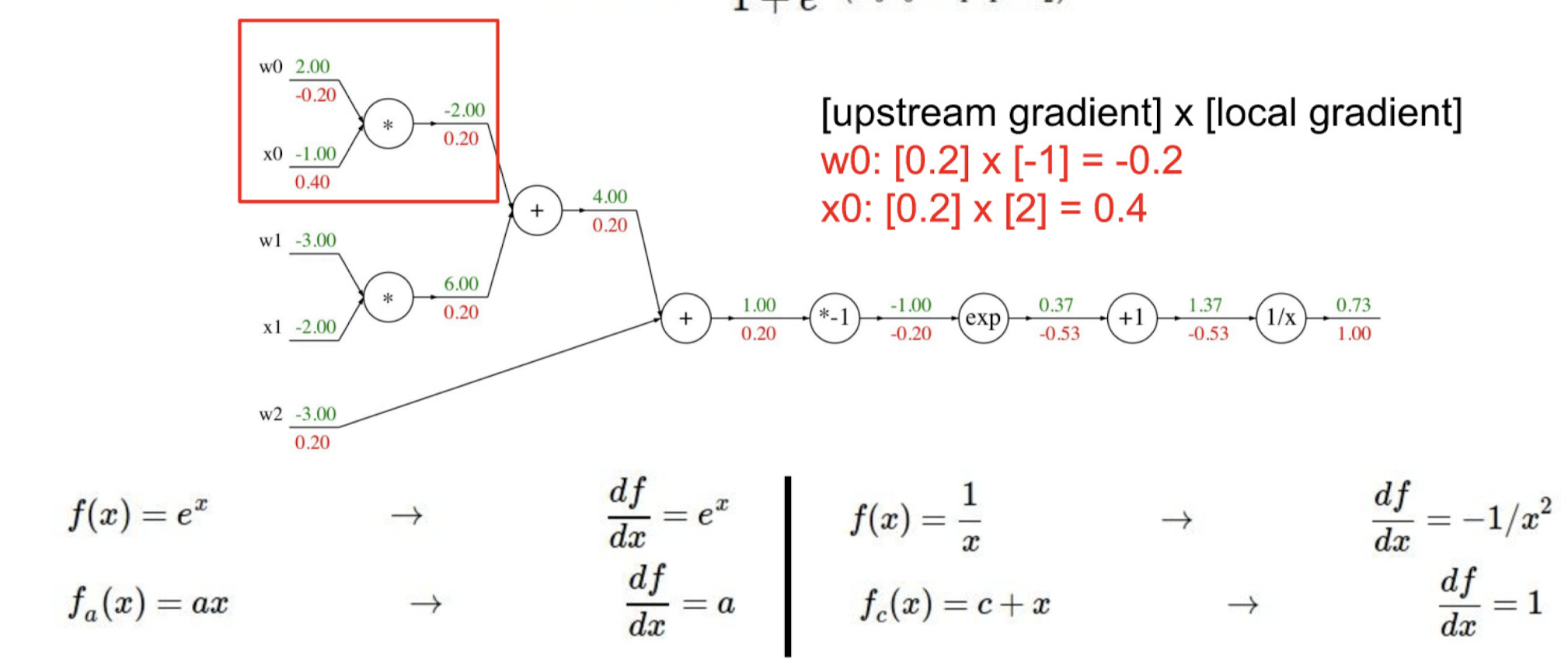
sigmoid 함수에서 역전파 과정만 다시 살펴보자면 아래와 같은 방식으로도 표현할 수 있겠다.

'Univ. Study > AI Applications' 카테고리의 다른 글
| Regularization / Dimensional Reduction and Expansion (0) | 2024.05.04 |
|---|---|
| 시험 대비 코드 정리(2) (0) | 2024.04.22 |
| 시험 대비 코드 정리(1) (0) | 2024.04.19 |
| Optimizer (1) | 2024.04.17 |
| Softmax classifier (0) | 2024.03.31 |

