File compression
시간보다는 공간을 절약하는 방법에 대해 연구된다. 대부분의 컴퓨터 화일에서 데이터가 중복되어 있다는 것에 착안된 개념이다. 파일 압축의 대상으로는 텍스트 파일 인코딩된 이미지의 래스터 파일 사운드나 다른 아날로그 신호의 디지털 표현 등이 있다. 현재는 허프만 인코딩이 거의 주를 이루지만 이 개념이 나오기까지 몇몇 다른 시도들이 존재했었다. 우선 run-length encoding(런-길이 인코딩)은 동일한 문자가 여러개 나올 경우 숫자와 문자쌍으로 화일을 압축하는 기법이다. 이진수로 표현되는 비트맵 이미지를 압축하는데 사용됐었다. 화일에서 가장 기본적인 중복은 같은 문자가 연속적으로 나타나는 것이다. 이를 다음과 같이 압축해내는 기법이다.
AAAABBCCC → 4A2B3C
0000001111000 → 6 4 3
그러나 문자를 사용한 화일 압축 기법은 숫자와 문자가 혼합되어 있는 화일에는 적용할 수 없다. 따라서 텍스트에서 드물게 나타나는 문자를 탈출 문자(escape character)로 사용한다. 탈출 순차(escape sequence) : 탈출 문자, 개수, 1개의 반복 문자
- AAAABBCCCCC → QDABBQEC
- Q : Q<space>
- 50개의 B : QZBQXB
이를 개선한 방법이 가변-길이 인코딩(variable-length encoding)으로 자주 나타나는 문자에는 적은 비트를 사용하고 드물게 나타나는 문자에는 많은 비트를 사용하여 인코드(encode)하는 압축 기법이다.
기존에는 ABRACADABRA 에 다섯 비트를 사용하면 아래와 같이 인코딩이 되었다.

0000100010100100000100011000010010000001000101001000001
엄청나게 길어진 것을 볼 수 있다. 그러나 가변 길이 인코딩 기법을 이용하면 아래와 같이 인코딩이 될 수 있다.
0 1 01 0 10 0 11 0 1 01 0
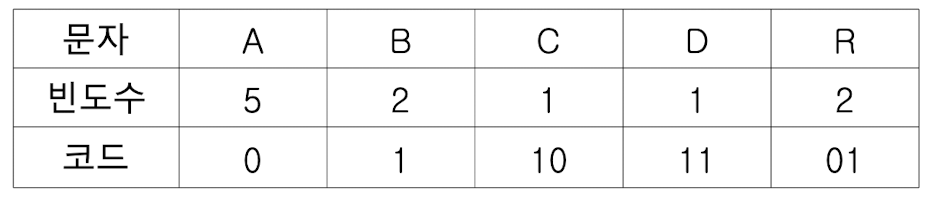
그러나 C가 B의 코드인 1을 접두사로 사용하여 C와 BA를 구분할 수 없게되는 문제가 있다. 이를 해결하기 위해 하나의 문자코드가 다른 문자코드의 접두부가 되지 않는 것을 보장하는 자료구조인 Trie(트라이)가 사용된다. 트라이는 비트스트링을 유일하게 디코드 할 수 있고 하나의 문자열로부터 여러 개의 트라이를 생성할 수 있다.
따라서 여러개의 트라이중에서 어떤 것이 가장 효율적인 것인지를 결정하는 방법이 있어야한다. 이러한 것을 모두 고려하여 개발된 기법이 허프만 인코딩이다.
Huffman Encoding
허프만 인코딩은 여러 트라이중 가장 좋은 트라이를 결정하는 일반적인 기법이다. 우선순위 큐(Priority Queue)를 사용하여 빈도수가 가장 작은 문자부터 차례로 트라이를 만든다. 인코딩된 메시지의 길이는 허프만 빈도수 트리의 가중치 외부경로의 길이(weighted external path length)와 같게 된다. 동일한 빈도수를 가지는 경우에는 허프만 트리가 최적해가 된다.
struct nodetype
{
char symbol;
int frequency;
nodetype* left;
nodetype* right;
}
//“데이터+빈도수” 노드를 모두 PQ에 insert
for(i=1; i<=n; i++)
{
remove(PQ, p);
remove(PQ, q);
r = new nodetype;
r->left = p;
r->right = q;
r->frequency = p->frequency + q->frequency;
insert(PQ, r);
}
remove(PQ, r);
return r;작동과정을 같이 살펴보자. 우선 주어진 텍스트의 빈도수를 계산한다.

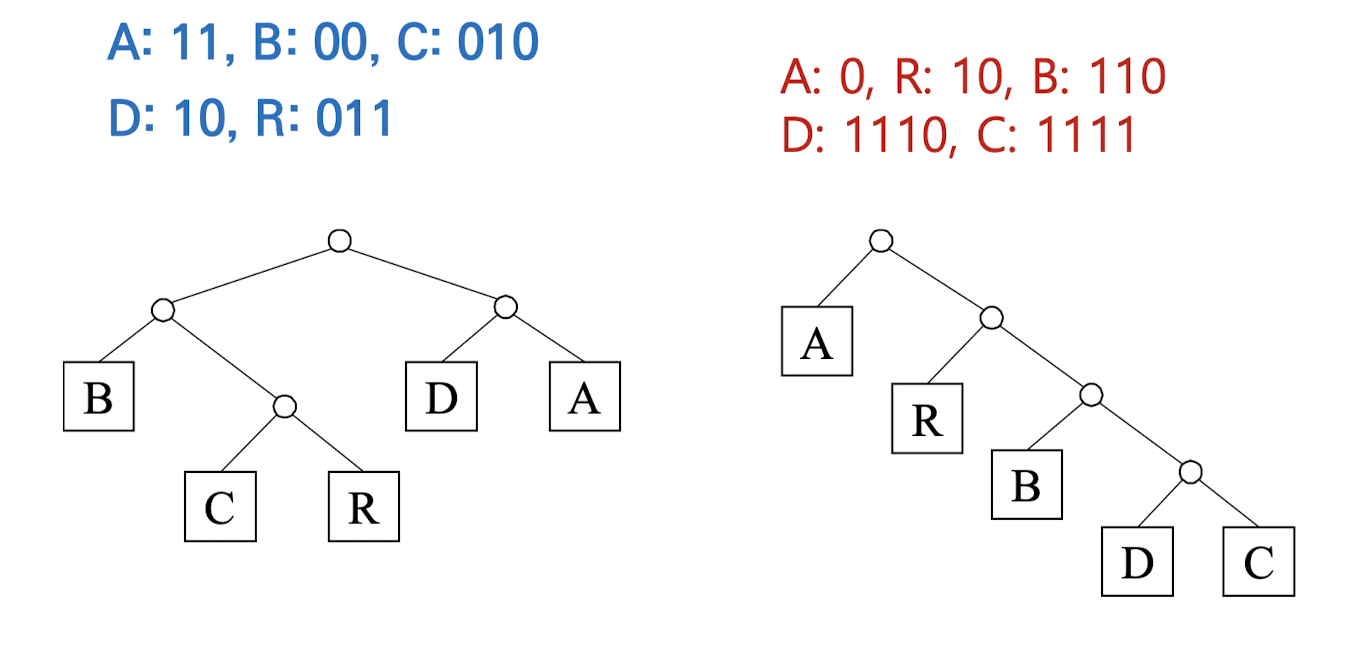
이제 허프만 트리를 빈도수가 적은 순서대로 구성해나간다.



결과적으로 아래와 같이 빈도수가 많은 문자들이 가장 짧은 비트로 인코딩이 되었고 어떠한 변환값도 다른 값의 접두부가 되지 않는다.

데이터 암호화
암호화 시스템은 암호화 알고리즘(E), 해독 알고리즘(D) 암호화키(K)로 구성되어 있다. 또한 흔히 전송이나 저장해야 될 원시 데이타인 평문을 P, 암호화된 암호문을 C로 표현한다.
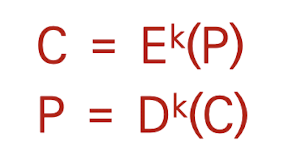
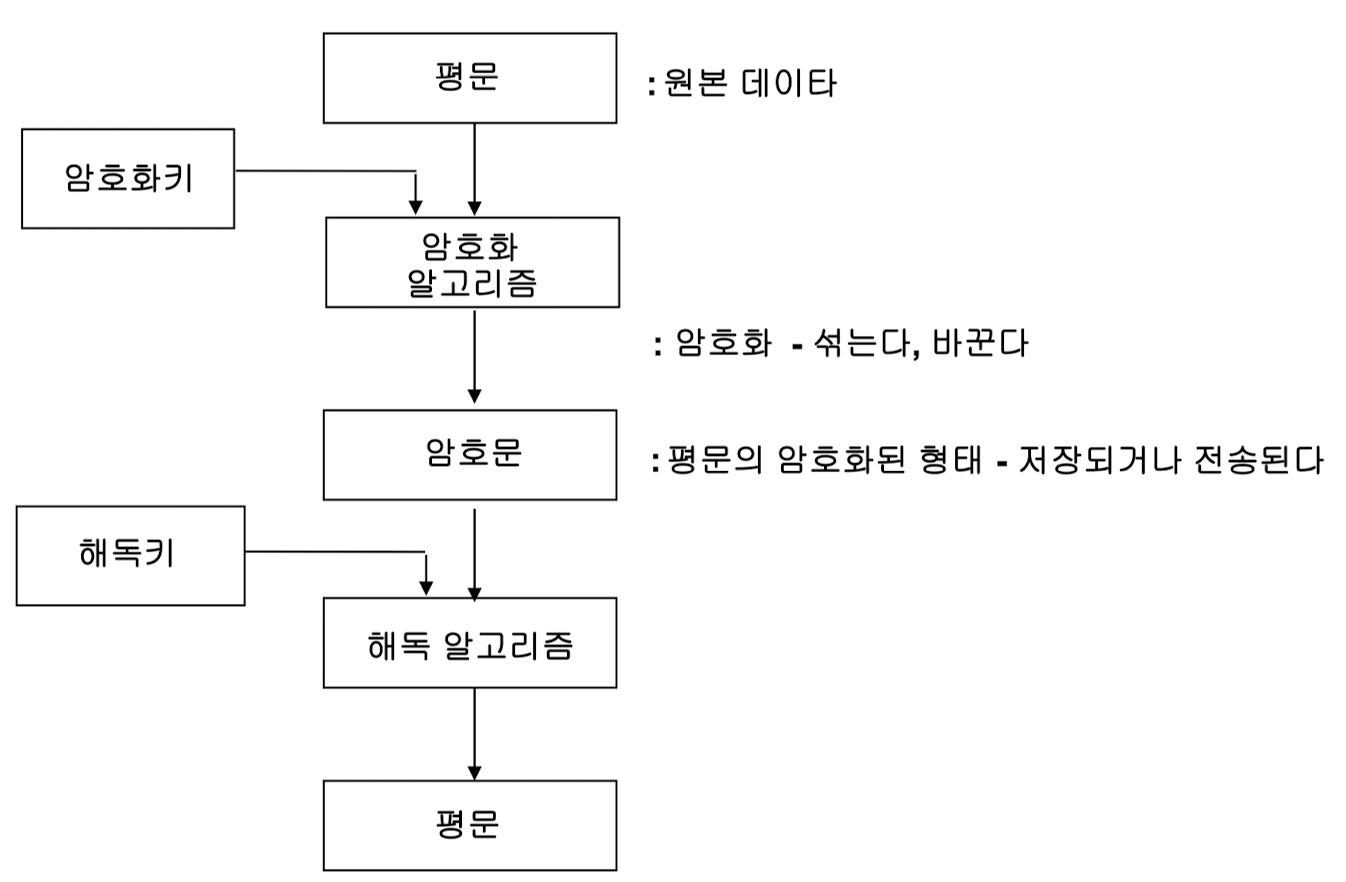
위와 같은 과정을 통해 암호화, 복호화 과정이 일어나는 것이다. 대칭키를 이용하는 경우는 암호화키와 해독키가 일치하는 것이고 비대칭키를 이용하는 기법은 암호화키는 공개키로 사용하되 해독키를 공개하지 않는 방식을 이용한다.
암호화 기법은 크게 두가지가 존재한다. 우선 전치 기법(transposed method)은 데이타의 문자들을 순열로 만드는 것이다. 간단한 예를 살펴보면 데이터를 두 문자씩 나누고 두 문자를 서로 교환하는 규칙을 가진 암호화기법이 있을 수 있다.
평문이 DATABASE MANAGEMENT일때 암호문은 ADATABESM ♭ NAGAMENE ♭ T이 될 것이다. 다음으로 대체 기법(substitution method)은 평문의 문자 정보를 다른 문자 정보로 대체하는 것이다. 그 과정의 예시 하나를 자세히 살펴보자.
평문 : THE PRESIDENT LEFT
암호화키 : SECRET (length: 6)
위와 같이 조건이 주어졌을 때의 경우이다.
1단계 : 평문을 암호화키와 같은 길이의 블록으로 나눈다.
THE♭PR ESIDEN T♭LEFT
2단계 : 대체할 문자 코드를 ♭=00, A=01, B=02, ... , Z=26 으로 정하고 해당 정수 코드로 대체한다.
200805001618 051909040514 200012050620
3단계 : 암호화키에 대해서 2단계 적용한다.
SECRET
190503180520
4단계 : 문자별로 (블록+암호화키) mod 27을 연산한다. (character by character)
200805001618 051909040514 200012050620
+)190503180520 +)190503180520 +)190503180520
----------------- ------------------ ------------------
121308182111 242412221007 120515231113
5단계 : 정수 코드에 해당하는 문자로 바꾸어 암호문을 얻는다.
암호문 : LMHRUK XXLVJG LEOWKM
해독과정은 (블록-암호화키) mod 27이 된다.
121308182111
-) 190503180520
------------------
200805001618 mod 27
THE♭PR
RSA
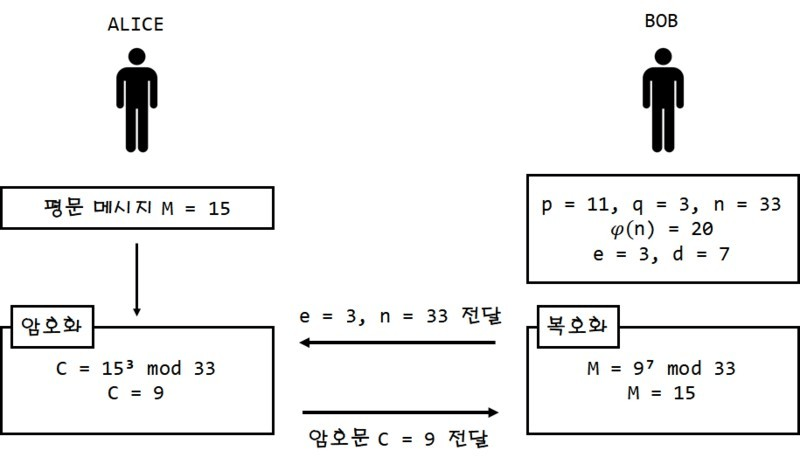
RSA알고리즘 은 Rivest, Shamir and Adleman이 개발하여 RSA라고 이름이 지어졌고 공개 키 암호화 시스템에서 사용되는 대표적인 알고리즘이다. 공개키 암호화 시스템에서 암호화키와 알고리즘은 공개가 되어있고 해독키, 해독 알고리즘은 비밀이다. 해독키는 암호화키로부터 유도가 불가능하도록 설계되어있다. 안전하게 키를 분배하는 문제를 해결하기 위해 개발되었다. 메시지를 보낼 때 송신자는 수신자의 공개키를 찾아 사용하여 암호화한 후 전송하고 메시지를 읽을 때는 수신자가 자신이 가진 비밀 키(secret key)를 사용하여 복호화한다. 서로다른 키로 같은 결과를 얻어낼 수 있다는 것이 해당 시스템의 놀라운 점이다.
P를 공개 키, S를 비밀 키, M을 메시지라고 할때 조건은 다음과 같다.
1. S(P(M)) = M
2. 모든 (S, P) 쌍은 유일해야 한다.
3. P로부터 S를 알아내는 것은 M을 해독하는 것만큼 어려워야 한다.
4. S와 P는 쉽게 계산할 수 있어야 한다.
RSA 알고리즘은 메르센이 제시한 전제인 "주어진 큰 숫자가 소수인지를 결정하는 빠른 알고리즘은 있지만, 주어진 큰 비소수의 소수 인자를 찾아내는 빠른 알고리즘은 없음"을 이용한다. 예를 들어 130자리 수가 소수인지 검사하는 데는 7분밖에 걸리지 않지만 두개의 63자리 소수를 곱하면 비소수가되는데 이 비소수의 소인수를 찾아내는 데는 4 X 10^16년이 소요한다.
또한 RSA는 그 단순성으로 메시지를 선형 시간에 암호화할 수 있다.
수행 절차는 다음과 같다.
1. 서로 다른 두개의 큰 (100자리)소수 p, q를 선택한다.
r←p*q
2. 하나의 큰 숫자 e(암호화 키)를 (p-1)*(q-1) 에 대한 상대적 소수 , p ,q보다 큰 어떤 소수로 설정한다.
3.해독키 d를 e modulo (p-1)*(q-1) 의 유일한 곱셈 역이 되는 것으로 만든다. d*e = 1 modulo (p-1)*(q-1)
4. 정수 r과 e는 공개하고 d는 비밀로 유지한다.
5. 평문 P로부터 암호문 C= P^e modulo r를 계산하여 암호화를 한다.
6. 암호문 C로부터 평문 P= C^d modulo r를 계산하여 복호화를 한다.
예시를 통해 살펴보자.
1. p=3,q=5 →r=15
2. (p-1)*(q-1) = 2*4 = 8
let e be 11 (prime greater than both p, q) find d
3. d*11=1modulo8 → d=3
4. pass
5. let P =13(plain text)
C = P^e modulo r
= 13^11 modulo 15
= 1,792,160,394,037 modulo 15
= 7
6. C=7
P = C^d modulo r
= 7^3 modulo 15
= 343 modulo 15
= 13
e와 d는 서로 역이고 ( D(E(P)) = E(D(P)) = P )
r 과 e (not p or q)로부터 d를 계산하는 것은 불가능하다.
이는 소수기반 암호화 기법이고 일방 함수(oneway function)인 암호화 함수의 특성은 다음과 같다.
1. 모든 양의 정수 x에 대해 존재하는 E(x)는 유일하고 양수이다.
2. 모든 양의 정수 x에 대해 D(E(x))=x가 되는 역함수 D가 존재한다.
3. 주어진 x에 대해 E(x)와 D(x)를 계산하는 효율적인 알고리즘이 있다.
4. 함수 E로부터 D를 유도해 내는 것은 계산상으로 불가능하다.
'Quality control (Univ. Study) > Algorithm Design' 카테고리의 다른 글
| Algorithm design - Matrix-chain Multiplication (0) | 2024.05.07 |
|---|---|
| 알고리즘 설계 실습 - Fibo_counter (4) | 2024.05.01 |
| 알고리즘 설계 실습 - KMP (0) | 2024.04.17 |
| Algorithm Design - 라빈-카프 / 패턴 매칭 (0) | 2024.04.17 |
| Algorithm Design - 스트링 탐색 알고리즘(Naïve/KMP/BM) (0) | 2024.04.12 |


