스트링 탐색
문서에서 스트링을 탐색할 때 쓰이는 용어를 살펴보면 다음과 같다.
- 텍스트(text) : 문서
- 패턴(pattern) : 탐색할 스트링
- 스트링(string): 문자가 연속적으로 나열된 것, 텍스트(text) 스트링, 이진(binary) 스트링
스트링 탐색 알고리즘의 설계는 필연적으로 false start가 발생하는데 이 false start의 횟수와 길이를 줄여가는 것이다.
우선 가장 단순한 알고리즘부터 살펴보자.
Naïve Algorithm
Brute force 알고리즘이라고도 불리고 직선적 알고리즘이라고도 불리는 특별한 알고리즘이 없는(?) 알고리즘이다. 한 글자 또는 한 비트씩 오른쪽으로 진행하면서 텍스트의 처음부터 끝까지 모두 비교하며 탐색하는 방식을 이용한다.
BruteForce(p[], t[])
M ← 패턴의 길이; N ← 텍스트의 길이;
for (i ← 0, j ← 0; j < M and i < N; i ← i + 1, j ← j + 1) do
if (t[i] ≠ p[j]) then {
i ← i - j;
j ← -1;
}
if (j = M) then return i - M;
else return i;
end ButeForce()최악의 경우 시간 복잡도는 텍스트의 모든 위치에서 패턴을 비교해야 하므로 O(MN)이 된다.
표를 통해 어떻게 스트링을 비교하는지 살펴보면 아래와 같다.

KMP
KMP는 Knuth, Morris and Pratt의 준말로 세명의 대가가 만든 스트링 검색 알고리즘이다. 불일치가 발생했을 경우 텍스트 스트링의 앞 부분에 어떤 문자가 있는지를 미리 알고 있다면, 불일치가 발생한 앞 부분에 대해서는 다시 비교하지 않고 매칭을 수행하도록 하는 알고리즘이다. 패턴을 전처리하여 배열 next[M]을 구해두고 false start를 최소화하는 방식을 이용한다.
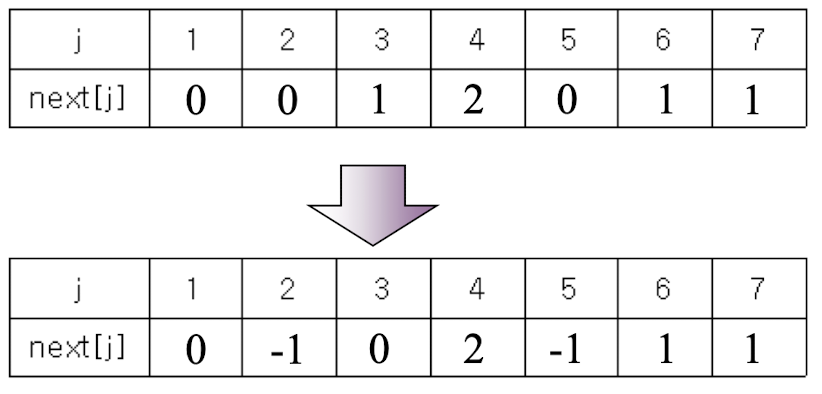
next[M]은 불일치가 발생했을 경우 이동할 다음 위치를 정해주는 값이다.
p[0~i]의 접미사와 일치한 최장 접두사의 끝자리에 위치하도록한다. (단, 최장접두사 != 전체문자열)
이때 시간 복잡도는 O(M+N)이 되어 Brute Force 알고리즘을 사용했을때 보다 훨씬 개선된것을 볼 수 있다.
InitNext(p[])
M ← 패턴의 길이;
next[0] ← -1;
for (i ← 0, j ← -1; i < M; i ← i + 1, j ← j + 1) do {
next[i] ← j;
while ((j ≥ 0) and (p[i] ≠ p[j])) do
j ← next[j];
}
end InitNext()
next[i]는 주어진 문자열의 0~(i-1) 까지의 부분 문자열 중에서 prefix == suffix가 될 수 있는 부분 문자열 중에서 가장 긴 것의 길이이다.

KMP(p[], t[])
M ← 패턴의 길이; N ← 텍스트의 길이;
InitNext(p);
for (i ← 0, j ← 0; j < M and i < N; i ← i + 1, j ← j + 1) do
while ((j ≥ 0) and (t[i] ≠ p[j])) do
j ← next[j];
if (j = M) then return i - M;
else return i;
end KMP()전처리해둔 패턴을 이용한 KMP 알고리즘 실행과정이다.

KMP는 패턴을 이용하여 탐색을 진행하는데 이때 패턴을 더 단순화 시키는 방법을 이용할 수 있다. 우선 패턴을 유한 상태 장치(finite state machine: FSM)로 표현을 해보고 더 단순한 패턴으로 만드는 과정을 살펴보자.

어짜피 다음으로 넘어가야하는 경우에는 미리 끝까지 넘겨서 연결을 지어놓는 간단한 알고리즘이다.
if (p[i] == p[j]) then next[i] ← next[j];
else next[i] ← j
10100111에서의 예시를 좀더 자세히 살펴보면 아래와 같다.
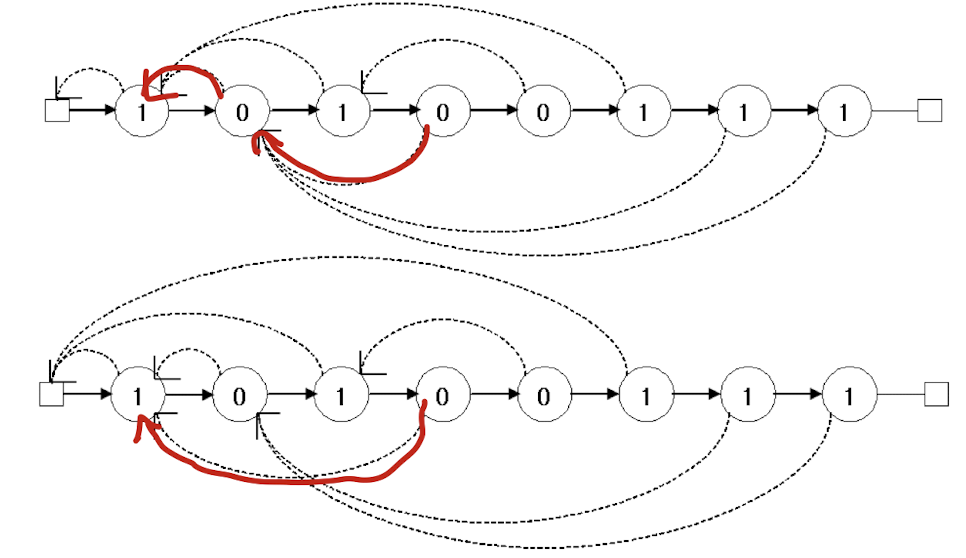
표시된 부분을 보면 0으로 검사를 했을때 틀려서 next[4]에서 next[2]로 넘어가고 틀리면 다시 next[1]로 넘어가는데 해당 노드의 수를 보면 0으로 같기 때문에 당연히 연속해서 틀릴 수 밖에없다. 따라서 두번거치지 않고 한번에 next[4]에서 next[1]으로 넘어가도록 패턴을 단순화 시켜놓는 것이다.
개선된 FSM을 이용하여 KMP 알고리즘을 진행하니 다음과 같이 좀더 빨라지는 모습이다.

BM
BM 알고리즘은 보이어-무어 알고리즘을 간단히 부르는 이름이다. 이 알고리즘은 오른쪽에서 왼쪽으로 스트링 탐색을 진행하고 불일치 문자 방책(mismatched character heuristic)을 사용한다. 불일치 문자 방책은 텍스트에 있는 불일치가 발생한 문자가 패턴의 문자가 일치하도록 패턴을 오른쪽으로 이동시키는 것이다.
또한 일치 접미부 방책(good suffix heuristic)을 사용하는데 이는 패턴에서 불일치가 발생한 문자의 오른쪽에 있는 최대 접미부가 일치하도록 패턴을 오른쪽을 이동시키는 것이다.
두 방법 중 패턴을 우측으로 이동하는 거리가 더 긴 것을 선택한다. 이동하는 거리가 더 길다는 것은 해당 알고리즘은 이동하는 거리만큼을 모두 검증하여 문제가 발생할 것으로 분석을 하였다는 것이므로 false start 횟수를 감소시킬 수 있다.
최선의 경우 시간 복잡도는 O(m + n /m + |Σ|)이 된다. 알파벳이 큰 경우 해당 시간 복잡도내에 수행될 가능성이 매우 높아진다.
두 핵심 알고리즘을 살펴보면 아래와 같다.

불일치 문자 방책 알고리즘부터 상세히 살펴보자.
void InitSkip(char *p)
{
int i, M = strlen(p);
for (i = 0; i < NUM; i++) skip[i] = M;
for (i = 0; i < M; i++) skip[index(p[i])] = M - i - 1;
}
위의 skip배열을 이용하여 BM알고리즘을 진행한다. 위와 같은 skip 배열의 숫자는 만약 텍스트가 일치하지 않을 경우 얼마만큼 건너뛰어야 하는지 표시한 것이다.
MisChar(p[], t[])
M ← 패턴의 길이; N ← 텍스트의 길이;
InitSkip(p);
for (i ← M-1, j ← M-1; j ≥ 0; i ← i - 1, j ← j - 1) do
while (t[i] ≠ p[j]) do {
k ← skip[index(t[i])];
if (M-j > k) then i ← i + M - j;
else i ← i + k;
if (i ≥ N ) then return N;
j ← M - 1;
}
return i+1;
end MisChar()코드를 보면 알 수 있지만 건너뛰는 숫자는 정해진 패턴인 k만큼일 수도 있지만 M-j 즉 (패턴의 길이 - 현재 탐색중인 패턴의 인덱스 번호)가 k보다 크면 M-j만큼 이동한다. 따라서 k=0인 케이스 아래에서는 N을 마주치고 오답인 경우에 제자리에서 탐색을 하는 것이 아니라 M-j만큼 이동을 시키는 것이다.
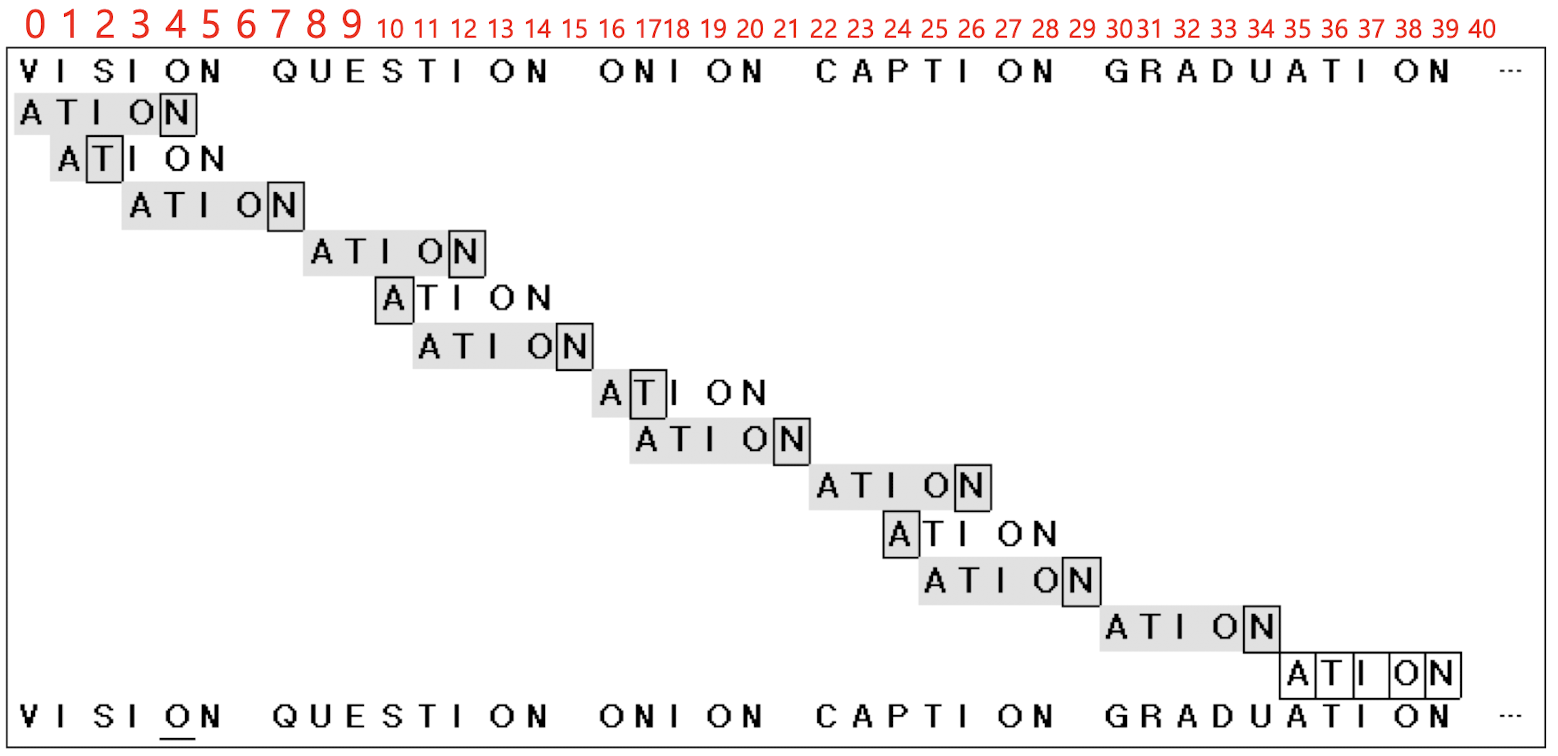
첫줄부터 조금 살펴보자. N과 O가 일치 하지 않으니 O의 skip number인 1만큼 pattern을 오른쪽으로 옮긴다. N, O, I까지는 일치하지만 T와 S가 일치하지 않고 S는 패턴에 존재하지 않는 값이므로 S위치로부터 skip number인 5만큼 오른쪽으로 옮긴다. 중간에 ONION을 만났을때 위에서 말한 M-j만큼 이동하는 경우가 나온다. T는 1번 인덱스이고 패턴의 길이는 5기 때문에 5-1 즉 N위치인 17로부터 4만큼 이동시켜서 21에 패턴의 끝이 옮겨지는 것을 볼 수 있다. 이러한 조건을 따져주며 과정을 반복하여 pattern으로 오른쪽으로 옮기다가 ATION을 만나서 스트링 검색을 끝마치는 모습이다.
'Univ. Study > Algorithm Design' 카테고리의 다른 글
| 알고리즘 설계 실습 - KMP (0) | 2024.04.17 |
|---|---|
| Algorithm Design - 라빈-카프 / 패턴 매칭 (0) | 2024.04.17 |
| Algorithm Design - B-Tree / B+Tree (0) | 2024.04.05 |
| Algorithm Design - Tree (0) | 2024.04.04 |
| 알고리즘 설계 실습 - 트리 순환 (1) | 2024.04.03 |



