Rabin-Karp
라빈-카프 알고리즘은 스트링을 숫자값으로 바꾼 다음 해시 값을 계산하여 매칭하는 알고리즘이다. 최악의 시간 복잡도는 O(MN)이지만 평균적으로는 선형에 가까운 빠른 속도를 가지는 알고리즘이다. 첫 번째 M 자리의 나머지를 구한 다음부터는 한 자리씩만 추가하면서 간단한 계산으로 나머지를 구할 수 있으므로 빠른 시간에 스트링 탐색을 수행한다.

해시 값이 다르다면 두 문자열이 다르다는 것이 보장된다.

그러나 해시 값이 같다고 해서 두 문자열이 같다는 것이 보장되지는 않기 때문에 해시값이 같은 경우 문자열을 비교하는 과정을 거친다.

찾고자하는 패턴은 한번 연산을 해두면 해시값이 정해져있지만 한칸씩 넘어가며 텍스트와 비교를 할때 텍스트에서 비교하고자 하는 부분의 해시값을 매번 다시 연산하는 것은 연산량이 너무 낭비된다. 이를 개선하기 위해 아래의 수학적 특징을 이용한다.
P[m]이라는 패턴은 아래와 같이 표현할 수 있다.


modula 연산은 아래와 같은 성질이 있다.

위의 방법을 이용하면 31415mod13은 아래와 같은 방법으로 연산될 수 있다.

31415mod13 = 7

위와 같은 문자열이 있을때 한칸 오른쪽으로 이동한 문자열은 아래와 같이 표현된다.

이 특징을 이용하면 연산을 재활용하여 오른쪽으로 이동한 문자열의 해시 값을 쉽게 구할 수 있다.

구체적인 예시를 통해 살펴보면 아래와 같다.

31415에서 구해놓은 31415mod13=7이라는 값을 이용하여 옆으로 한칸만 변환하여 간단한 mod연산으로 14152를 구해내는 모습이다.
라빈-카프 알고리즘의 수도코드이다.
RabinKarp(p[], t[])
dM ← 1; h1 ← 0; h2 ← 0;
M ← 패턴의 길이; N ← 텍스트의 길이;
for (i ← 1; i < M; i ← i + 1) do
dM ← (d*dM) mod q;
for (i ← 0; i < M; i ← i + 1) do {
h1 ← (h1 * d + index(p[i])) mod q;
h2 ← (h2 * d + index(t[i])) mod q;
}
for (i ← 0; h1 ≠ h2; i ← i + 1) do {
h2 ← (h2 + d * q - index(t[i]) * dM) mod q;
h2 ← (h2 * d + index(t[i+M])) mod q;
if (i > N-M) then return N;
}
return i;
end RabinKarp()
패턴 매칭 알고리즘
패턴 매칭 알고리즘은 텍스트 스트링에서 원하는 문자 패턴을 찾아내는 것이다. 패턴 기술로는 크게 3가지 정도가 있다.
1. 접합(concatenation)
패턴에서 인접해 있는 두 문자가 텍스트에서 나타나면 매치
2. 논리합(or)
두 개의 문자 중 하나가 텍스트에 나타나면 매치
3. 폐포(closure)
특정한 문자가 0개 이상 나타나면 매치

정규식(regular expression)은 정한 규칙을 가진 문자열의 집합을 표현하는 데 사용하는 형식 언어이다.
자주 쓰이는 심볼(symbol)은 다음과 같은 것들이 있다.
* : 괄호 안에 있는 문자들이 0번 이상 나타남
? : 어떤 문자와도 매치됨
+ : 또는(or)의 역할
예시
?*(ie+ei)?*: ie 또는 ei를 가지고 있는 모든 단어(n개의 아무 문자가 ie 또는 ei 앞,뒤에 나타나는 형식)
(1+01)*(0+1) : 연속적으로 두 개의 0이 나오지 않는 0과 1로 이루어진 모든 스트링(1 또는 01의 n회 반복후에 0 또는 1이 추가된 형식)
패턴 매칭 장치(pattern matching machine)은 비결정적 장치인데 결정적 장치와 비결정적 장치에 대해 간단히 살펴보면 아래와 같다.
- 결정적(deterministic) 장치
• 각각의 상태 전이가 다음 입력 문자에 의해 완전하게 결정 되는 방식으로 작동한다.
• 예: KMP알고리즘을 위한 유한 상태 장치
- 비결정적(nondeterministic) 장치
• 패턴을 매치하기 위해 하나 이상의 방법이 있을 경우 장치가 올바른 것을 찾아나가는 방식으로 작동한다.
• 텍스트 스트링에서 (A*B+AC)D와 같은 정규식을 찾는 경우 사용되며, 유일한 시작 상태와 종료 상태를 가진다.
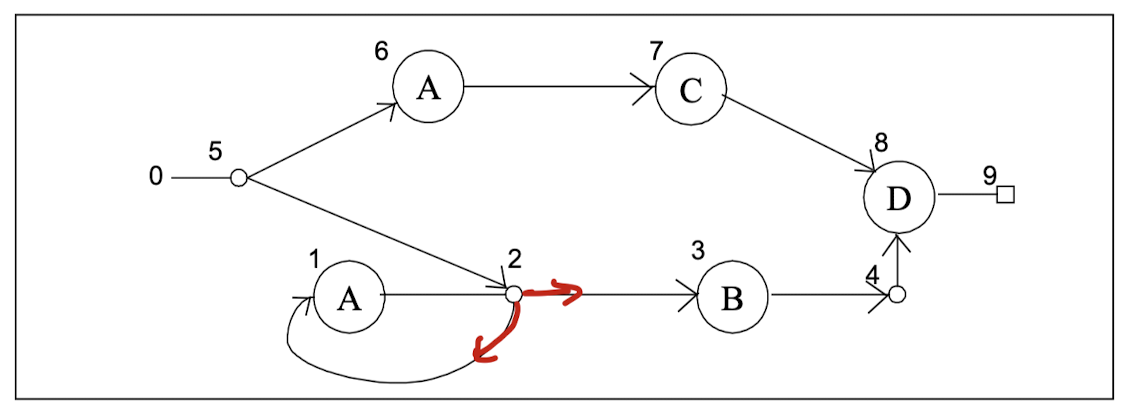
위는 (A*B+AC)D를 위한 비결정적 패턴 매칭 장치를 도식화한 것이다. 이를 배열로 표현하면 아래와 같다.

패턴 매칭 장치를 구현하는데 가장 적합한 자료구조는 데크(deque: double-ended queue)이다. 스택과 큐의 특징을 조합한 자료구조로원래는 양방향에서 항목을 추가하고 삭제하는 것이 가능하나 패턴매칭 장치 구현을 위한 데크는 입력은 양방향에서 가능하고 삭제는 데크의 처음에서만 가능한 출력-제한 데크(output-restricted deque)로 사용한다.

N 문자로 이루어진 텍스트 스트링에서 M-상태 장치가 패턴을 찾는 것은 최악의 경우에도 NM 번 이하의 상태 전이만이 필요하다.
아래와 같은 과정으로 장치가 동작하고 패턴 매칭을 진행한다.
1. 문자가 매치됨 → 새로운 상태를 데크의 끝에 삽입(insertLast)
2. 상태가 비어 있음 → 두 개의 가능한 상태를 데크의 처음에 삽입(insertFirst)
3. scan을 만남→입력 스트링에 대한 포인터를 다음 문자로 이동

순차적으로 다음 가능성을 +아래에 넣어두고 하나씩 체크하며 일치하는지 확인하고 두가지 케이스가 가능하다면 두가지 가능성을 모두 살려두고 지속적으로 체크하다가 가능한 경우만 남겨가며 순차적으로 진행하면 된다.
'Univ. Study > Algorithm Design' 카테고리의 다른 글
| Algorithm Design - Huffman encoding / Encryption / RSA (1) | 2024.04.18 |
|---|---|
| 알고리즘 설계 실습 - KMP (0) | 2024.04.17 |
| Algorithm Design - 스트링 탐색 알고리즘(Naïve/KMP/BM) (0) | 2024.04.12 |
| Algorithm Design - B-Tree / B+Tree (0) | 2024.04.05 |
| Algorithm Design - Tree (0) | 2024.04.04 |



