Selection Sort
선택정렬(Selection Sort)은 배열(array)을 정렬할 때 가장 간단한 방법 중 하나이다. 이 알고리즘은 배열을 처음부터 끝까지 반복하면서 가장 작은 값을 찾아서 배열의 맨 앞에 위치시키는 과정을 반복하는 방식으로 동작한다.

이전에 다루었었기 때문에 정렬알고리즘은 간단하게 그림으로 설명하고 넘어간다.
SelectionSort Psuedo code
SelectionSort(A) // A는 배열
n = A.length // 배열의 길이를 구합니다.
for i = 0 to n-1 do // 첫 번째 인덱스부터 끝까지 반복합니다.
minIndex = i // 가장 작은 값의 인덱스를 저장할 변수를 초기화합니다.
for j = i+1 to n do // i 다음 인덱스부터 끝까지 반복합니다.
if A[j] < A[minIndex] then // 현재까지 찾은 가장 작은 값보다 더 작은 값을 찾으면
minIndex = j // 인덱스를 업데이트합니다.
temp = A[i] // 선택한 인덱스의 값을 temp 변수에 저장합니다.
A[i] = A[minIndex] // 선택한 인덱스에 가장 작은 값으로 교체합니다.
A[minIndex] = temp // 가장 작은 값의 자리에 선택한 값을 넣어줍니다.
return A // 정렬된 배열을 반환합니다.위의 의사 코드를 보면, 선택정렬은 두 개의 반복문을 사용하여 배열의 모든 원소를 비교하면서 정렬하는 것을 알 수 있다. 이 알고리즘의 시간 복잡도는 O(n^2)이다.
Bubble Sort
버블정렬(Bubble Sort)은 두 개의 인접한 원소를 비교하면서 정렬하는 알고리즘 중 하나이다. 배열의 처음부터 끝까지 반복하면서 인접한 두 개의 원소를 비교하고, 필요한 경우 위치를 교환하는 과정을 반복하여 정렬하는 방식으로 동작한다.

BubbleSort Psuedo code
BubbleSort(A) // A는 배열
n = A.length // 배열의 길이를 구합니다.
for i = 0 to n-1 do // 첫 번째 인덱스부터 끝까지 반복합니다.
for j = 0 to n-i-1 do // 배열의 끝까지 반복합니다.
if A[j] > A[j+1] then // 다음 인덱스의 값이 현재 인덱스의 값보다 작으면
temp = A[j] // 두 원소의 위치를 교환합니다.
A[j] = A[j+1]
A[j+1] = temp
return A // 정렬된 배열을 반환합니다.위의 의사 코드를 보면, 버블정렬도 선택정렬과 마찬가지로 두 개의 반복문을 사용하여 배열의 모든 원소를 비교하면서 정렬하는 것을 알 수 있다. 이 알고리즘의 시간 복잡도는 O(n^2)이다.

정렬여부를 확인하는 코드를 추가하여 Bubble Sort 알고리즘을 개선할 수 있다.
개선된 알고리즘의 경우 이미 정렬된 배열은 O(n) 시간복잡도로 해결이 가능하다.
Insertion Sort
삽입정렬(Insertion Sort)은 정렬되지 않은 부분의 원소를 하나씩 이미 정렬된 부분의 적절한 위치에 삽입하면서 정렬하는 알고리즘이다. 배열의 길이가 작을 때나 이미 정렬된 배열에 새로운 원소를 추가하는 경우에 유용하다.

InsertionSort Psuedo code
InsertionSort(A) // A는 배열
n = A.length // 배열의 길이를 구합니다.
for i = 1 to n-1 do // 첫 번째 원소는 이미 정렬되었다고 가정하므로 두 번째 원소부터 반복합니다.
key = A[i] // 선택한 원소를 key 변수에 저장합니다.
j = i-1 // 이미 정렬된 부분의 끝 인덱스를 저장합니다.
while j >= 0 and A[j] > key do // 이미 정렬된 부분에서 key보다 큰 원소를 찾을 때까지 반복합니다.
A[j+1] = A[j] // 원소를 오른쪽으로 한 칸 이동합니다.
j = j-1 // 인덱스를 왼쪽으로 이동합니다.
A[j+1] = key // key를 해당 위치에 삽입합니다.
return A // 정렬된 배열을 반환합니다.위의 의사 코드를 보면, 삽입정렬은 이미 정렬된 부분과 정렬되지 않은 부분을 구분하여 처리하는 것을 알 수 있다. 이 알고리즘의 시간 복잡도는 O(n^2)이다. 따라서 배열의 크기가 커지면 성능이 저하될 수 있다. 하지만 배열이 거의 정렬되어 있는 경우에는 효율적인 알고리즘이 될 수 있다. 따라서 새로운 수를 추가하여 다시 정렬할때 효율이 올라간다.
Merge Sort
병합정렬(Merge Sort)은 분할 정복(Divide and Conquer) 방법을 사용하여 배열을 정렬하는 알고리즘이다. 배열을 반으로 나누어 각각을 재귀적으로 정렬한 후, 두 개의 정렬된 배열을 병합하여 최종적으로 정렬된 배열을 얻는다. 이 알고리즘은 안정적인 정렬 알고리즘이며, 항상 O(nlogn)의 시간 복잡도를 보장한다.

Merge 과정
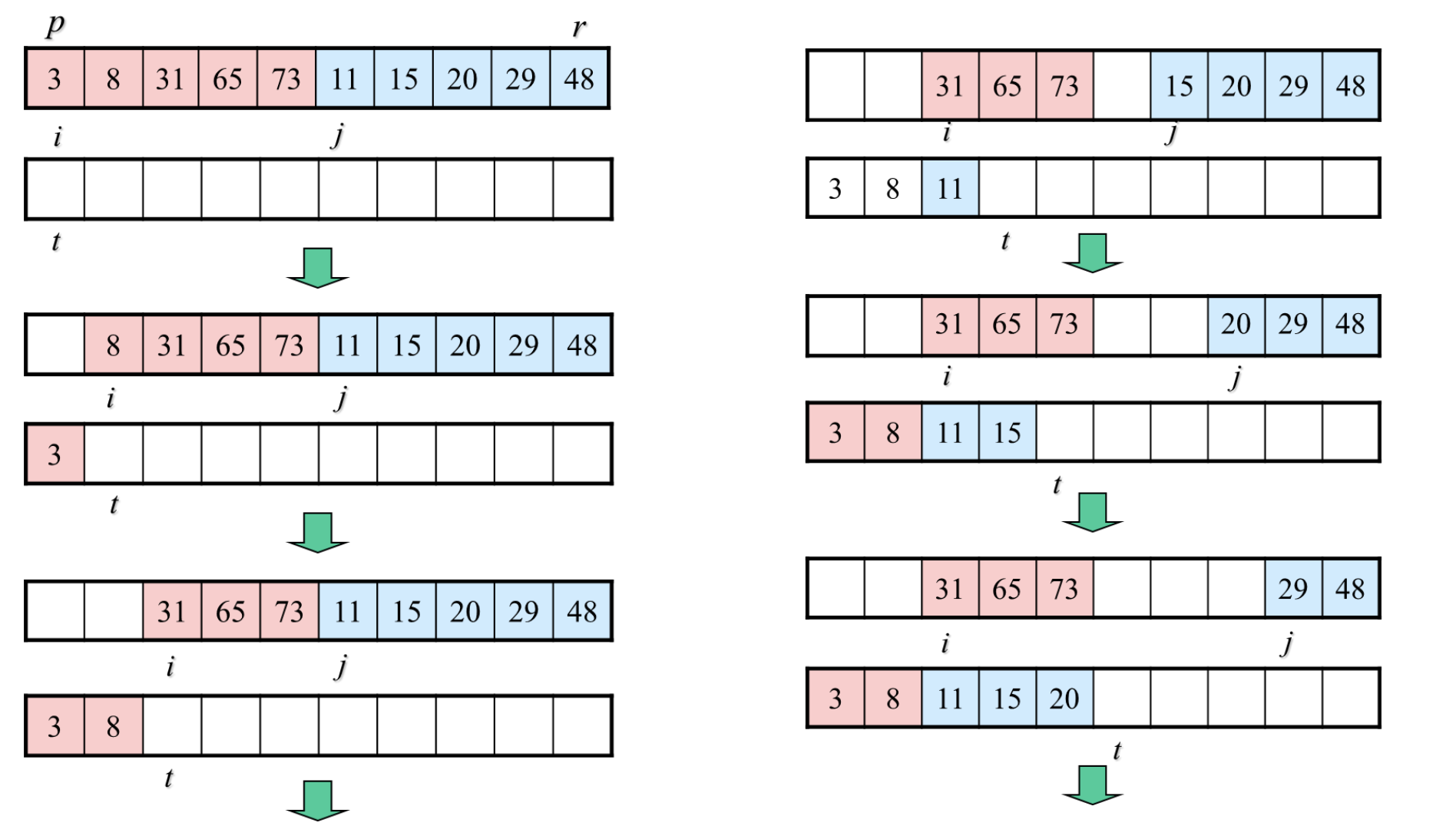
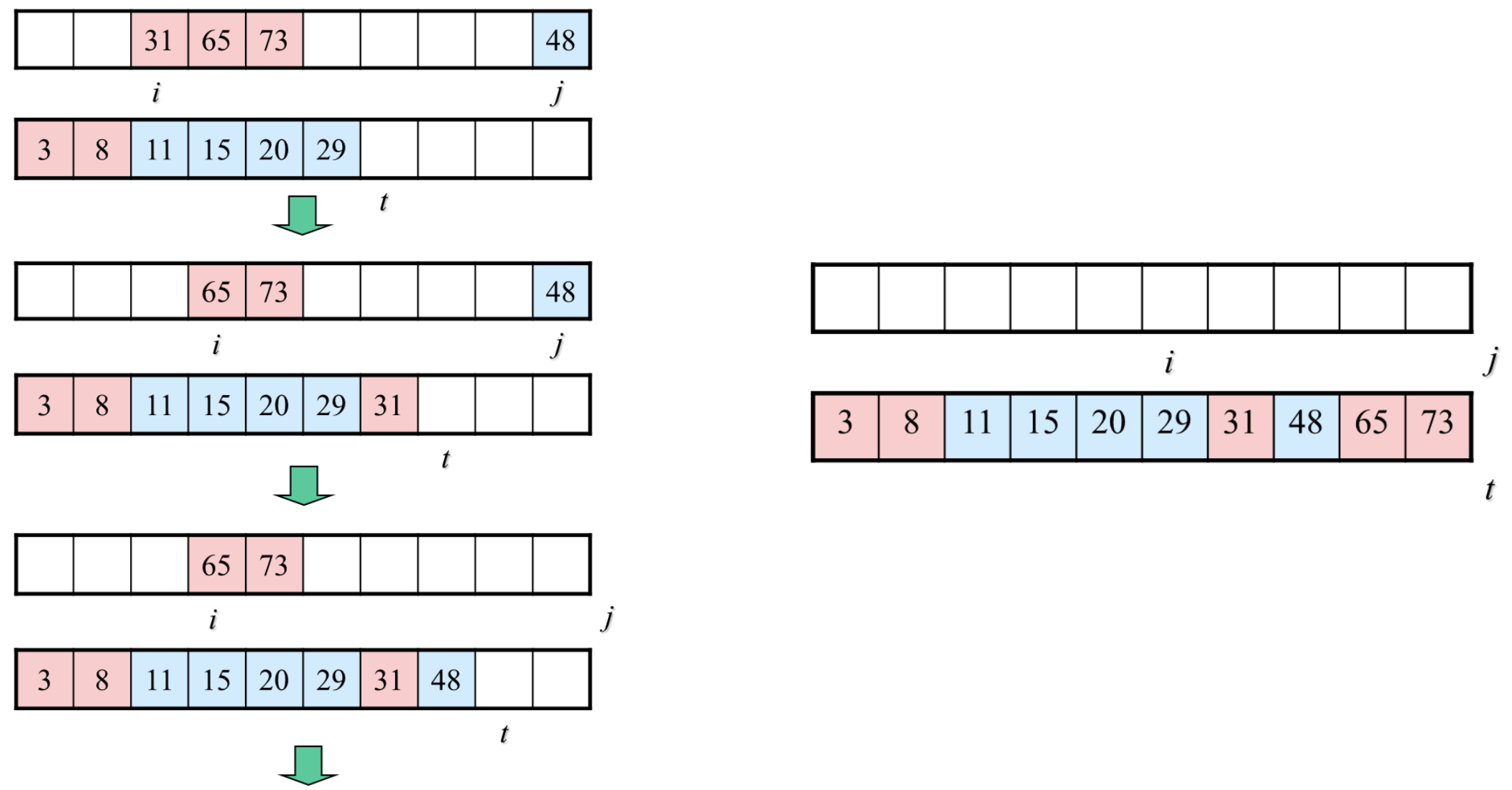
MergeSort Psuedo code
MergeSort(A, p, r) // A는 배열, p는 시작 인덱스, r은 끝 인덱스
if p < r then // 배열의 크기가 1보다 큰 경우
q = (p+r) / 2 // 배열을 반으로 나누는 인덱스를 계산합니다.
MergeSort(A, p, q) // 배열의 왼쪽 절반을 정렬합니다.
MergeSort(A, q+1, r) // 배열의 오른쪽 절반을 정렬합니다.
Merge(A, p, q, r) // 두 개의 정렬된 배열을 병합합니다.
Merge(A, p, q, r)
n1 = q-p+1 // 왼쪽 배열의 크기를 구합니다.
n2 = r-q // 오른쪽 배열의 크기를 구합니다.
L[1...n1+1]과 R[1...n2+1]을 생성합니다. // 임시 배열을 생성합니다.
for i = 1 to n1 do // 왼쪽 배열의 원소를 복사합니다.
L[i] = A[p+i-1]
for j = 1 to n2 do // 오른쪽 배열의 원소를 복사합니다.
R[j] = A[q+j]
L[n1+1] = ∞ // 두 개의 배열의 끝을 표시하는 값을 추가합니다.
R[n2+1] = ∞
i = 1 // 왼쪽 배열에서 비교할 원소의 인덱스를 저장합니다.
j = 1 // 오른쪽 배열에서 비교할 원소의 인덱스를 저장합니다.
for k = p to r do // 결과 배열에 정렬된 원소를 추가합니다.
if L[i] <= R[j] then // 두 배열에서 더 작은 값을 결과 배열에 추가합니다.
A[k] = L[i]
i = i + 1
else
A[k] = R[j]
j = j + 1Quick Sort
퀵 정렬(Quick Sort)은 분할 정복(divide and conquer) 알고리즘을 기반으로 한 정렬 알고리즘으로, 평균적으로 가장 빠른 속도를 가지는 알고리즘 중 하나입니다.
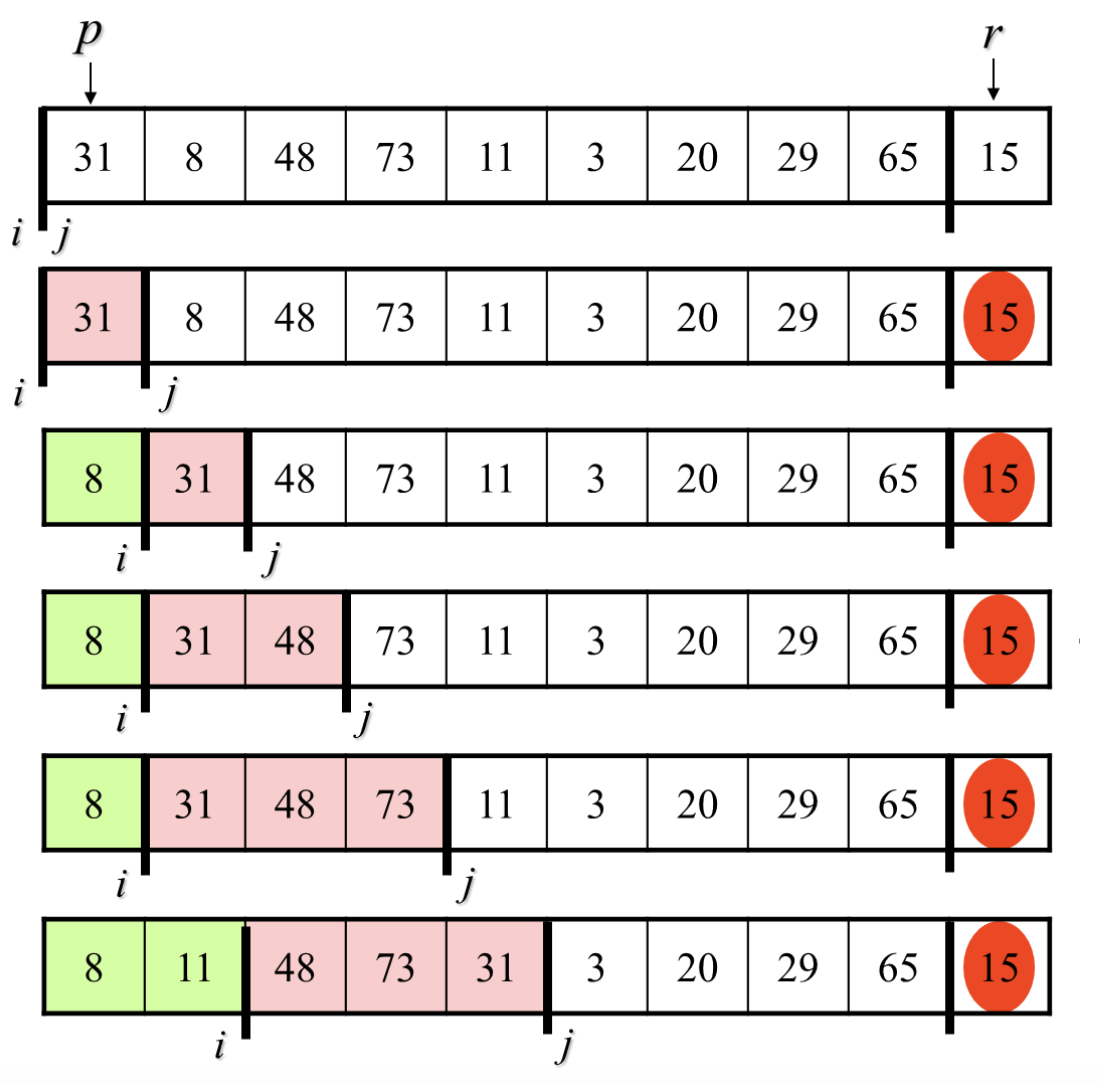
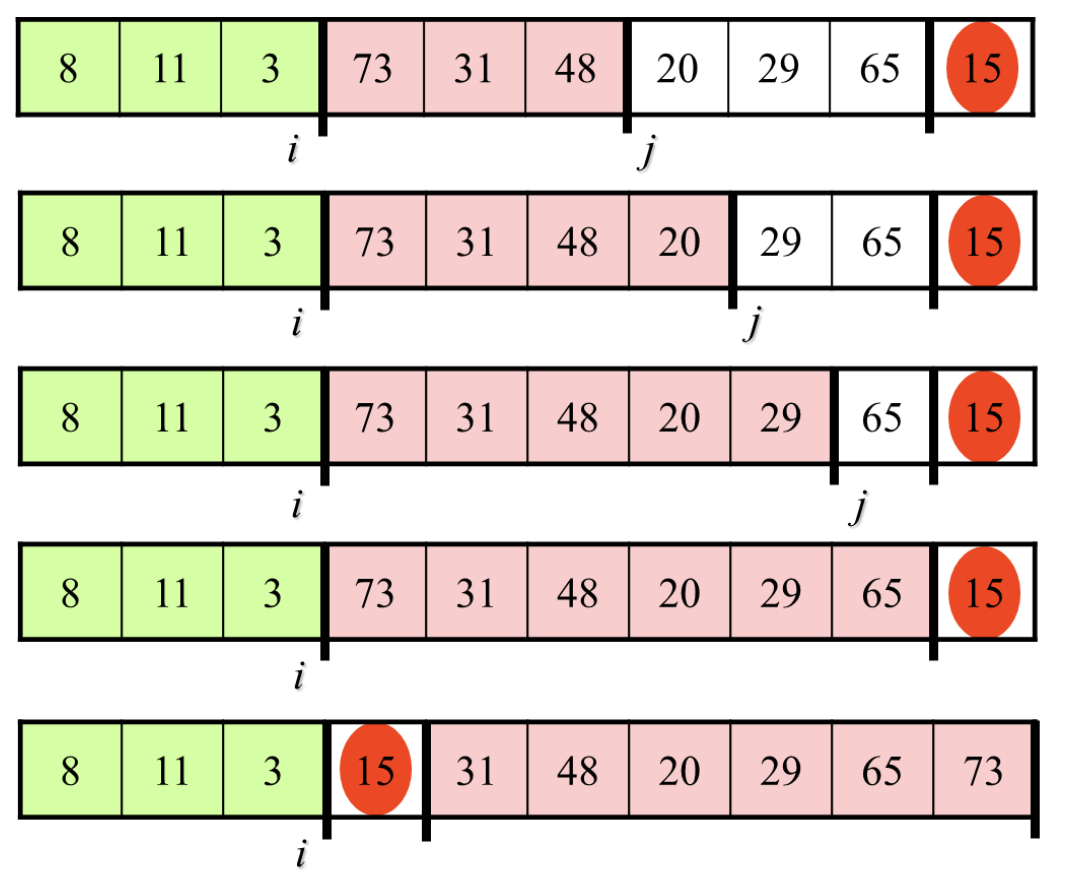
QuickSort Psuedo code
QuickSort(A, low, high)
if low < high then
pivot = Partition(A, low, high) // 배열을 분할하여 기준을 정하고, 기준의 인덱스를 반환합니다.
QuickSort(A, low, pivot-1) // 기준의 왼쪽 부분 배열에 대해 재귀적으로 퀵 정렬을 수행합니다.
QuickSort(A, pivot+1, high) // 기준의 오른쪽 부분 배열에 대해 재귀적으로 퀵 정렬을 수행합니다.
Partition(A, low, high)
pivot = A[high] // 마지막 요소를 기준으로 설정합니다.
i = low-1 // i 변수는 pivot보다 작은 값을 저장하기 위한 인덱스입니다.
for j = low to high-1 do // j 변수는 pivot보다 큰 값을 찾기 위한 인덱스입니다.
if A[j] < pivot then
i = i+1
swap(A[i], A[j]) // A[i]와 A[j]를 교환합니다.
swap(A[i+1], A[high]) // A[i+1]과 pivot을 교환합니다.
return i+1 // 기준의 인덱스를 반환합니다.MergeSort VS QuickSort
병합 정렬과 퀵 정렬은 모두 분할 정복(divide and conquer) 알고리즘을 기반으로 하며, 평균적으로 O(nlogn)의 시간 복잡도를 가지는 빠른 정렬 알고리즘이다. 하지만, 두 알고리즘의 성능은 상황에 따라 다를 수 있다.
먼저, 병합 정렬의 경우 분할(divide) 과정에서 데이터를 반으로 나누는 것이고, 합병(merge) 과정에서는 두 개의 배열을 비교하면서 작은 값을 새로운 배열에 저장하는 과정이다. 이러한 과정으로 인해, 병합 정렬은 분할된 두 개의 배열의 크기가 같은 경우와 같은 크기로 분할하는 경우 가장 빠르게 동작한다. 하지만, 데이터가 이미 정렬된 경우에도 두 개의 배열을 합병하는 과정에서 값이 바뀌지 않기 때문에 쓸데없는 계산이 발생하게 되어 성능이 떨어지게 된다.
반면, 퀵 정렬은 배열을 기준(pivot)을 기준으로 작은 값은 왼쪽으로, 큰 값은 오른쪽으로 분할하는 과정을 반복한다. 퀵 정렬에서는 분할된 배열의 크기가 항상 절반으로 나누어지는 것이 아니므로, 분할 과정에서 최악의 경우 O(n^2)의 시간 복잡도를 가질 수 있다. 그러나, pivot을 잘 선택하면 평균적으로 O(nlogn)의 시간 복잡도를 가지며, 데이터가 이미 정렬된 경우에도 빠른 속도를 보인다.
컴퓨터 구조와 캐시(Cache) 관점에서 병합 정렬과 퀵 정렬의 성능을 비교하면, 이들의 차이는 메모리 접근 패턴(memory access pattern)에 있다.
병합 정렬은 분할된 배열의 작은 부분 배열들을 반복적으로 메모리에서 가져와서 비교하고, 새로운 배열에 복사하는 작업을 한다. 이러한 과정에서 배열의 일부분만 사용하므로, 메모리에서 가져오는 데이터가 캐시에 저장되어 있지 않을 가능성이 높다. 이러한 상황에서는 캐시 미스(cache miss)가 자주 발생하여 메모리 접근 시간이 상당히 느려질 수 있다.
반면, 퀵 정렬은 배열을 작은 부분 배열로 나누는 과정에서 pivot을 기준으로 작은 값은 왼쪽으로, 큰 값은 오른쪽으로 이동시키며, 각각의 부분 배열에 대해 동일한 작업을 수행한다. 이러한 작업에서는 부분 배열의 데이터를 순차적으로 읽어야 하므로, 캐시에 데이터가 미리 적재되어 있을 확률이 높다. 이러한 이유로, 퀵 정렬에서는 캐시 미스가 상대적으로 적게 발생하므로 메모리 접근 시간이 빠르다.
따라서, 병합 정렬과 퀵 정렬 중에서 어느 알고리즘이 더 좋은 성능을 보일지는 컴퓨터 구조와 캐시의 크기, 메모리 접근 패턴 등 여러 가지 요소에 따라 달라진다. 일반적으로, 병합 정렬은 큰 배열을 정렬하는 경우에, 퀵 정렬은 작은 배열이나 중간 정도의 크기의 배열을 정렬하는 경우에 성능이 더 좋다.
반면 일반적으로 데이터 사이즈가 큰 경우에는 병합 정렬이 유리하다.
이는 병합 정렬의 성능이 입력 데이터의 크기에 비례해서 증가하기 때문이다. 즉, 병합 정렬은 입력 데이터를 계속해서 작은 조각으로 나누어 정렬하고, 이 조각들을 병합하는 과정에서 정렬을 수행한다. 이 과정에서 입력 데이터의 크기가 크더라도 작은 조각으로 나누어서 정렬하므로, 정렬 알고리즘의 시간 복잡도가 적어지게 된다.
반면, 퀵 정렬의 경우 입력 데이터의 크기가 커질수록 pivot을 선택하는 과정에서 최악의 경우 시간 복잡도가 O(n^2)까지 증가할 수 있다. 따라서, 퀵 정렬은 입력 데이터가 작을 때는 빠른 속도를 보이지만, 데이터 사이즈가 커질수록 불안정해지며 병합 정렬보다 느리게 동작할 가능성이 높다.
따라서, 대부분의 경우에는 데이터 사이즈가 큰 경우에는 병합 정렬을 사용하는 것이 좋다.
'Quality control (Univ. Study) > Algorithm Design' 카테고리의 다른 글
| Lecture 13 - 집합의 처리 (0) | 2023.04.10 |
|---|---|
| Lecture 11 - 해시 테이블 (0) | 2023.04.03 |
| Lecture4 - 점화식과 점근적 복잡도 분석 (0) | 2023.03.08 |
| Lecture3 - 알고리즘 설계와 분석의 기초(2) (1) | 2023.03.06 |
| Lecture1,2 - 알고리즘 설계와 분석의 기초(1) (0) | 2023.03.05 |



