상호 배타적 집합
상호 배타적 집합은 서로 공유하는 원소가 없는 여러 집합들의 모임 (disjoint sets)으로 각 집합은 대표 원소로써 해당 집합을 나타낸다.
관련 연산을 보면 다음과 같다.
▪ Make-Set(𝑥) : 원소 𝑥로만 이루어진 집합을 생성
▪ Find-Set(𝑥) : 원소 𝑥가 포함된 집합을 찾은 후 대표 원소에 대한 포인터를 반환
▪ Union(𝑥, 𝑦) : 원소 𝑥가 포함된 집합과 원소 𝑦가 포함된 집합을 합쳐서 합집합 생성
시간 복잡도 분석 관련하여 총 𝑚회의 Make-Set, Find-Set, Union 연산이 있을 때 𝑛번의 MakeSet 연산이 포함된 상황을 가정한다.
대표적으로 그래프 구조에서의 connected component 관련 처리에 활용된다.


연결 리스트를 이용한 집합의 처리
같은 집합의 원소들은 하나의 연결 리스트로 관리하며, 연결 리스트 맨 앞의 원소를 집합의 대표 원소로 삼는다. 또한 모든 원소들은 대표 원소에 대한 포인터를 갖고 있다.

대표원소를 결정하는 방식은 복잡한 과정이 있지만 다루기 어려워 우선 맨 앞의 원소를 대표원소로 잡고 수행하는 과정을 본다.
Make-Set(𝑥) - 원소 𝑥를 저장하는 노드를 하나 생성한 후 대표 노드로는 자기 자신을 가리키도록 하고, 다음 원소에 대한 포인터는 NIL로 설정한다.
Find-Set(𝑥) - 원소 𝑥가 포함된 노드에서 대표 노드에 대한 포인터를 반환한다.
Union(𝑥, 𝑦) - 원소 𝑥가 포함된 리스트와 원소 𝑦가 포함된 리스트를 합치고, 더 뒤쪽에 오는 리스트의 경우 각 노드에서의 대표 노드를 새로운 대표 노드로 변경한다.
가장 난이도가 있는 Union(x,y)의 예시를 보자.

만약 𝑛개의 노드를 새로 생성하여 모두 합친다면 Θ(𝑛^2)의 시간 복잡도로 수행이 가능하다. Union 연산은 더 긴 쪽에서 대표 노드를 모두 바꿔주어야 할 수 있으므로 Θ(𝑛)의 평균 시간 복잡도를 가진다.

무게를 고려한 Union (Weighted-Union)
Union 연산을 수행할 때, 두 리스트의 길이를 비교한 후 항상 같거나 더 짧은 쪽을 뒤에 붙이는 Union 연산으로 무게를 고려한 Union을 사용하더라도 여전히 Union 연산 자체는 Ω(𝑛)이다.

Make-Set 및 Find-Set은 𝑂(1)이고 이 둘을 합쳐도 𝑚을 넘지 않으므로, 합쳐서 𝑂(𝑚)으로 둘 수 있다. Union은 리스트를 연결하는 작업은 𝑂(1)이지만 대표 노드를 갱신하는 과정은 더 오래 걸릴 수 있다. 넉넉하게 잡으면 Union 한 번의 시간 복잡도가 𝑂(𝑛)이지만 더욱 타이트하게 설정이 가능하다. 어떠한 원소 𝑥에 대해 Union에 의해 발생하는 대표 노드 갱신 횟수를 살펴보자. 𝑥가 포함된 리스트가 Union 연산에서 같거나 더 짧은 리스트일 때만 갱신이 발생한다. 그리고 𝑥가 포함된 리스트에서 대표 노드 갱신이 발생했다면, 같거나 더 짧은 리스트였기 때문에 𝑥가 포함된 리스트의 길이 는 2배 이상 커지게 된다. 또한, 리스트는 아무리 길어도 𝑛을 넘기지 않는다. (Make-Set 횟수=총 원소 수=𝑛)
따라서, 원소 𝑥에 대한 대표 노드 갱신 횟수는 아무리 많아도 [log_2 𝑛]번 가능하다. 원소의 총 개수가 𝑛개 이므로 대표 노드 갱신의 총 횟수는 [𝑛log_2 𝑛] 이 된다. 즉, 전체 시간은 𝑂(𝑚 + 𝑛 log 𝑛)이 된다.
트리를 이용한 집합의 처리
같은 집합의 원소들을 하나의 트리로 관리하며 트리의 루트를 대표 원소로 삼는다. Disjoint-set forests라고 부르기도 한다.
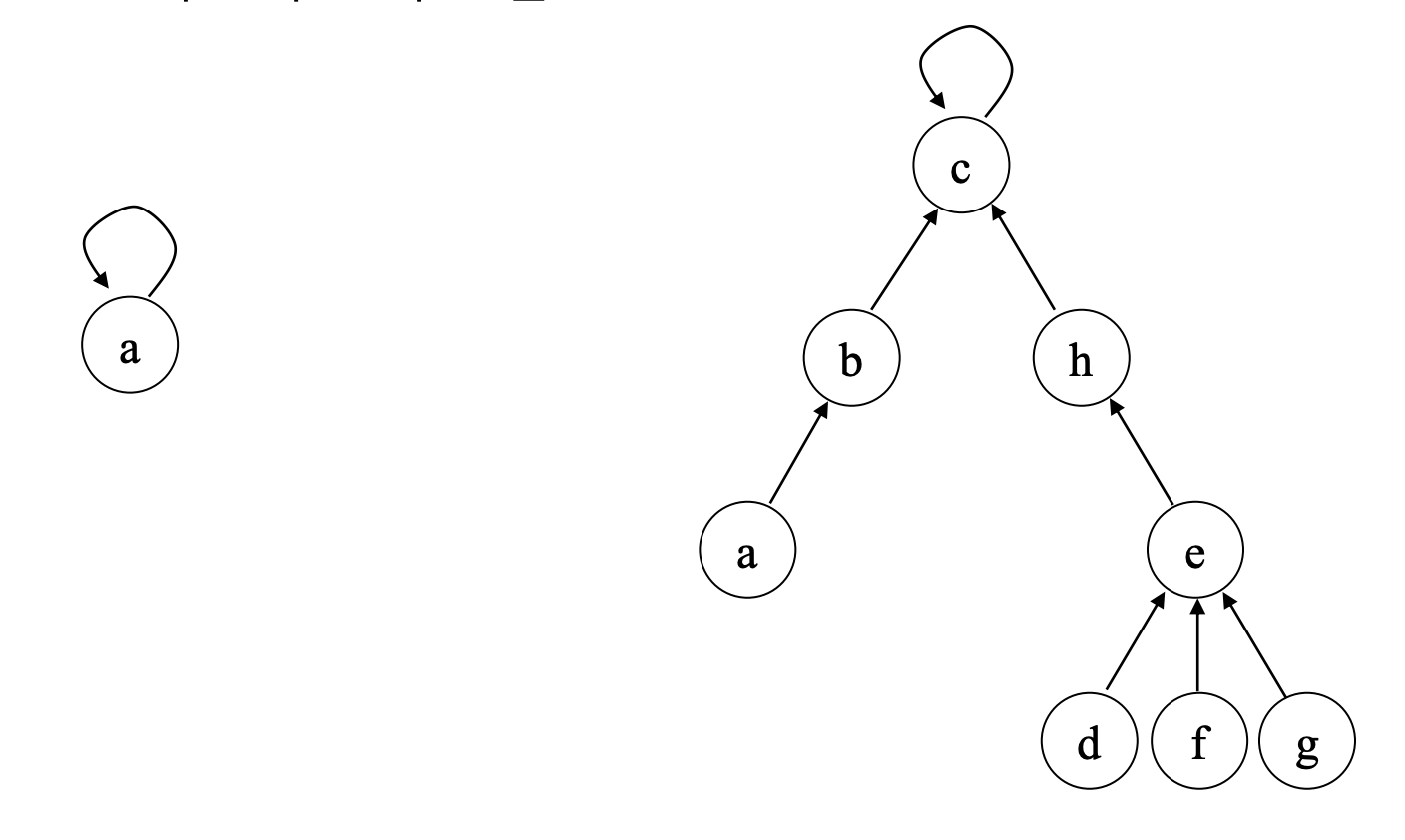
Union(x,y)를 보면 다음과 같다.
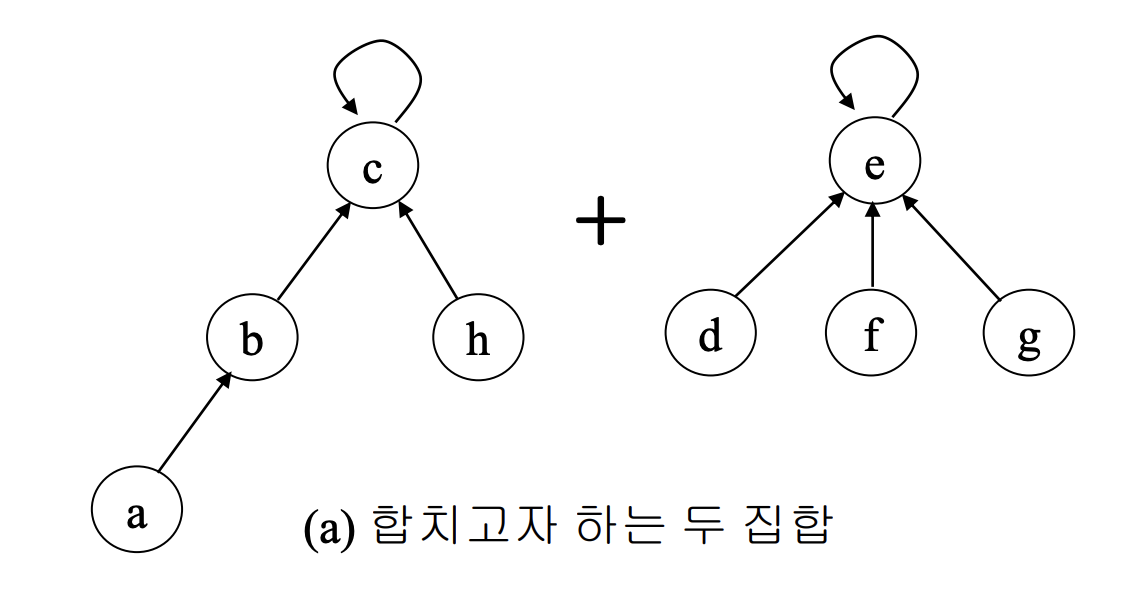
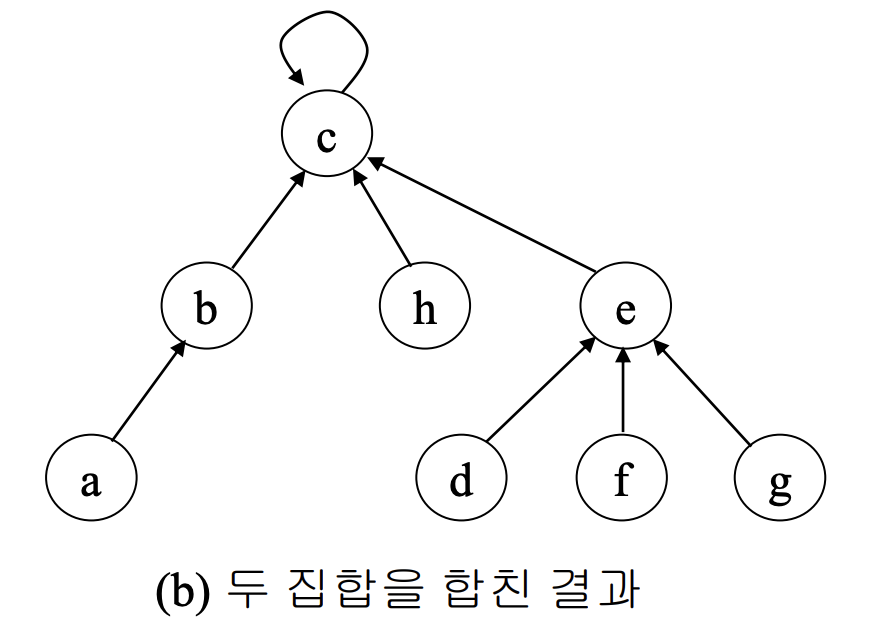
트리를 이용한 집한 연산의 기본 형태를 보면 다음과 같다.

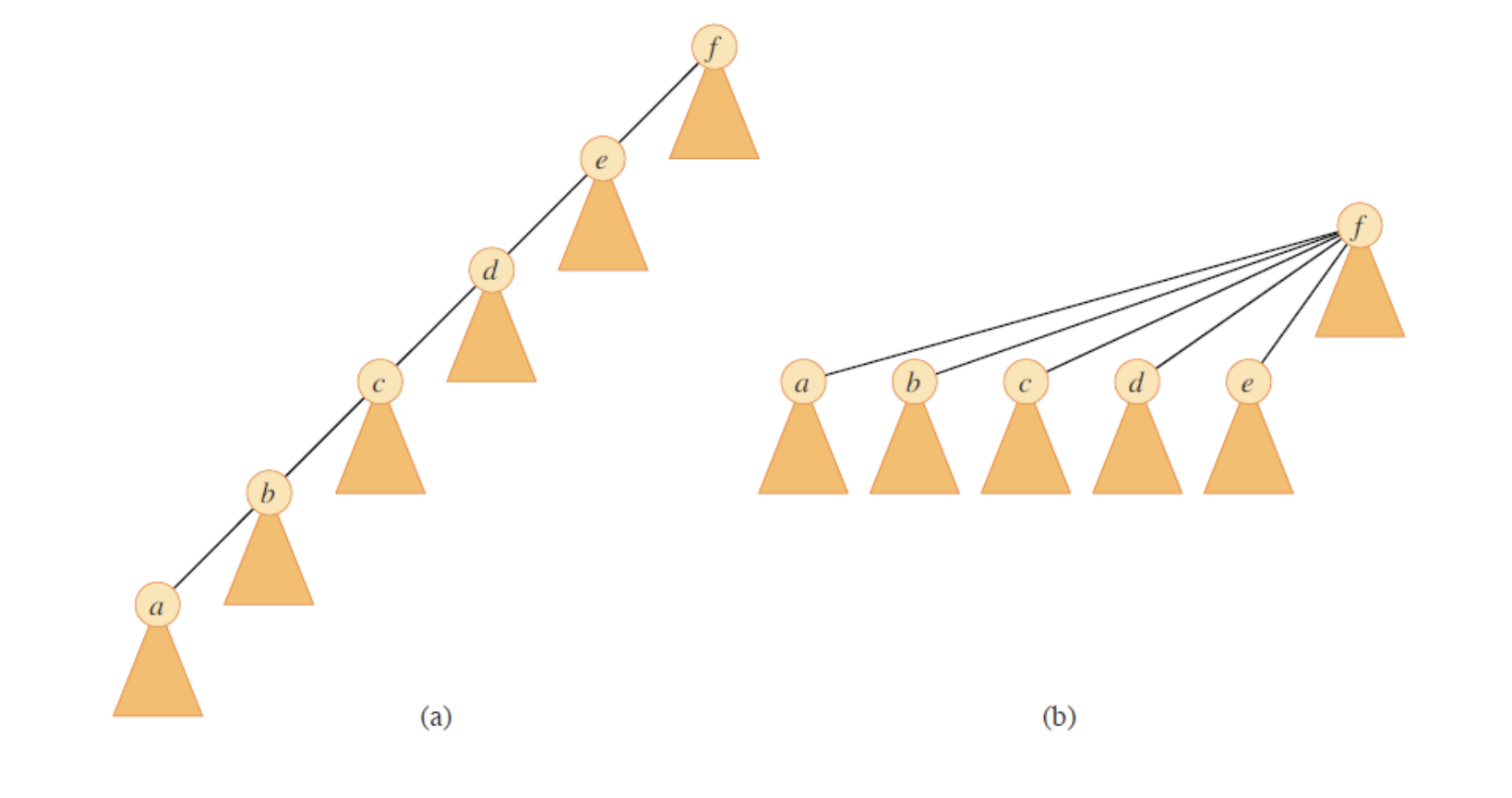
앞서 다룬 연산들만으로는 연결 리스트를 이용한 표현 방식과 비교하여 연산 효율 측면에서 더 나아지지 않는다. Union 과정을 통해서 마치 리스트와 같이 일렬로 연결된 트리가 나올 수도 있다.
연산 효율을 높이기 위한 방법
-랭크를 이용한 Union
▪ 각 노드는 자신을 루트로 하는 서브트리의 높이를 랭크(Rank)라는 이름으로 저장한다.
▪ 두 집합을 합칠 때 랭크가 낮은 집합을 랭크가 높은 집합에 붙인다.
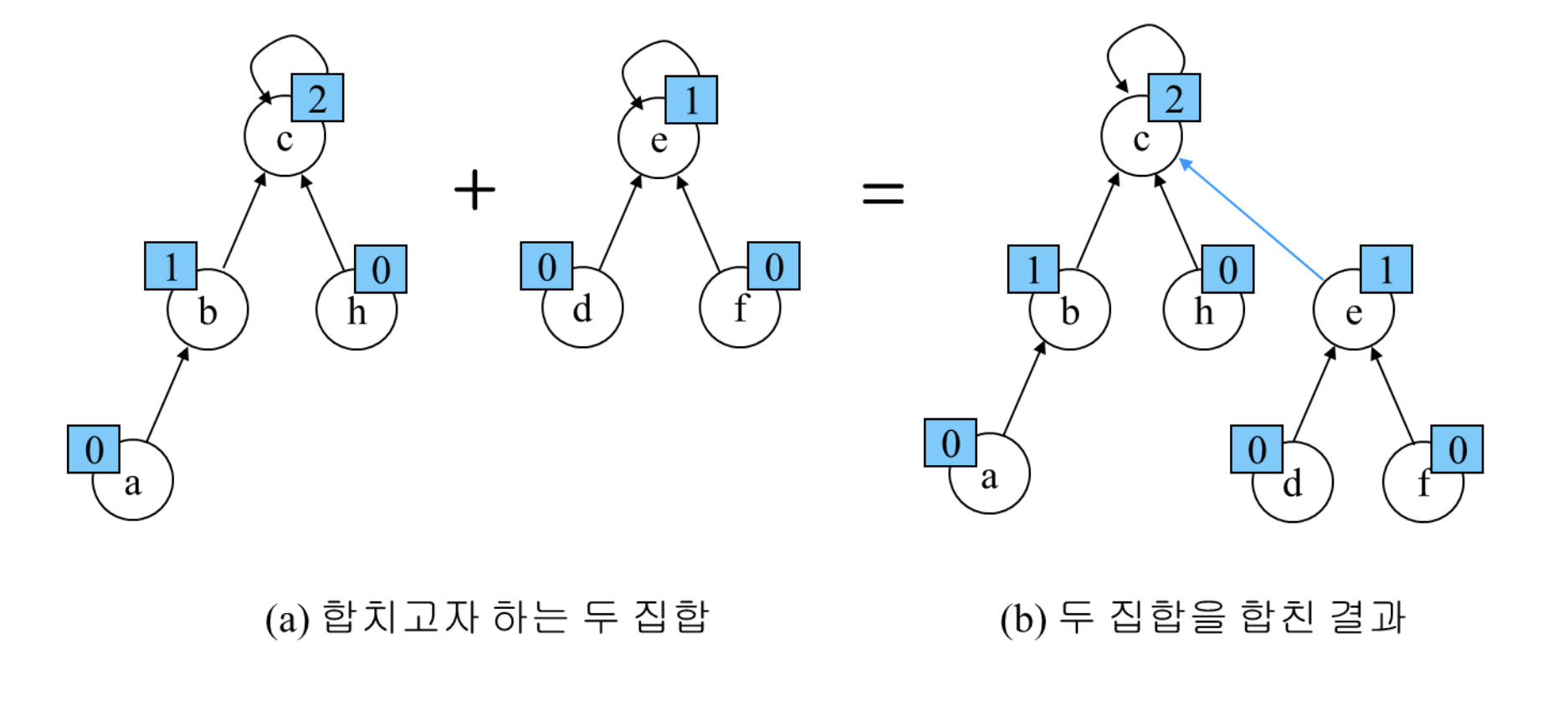
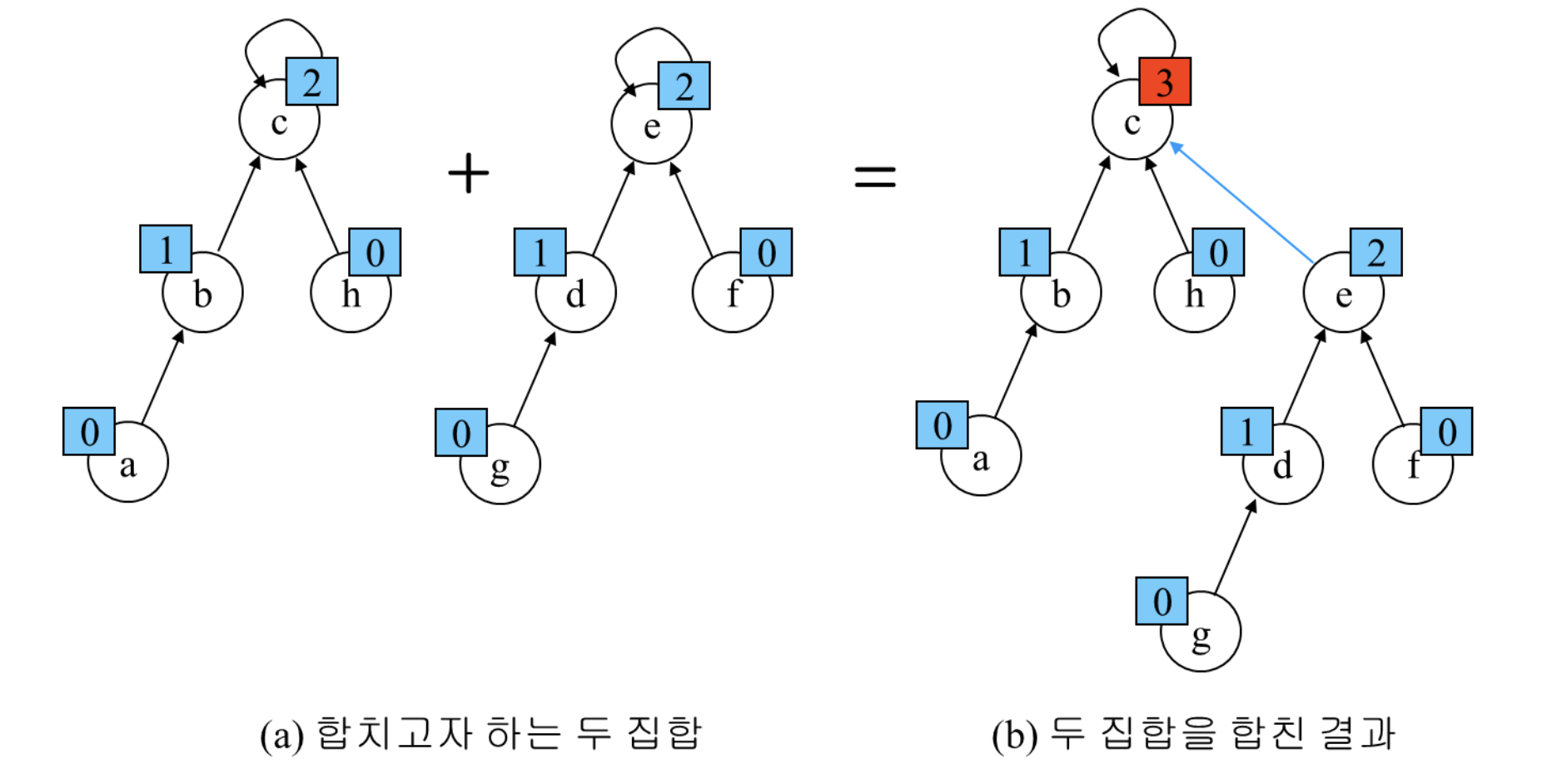
-경로압축
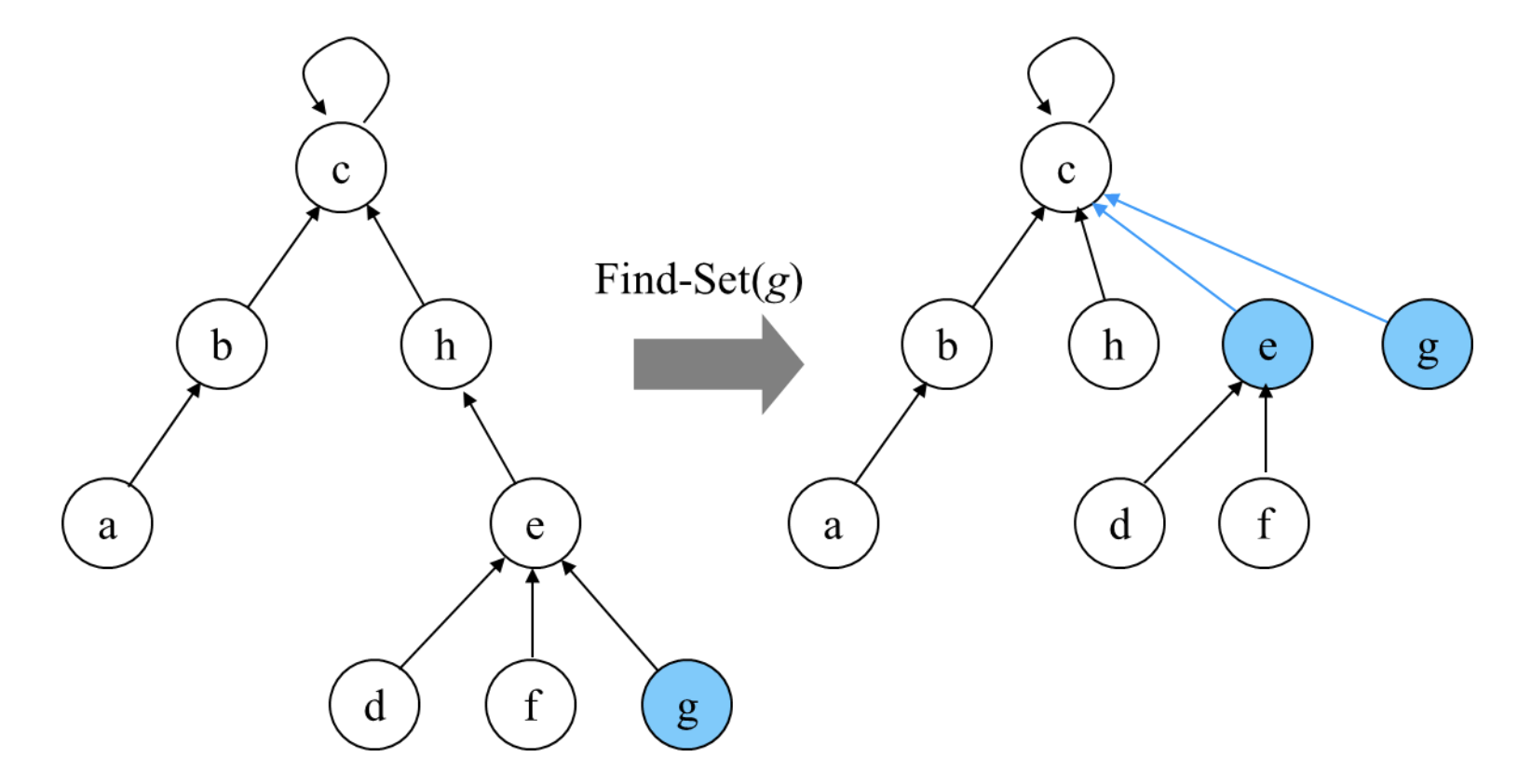
▪ Find-Set을 행하는 과정에서 만나는 모든 노드들이 직접 루트를 가리키도록 포인터를 바꾸어 준다.


'Univ. Study > Algorithm Design' 카테고리의 다른 글
| Lecture 17 - Graph(1/4) (0) | 2023.05.01 |
|---|---|
| Lecture 14 - Dynamic Programming (0) | 2023.04.24 |
| Lecture 11 - 해시 테이블 (0) | 2023.04.03 |
| Lecture5,6 - 정렬알고리즘(1) (1) | 2023.03.20 |
| Lecture4 - 점화식과 점근적 복잡도 분석 (0) | 2023.03.08 |



