점화식의 이해
점화식이란 어떤 함수(보통 입력 변수를 n등의 미지수로 표현)를 자신보다 더 작은 변수에 대한 함수와의 관계로 표현한 식이다.
병합 정렬 알고리즘을 통해 살펴보자
mergeSort(A[],p,r){
if(p<r) then {
q<-[(p+r)/2]; #p,q의 중간 지점 계산
mergSort(A,p,q); #전반부 정렬
mergSort(A,q+1,r); #후반부 정렬
merge(A,p,q,r); #병합
}
}
merge(A[],p,q,r){
정렬되어 있는 두 배열 A[p...q]와 A[q+1...r]을 합하여
정렬된 하나의 배열 A[p...r]을 만든다.
}첫줄의 mergeSort(A[],p,r)는 T(n)로 두고 전반부 정렬, 후반부정렬의 mergeSort()를 각각 T(n/2)로 두면 수행 시간의 점화식은 다은과 같다. T(n) = 2T(n/2) + 오버헤드
이때 오버헤드 부분은 병합 파트인 merge(A,p,q,r)라고 둘 수 있는데 이는 n/2~n 사이의 값으로 Θ(n)임을 알 수 있다.
따라서 시간 복잡도를 T(n) = 2T(n/2) + Θ(n)로 생각할 수 있다.
점화식의 점근적 분석 방법 종류
▪ 반복 대치
점화식을 더 작은 문제에 대한 함수로 반복해서 대치해나가며 분석하는 방법

Factorial 알고리즘 점화식: T(n) = T(n-1) + c

병합 정렬 점화식: T(n) ≤ 2T(n/2) + n
n=2^k로 두면 다음과 같다.

▪ 추정 후 증명
해당 점화식의 복잡도에 대해 추정한 후 수학적 귀납법으로 증명하는 방법
병합 정렬 점화식: T(n) ≤ 2T(n/2) + n
추정: T(n) = O(nlogn), 즉 T(n) ≤ cnlogn
증명: 경계조건 - 𝑇(2) ≤ 𝑐2log2를 만족하는 c가 존재한다 (귀납법에서의 basis step에 해당)
귀납적 가정 및 전개 - n/2에 대해 𝑇(𝑛/2) ≤ 𝑐(𝑛/2)log(𝑛/2)가 성립한다면 다음과 같이 증명이 가능하다.
간단히 말하면 결계조건 및 귀납적전개 둘다 만족하는 c가 필요하다는 것이다.
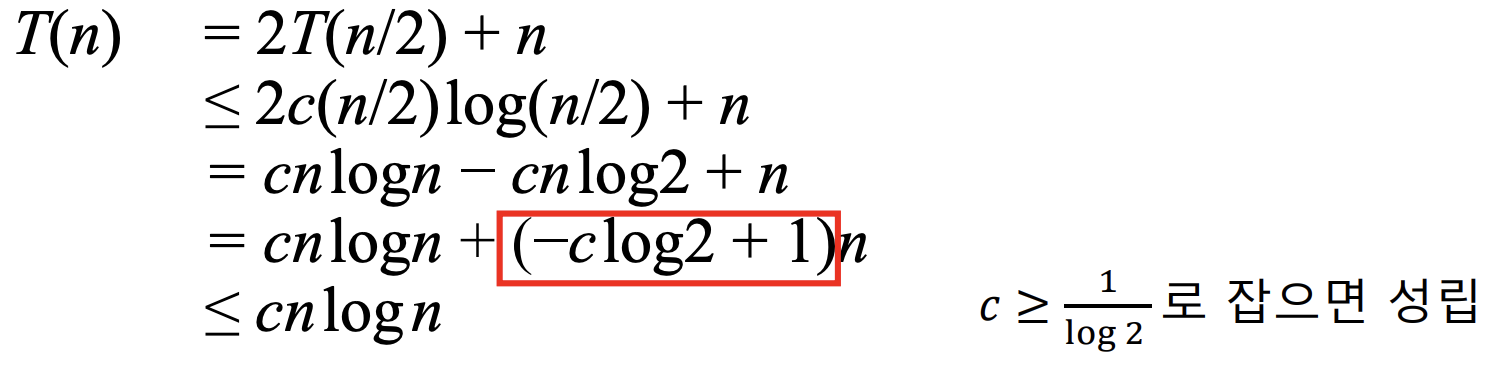
▪ 마스터 정리(Master Theorem)
점화식 형태에 따른 복잡도를 바로 계산할 수 있는 방법
아래와 같은 형식을 갖는 점화식의 점근적 복잡도는 마스터 정리에 의해 바로 결과 도출 가능하다.
T(n) = aT(n/b) + f(n)

위와 같이 h(n)을 가정하면 아래와 같은 세줄의 마스터 정리를 만족한다.

이런 정리는 조금 복잡한 감이 있어서 근사 버전과 직관적 의미를 살펴보자

직관적 의미는 다음과 같다.
- h(n)이 더 무거우면 h(n)이 수행 시간을 결정한다.
- f(n)이 더 무거우면 f(n)이 수행 시간을 결정한다.
- h(n)과 f(n)이 같은 무게이면 h(n)에 logn을 곱한 것이 수행 시간이 된다.
'Univ. Study > Algorithm Design' 카테고리의 다른 글
| Lecture 13 - 집합의 처리 (0) | 2023.04.10 |
|---|---|
| Lecture 11 - 해시 테이블 (0) | 2023.04.03 |
| Lecture5,6 - 정렬알고리즘(1) (1) | 2023.03.20 |
| Lecture3 - 알고리즘 설계와 분석의 기초(2) (1) | 2023.03.06 |
| Lecture1,2 - 알고리즘 설계와 분석의 기초(1) (0) | 2023.03.05 |



