728x90
Support Vector Regression
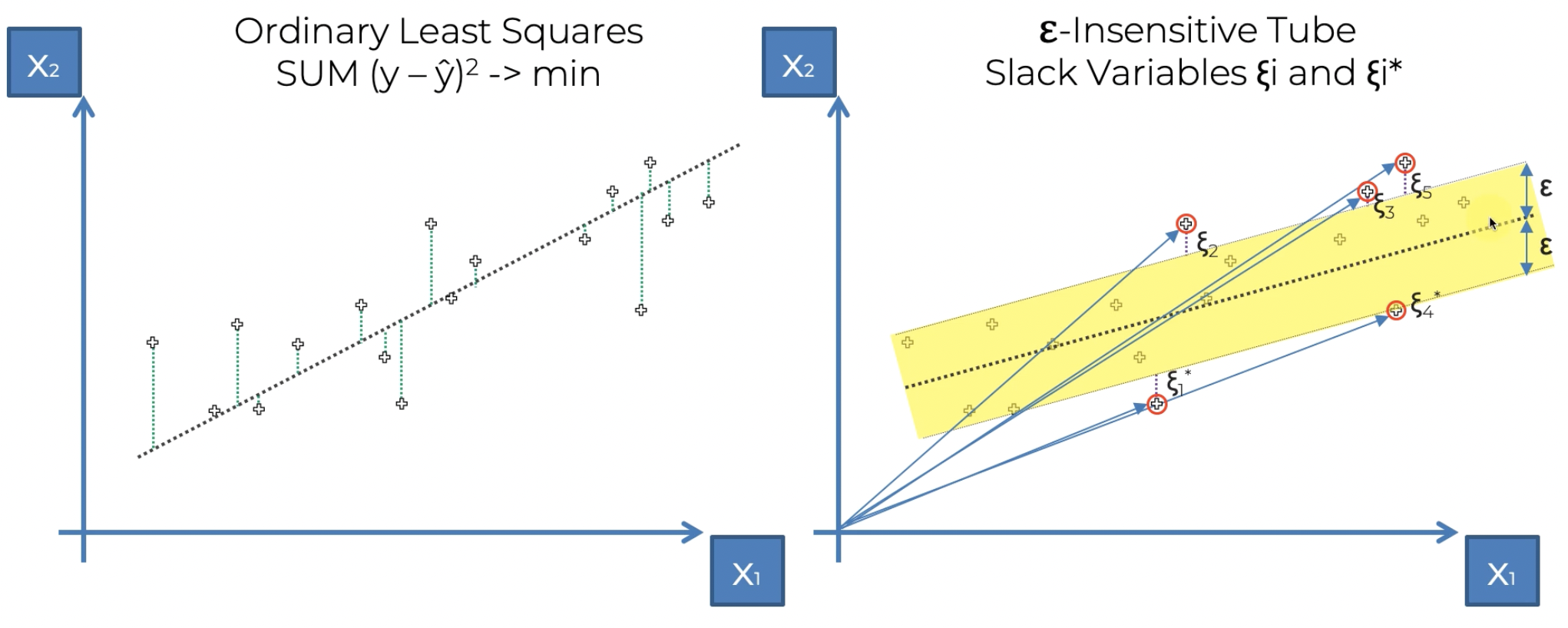
기존의 최소 제곱법은 회귀선을 그리고 점과 회귀선 사이의 거리의 제곱의 합을 최소화하는 방법을 통해 적절한 회귀선을 찾았다면
SVR에서는 ε-Insensitive Tube를 이용한다. 이 튜브는 이름 그대로 튜브 내부의 점들의 오차는 무시한다. 튜브의 세로 길이가 중요하다. 이는 중심선에 수직이 아니라 x1축에 수직으로 측정한다. 모형에 일정 수준의 오차 허용 범위를 제공하는 것이다.
중요한 것은 튜브 외부의 점들이다. 해당 점들의 오차는 튜브중심이 아닌 튜브 그 자체까지의 거리를 통해 연산한다.
Support Vector Regression이란 이름도 vector로 표현되는 오차점들이 튜브의 구조를 형성한다고 해서 붙혀진 이름이다.
계산 식은 다음과 같다.
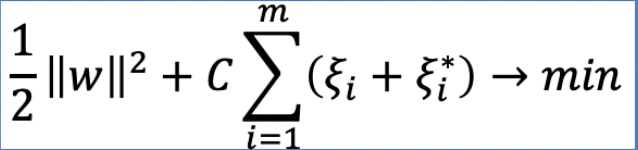
SVR model
이번 모델은 이전의 모델들에 비해서는 조금 난이도가 있는 편이다. 이는 feature scaling과정이 복잡하기 때문이다.
#Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
#Importing the dataset
dataset = pd.read_csv('Position_Salaries.csv')
X = dataset.iloc[:, 1:-1].values
y = dataset.iloc[:, -1].values
print(X)
[[ 1]
[ 2]
[ 3]
[ 4]
[ 5]
[ 6]
[ 7]
[ 8]
[ 9]
[10]]
print(y)
[ 45000 50000 60000 80000 110000 150000 200000 300000 500000
1000000]
#세로로 데이터를 정렬(feature scaling input형태는 정해져있기 때문)
y = y.reshape(len(y),1)
print(y)
[[ 45000]
[ 50000]
[ 60000]
[ 80000]
[ 110000]
[ 150000]
[ 200000]
[ 300000]
[ 500000]
[1000000]]
#Feature Scaling
from sklearn.preprocessing import StandardScaler #feature scaling 클래스
#이전에 feature scaling을 배울때와는 다르게 종속 변수 y에도 feature scaling 적용
sc_X = StandardScaler()
sc_y = StandardScaler() #y값이 45000에서 1000000까지 너무 폭이 크기 때문에 feature scaling적용
X = sc_X.fit_transform(X)
y = sc_y.fit_transform(y)
print(X)
[[-1.5666989 ]
[-1.21854359]
[-0.87038828]
[-0.52223297]
[-0.17407766]
[ 0.17407766]
[ 0.52223297]
[ 0.87038828]
[ 1.21854359]
[ 1.5666989 ]]
print(y)
[[-0.72004253]
[-0.70243757]
[-0.66722767]
[-0.59680786]
[-0.49117815]
[-0.35033854]
[-0.17428902]
[ 0.17781001]
[ 0.88200808]
[ 2.64250325]]
#Training the SVR model on the whole dataset
from sklearn.svm import SVR #SVR클래스 import
regressor = SVR(kernel = 'rbf') #Gaussian RBF Kernel
regressor.fit(X, y)
#Predicting a new result
#직접 6.5를 넣을 수 없고 transform 과정을 거쳐야하고 나온 결과도 inverse_transform 과정을 통해
#우리가 원하는 범위의 값으로 출력을 해야 결과를 적절하게 가져올 수 있음
sc_y.inverse_transform(regressor.predict(sc_X.transform([[6.5]])).reshape(-1,1))
array([[170370.0204065]])위에서 사용된 Gaussian RBF Kernel은 다음과 같은 식으로 표현된다.
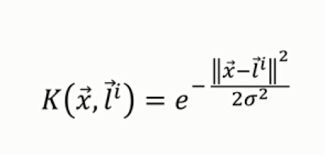
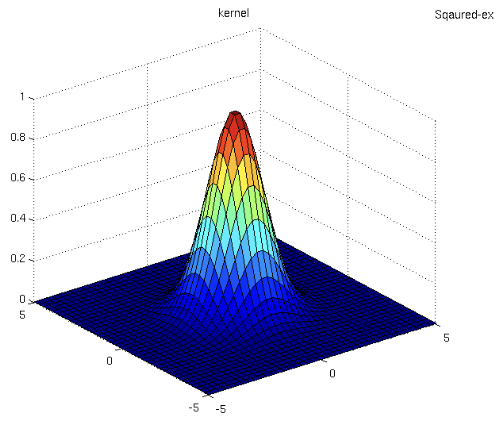
그리고 rbf 방사형 커널을 그래프로 보면 다음과 같다.
#Visualising the SVR results
plt.scatter(sc_X.inverse_transform(X), sc_y.inverse_transform(y), color = 'red')
plt.plot(sc_X.inverse_transform(X), sc_y.inverse_transform(regressor.predict(X).reshape(-1,1)), color = 'blue')
plt.title('Truth or Bluff (SVR)')
plt.xlabel('Position level')
plt.ylabel('Salary')
plt.show()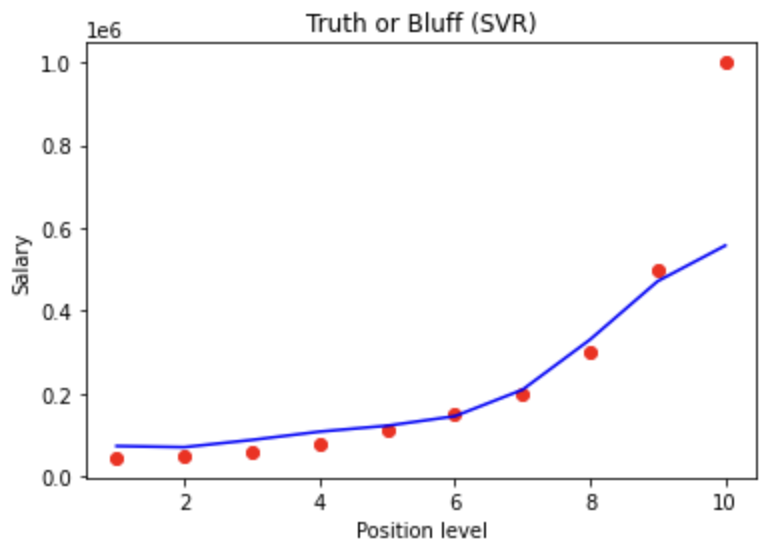
#Visualising the SVR results (for higher resolution and smoother curve)
X_grid = np.arange(min(sc_X.inverse_transform(X)), max(sc_X.inverse_transform(X)), 0.1)
X_grid = X_grid.reshape((len(X_grid), 1))
plt.scatter(sc_X.inverse_transform(X), sc_y.inverse_transform(y), color = 'red')
plt.plot(X_grid, sc_y.inverse_transform(regressor.predict(sc_X.transform(X_grid)).reshape(-1,1)), color = 'blue')
plt.title('Truth or Bluff (SVR)')
plt.xlabel('Position level')
plt.ylabel('Salary')
plt.show()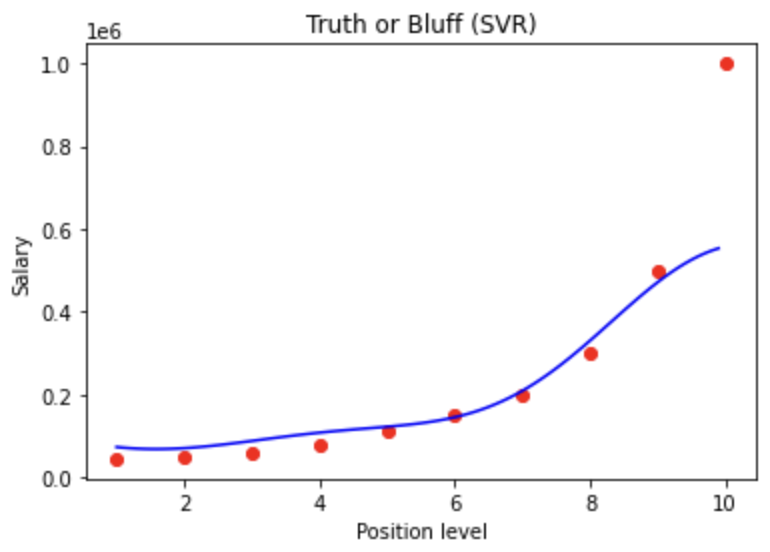
Feature scaling되어 있는 독립변수와 종속변수를 다루기 때문에 transform, inverse_transform 과정을 적절하게 다뤄야 원하는 데이터 값을 얻는것에 문제가 없다.
728x90
'Drawing (AI) > MachineLearning' 카테고리의 다른 글
| Udemy - 머신러닝의 모든 것 (Random Forest Regression) (0) | 2023.03.18 |
|---|---|
| Udemy - 머신러닝의 모든 것 (Decision Tree) (0) | 2023.03.17 |
| Udemy - 머신러닝의 모든 것 (Polynomial Linear Regression) (0) | 2023.03.11 |
| Udemy - 머신러닝의 모든 것 (Multiple Linear Regression-2) (0) | 2023.02.28 |
| AI스터디자료-1주차 (0) | 2023.02.11 |



