CART
CART는 Classification Trees와 Regression Trees를 모두 포함한 개념이다. 회귀를 공부하고 있었던 만큼 이번에는 Regression Tree에 집중해서 공부해보고자 한다.
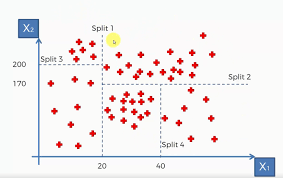
위와 같이 데이터들을 어떤 기준에 따라 나누어 가다가 정보 엔트로피라는 복잡한 수학적 개념에 따라 알고리즘이 split을 멈춰야할 때를 파악하고 정보추가를 멈춘다. 이 잎(위와 같은 데이터를 leaf라고 부름)들을 가르는 기준선의 수에 따라 알고리즘에 정보를 더 넣을 수도 있고 넣는 걸 멈출 수도 있다.

4가지 split을 통해 구성된 알고리즘이다. x1 < 20이 기준인 split1 이후에 20보다 큰 값들을 x2 < 170이 기준인 split2로 또 나누고 20보다 작은 값들은 x3 < 200이 기준인 split3로 나눈다. split2를 통해 x2 < 170인 경우를 x1 < 40인 split4를 기준으로 나누어서 결과값을 어떤식으로 예측할지 결정한다.
의사 결정 트리 회귀
의사 결정 트리 회귀에서는 feature scaling 과정을 고민할 필요가 없다. 왜냐하면 위의 이론에서 공부했듯이 data들을 split하는 과정을 통해 학습이 진행되기 때문이다. 나누기만 하면되기 때문에 data들의 범주가 어떻냐는 중요하지 않게 되는 것이다.

#Decision Tree Regression
#Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
#Importing the dataset
dataset = pd.read_csv('Position_Salaries.csv')
X = dataset.iloc[:, 1:-1].values
y = dataset.iloc[:, -1].values
#Training the Decision Tree Regression model on the whole dataset
from sklearn.tree import DecisionTreeRegressor
regressor = DecisionTreeRegressor(random_state = 0)
regressor.fit(X, y)
#Predicting a new result
regressor.predict([[6.5]])
array([150000.])다음은 시각화 파트인데 이전 회귀들과 달리 higher resolution 결과만 확인한다.
왜냐하면 기본적으로 의사 결정 트리 회귀 방식은 우리가 지금 다루는 데이터와 같은 단독 요소 데이터에 적합하지 않고 여러 요소들이 있는 고차원 데이터 집합에 적합하기 때문이다.
X_grid = np.arange(min(X), max(X), 0.01)
X_grid = X_grid.reshape((len(X_grid), 1))
plt.scatter(X, y, color = 'red')
plt.plot(X_grid, regressor.predict(X_grid), color = 'blue')
plt.title('Truth or Bluff (Decision Tree Regression)')
plt.xlabel('Position level')
plt.ylabel('Salary')
plt.show()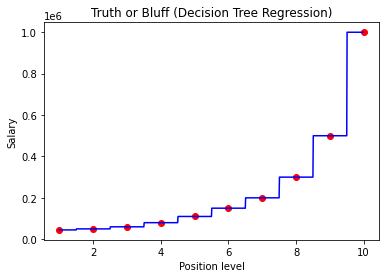
시각화된 예측 그래프를 보면 의사 결정 트리 회귀가 어떤식으로 학습을 하는지 잘 볼 수 있다. 정보가 주어져 있는 직급주변을 공평하게 나눠서 해당 boundary까지는 일정한 salary를 지정하였기에 계단형으로 상승한다.
'Robotics & AI > MachineLearning' 카테고리의 다른 글
| Udemy - 머신러닝의 모든 것 (회귀 모델 성능 평가) (0) | 2023.03.20 |
|---|---|
| Udemy - 머신러닝의 모든 것 (Random Forest Regression) (0) | 2023.03.18 |
| Udemy - 머신러닝의 모든 것 (SVR) (0) | 2023.03.12 |
| Udemy - 머신러닝의 모든 것 (Polynomial Linear Regression) (0) | 2023.03.11 |
| Udemy - 머신러닝의 모든 것 (Multiple Linear Regression-2) (0) | 2023.02.28 |



