다항식 회귀
아래와 같이 polynomial linear regression은 multiple linear regression과 유사하다. 그러나 polynomial linear regression은 다양한 x1, x2, ... xn 변수들이 존재하는 multiple linear regression과는 달리 같은 x1변수에 대해 n제곱 꼴로 이루어져 있음을 알 수 있다.

아래와 같은 방식으로 데이터가 분포해 있을 경우 단순 선형 회귀 방식으로는 적절한 모델을 만들 수 없다. 데이터의 분포의 경향성이 곡선에 가깝기 때문이다.

Why Linear?
Polynomial Linear Regression은 polynomial함에도 linear이라는 이름이 붙어있다. 이는 굉장히 이상하게 느껴질 수 있다.
여기서 문제는 linear 즉 선형적이라는 말은 x변수끼리나 x,y변수간의 관계에 의해 결정되지 않는다는 것이다.
핵심은 coefficient 즉 계수이다. 아무리 x변수가 polynomial해도 궁극적으로 우리가 찾고자하는 것은 모델의 가중치, 즉 계수이기 때문에 계수가 선형적으로 결합할 수 있다면 해당 모델은 선형적이라고 볼 수 있는 것이다.
추가적으로 다항식회귀는 새로운 회귀라기 보다는 다중회귀중 한가지 타입이라고 볼 수 있다.
Polynomial Linear Regression Model
처음으로 비선형적인 경향성이 있는 데이터에 대한 모델을 만들어보고자 한다.
어떤 사람을 채용하는데 그 사람이 본인은 연봉으로 $160000를 받고자 하는데 그 이유가 이전 회사에서 해당 수준의 급여를 받았기 때문이라고 주장한다. 이때 고용자 입장에서 적절한 급여 수준으로 협상을 진행하기 위해 그 사람에 대한 정보와 그 사람이 다니던 회사의 급여 구조에 대한 정보를 토대로 그 사람의 주장이 맞는지 확인하고자 한다. 따라서 그 사람에 대한 정보만 입력하면 그 사람의 기대 급여 수준이 어느정도인지 예측할 수 있는 모델을 만들고자 한다.

위 데이터는 그 사람이 다니던 회사의 급여 체계이다.
#Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
#Importing the dataset
dataset = pd.read_csv('Position_Salaries.csv')
X = dataset.iloc[:, 1:-1].values #첫번째 열 제외
y = dataset.iloc[:, -1].values
#Training the Linear Regression model on the whole dataset
from sklearn.linear_model import LinearRegression #선형회귀 클래스
lin_reg = LinearRegression()
lin_reg.fit(X, y) #데이터에 적합하게 학습
#Training the Polynomial Regression model on the whole dataset
from sklearn.preprocessing import PolynomialFeatures #다항 클래스
poly_reg = PolynomialFeatures(degree = 4) #요소 행렬을 만들때 최고차항 결정
X_poly = poly_reg.fit_transform(X) #요소 행렬과 선형회귀를 합쳐 다항회귀
lin_reg_2 = LinearRegression()
lin_reg_2.fit(X_poly, y)이번 모델의 특징이라면 학습을 시킬 때 training set과 test set으로 나누지 않는다는 것이다. 이는 데이터의 수가 부족하기 때문에 전체로 training을 진행하지 않으면 좋은 모델 만들 수 없기 때문이다.
단순 선형 회귀와 다항 회귀를 비교하기 위해 시각화 과정을 거치고자 한다.
#Visualising the Linear Regression results
plt.scatter(X, y, color = 'red') #그래프에 표현할 실제 데이터의 좌표와 점의 색 설정
plt.plot(X, lin_reg.predict(X), color = 'blue') #회귀선 표현
plt.title('Truth or Bluff (Linear Regression)')
plt.xlabel('Position Level')
plt.ylabel('Salary')
plt.show()
단순 선형 회귀로 모델을 만들자 데이터와의 오차가 큰 것을 확인할 수 있다. 데이터 자체가 비선형적이기 때문이다.
#Visualising the Polynomial Regression results
plt.scatter(X, y, color = 'red') #그래프에 표현할 실제 데이터의 좌표와 점의 색 설정
plt.plot(X, lin_reg_2.predict(poly_reg.fit_transform(X)), color = 'blue') #회귀선 표현
plt.title('Truth or Bluff (Polynomial Regression)')
plt.xlabel('Position level')
plt.ylabel('Salary')
plt.show()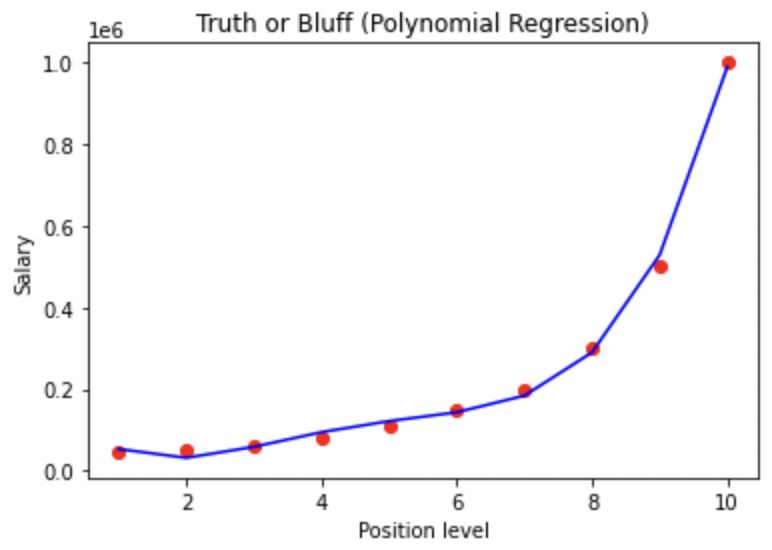
다항 회귀로 분석하자 훨씬 더 적절한 모델이 완성된 것을 볼 수 있다.
#Visualising the Polynomial Regression results (for higher resolution and smoother curve)
X_grid = np.arange(min(X), max(X), 0.1)
X_grid = X_grid.reshape((len(X_grid), 1))
plt.scatter(X, y, color = 'red')
plt.plot(X_grid, lin_reg_2.predict(poly_reg.fit_transform(X_grid)), color = 'blue')
plt.title('Truth or Bluff (Polynomial Regression)')
plt.xlabel('Position level')
plt.ylabel('Salary')
plt.show()
더 높은 해상도와 부드러운 커브를 가진 그래프이다.
#Predicting a new result with Linear Regression
lin_reg.predict([[6.5]]) #예측은 배열형태로 입력해야함(여기선 2차원 배열)
#예측 결과
array([330378.78787879])
#Predicting a new result with Polynomial Regression
lin_reg_2.predict(poly_reg.fit_transform([[6.5]])) #예측은 배열형태로 입력해야함(여기선 2차원 배열)
#예측 결과
array([158862.45265155])단순 선형 회귀 모델과 다항 회귀 모델의 예측 결과를 보면 다항 회귀 모델이 훨씬더 적합한 결과를 냈고 입사자의 주장이 적절했음을 알 수 있다.
'Robotics & AI > MachineLearning' 카테고리의 다른 글
| Udemy - 머신러닝의 모든 것 (Decision Tree) (0) | 2023.03.17 |
|---|---|
| Udemy - 머신러닝의 모든 것 (SVR) (0) | 2023.03.12 |
| Udemy - 머신러닝의 모든 것 (Multiple Linear Regression-2) (0) | 2023.02.28 |
| AI스터디자료-1주차 (0) | 2023.02.11 |
| Udemy - 머신러닝의 모든 것 (Multiple Linear Regression-1) (0) | 2023.02.03 |



