728x90
Scalar vs Vector
Scalar: 크기만 존재하는 물리량 ex) temperature, time, ditance, mass, density, pressure, voltage...
Vector: 크기와 방향이 모두 존재하는 물리량 ex) force, velocity, acceleration
Scalar field: 스칼라장(스칼라 물리량의 위치별 분포)
Vector field: 벡터장(벡터 물리량의 위치별 분포)


Vector

벡터는 위와 같이 시점, 종점, 길이로 표현이된다.
벡터간의 연산은 다음과 같다.



벡터 연산도 결합법칙과 교환법칙이 성립된다.
Vector Representation using Orthogonal Rectangular Unit Vectors
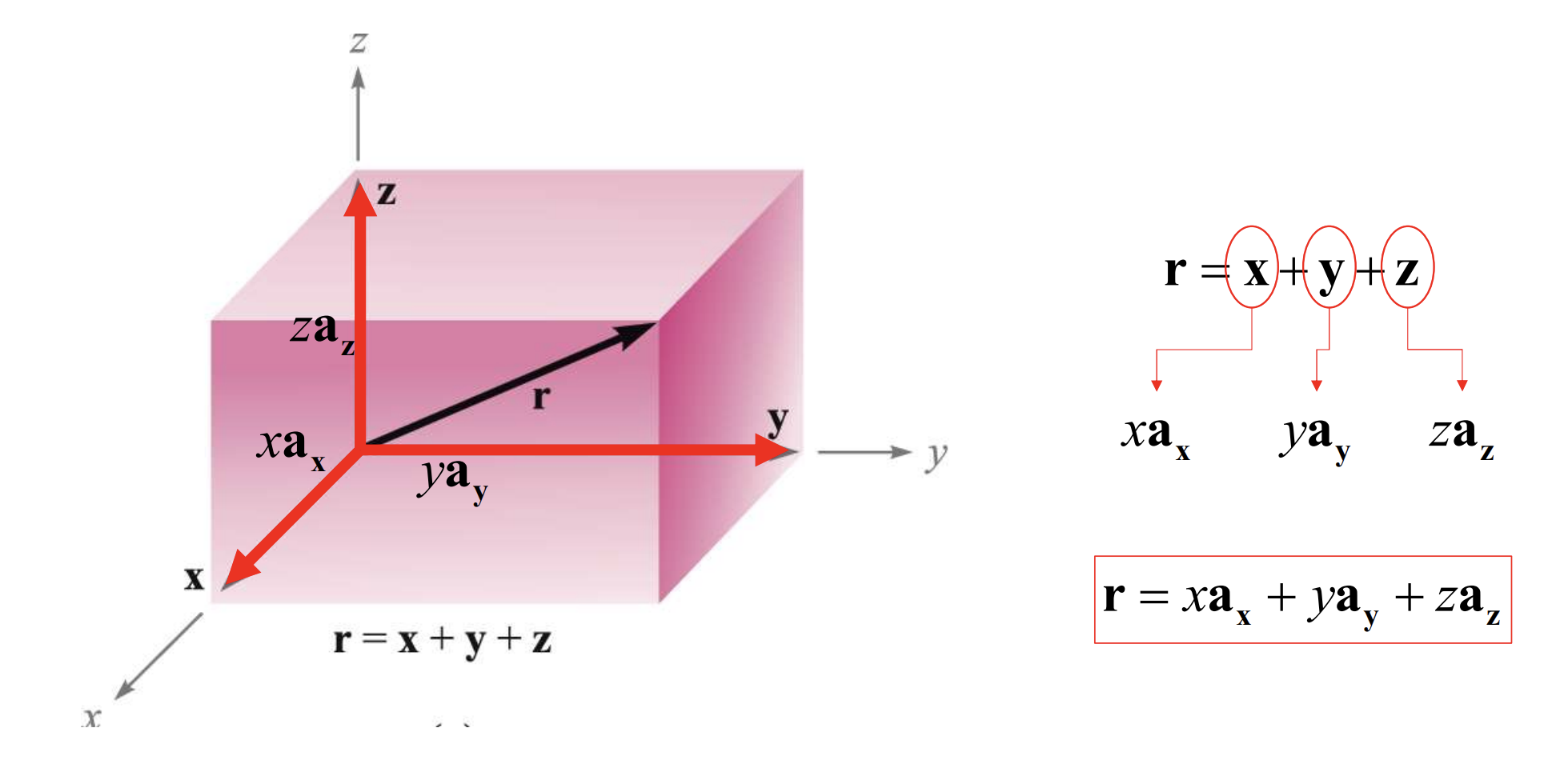
위의 방식처럼 벡터를 표현하면 다음과 같이 벡터의 연산도 진행할 수 있다.

직교 좌표에서의 다양한 벡터 표현
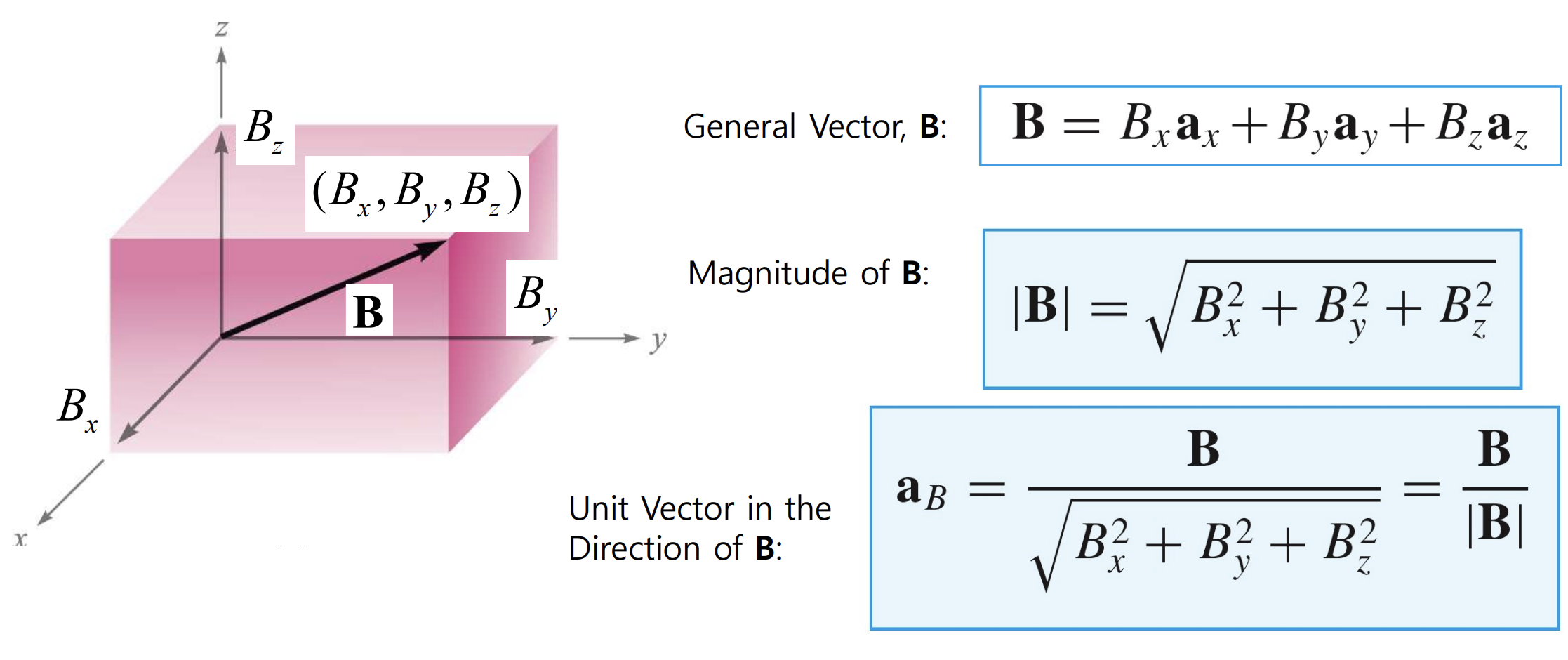
벡터장
벡터장은 다음과 같이 각각의 벡터성분의 계수가 성분들에 대한 식으로 표현이 된다.
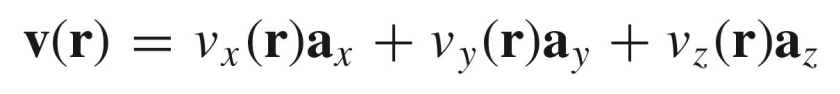
예시 문제를 통해 벡터장에 대한 이해를 해보자.
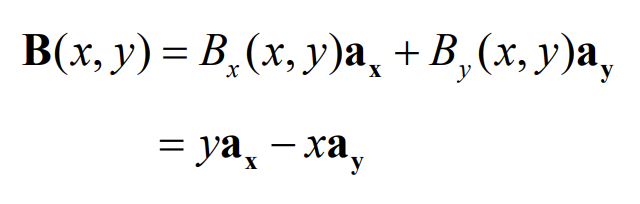
위의 식으로 표현된 벡터장을 그림으로 그리면 다음과 같다.
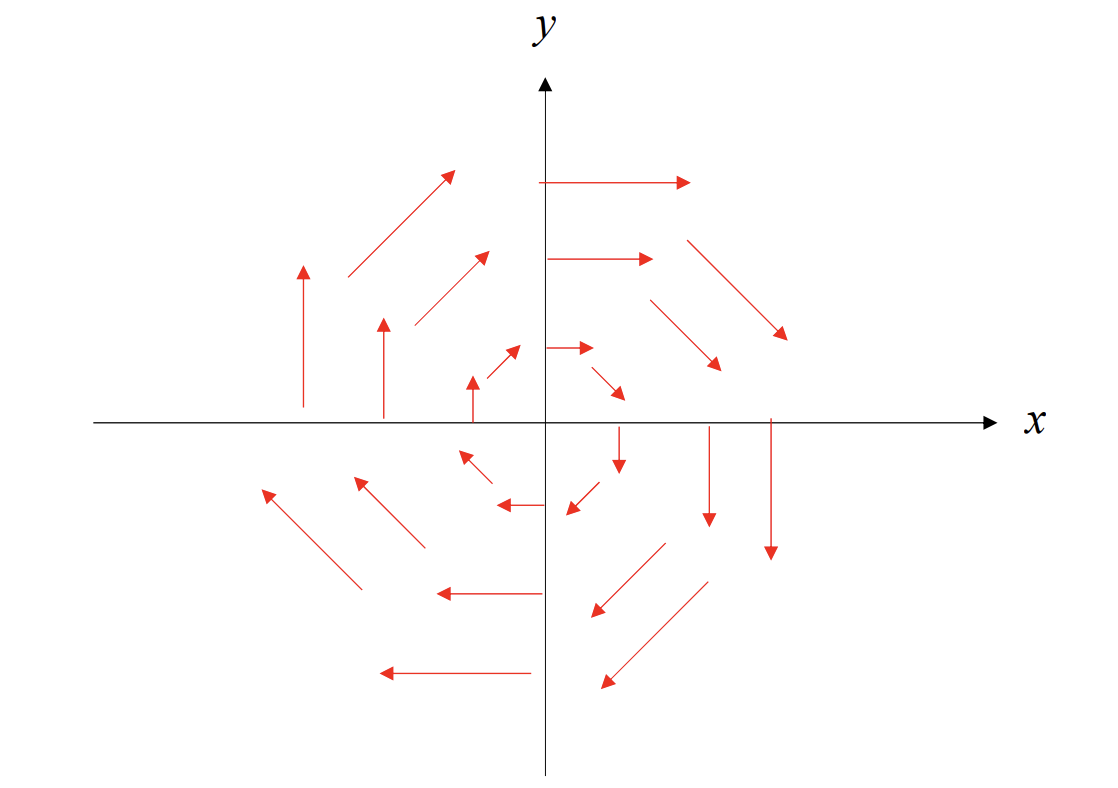
아직 직관적으로 떠올리기에는 어려움이 있어서 좌표에 해당하는 벡터를 하나하나 그려가며 경향성을 파악해서 완성할 수 있었다.
Dot product
내적은 Dot Product, Scalar Product, Inner Product라는 다양한 이름으로 불리었다.
연산 방법은 다음과 같다.

위의 연산을 활용하면 벡터간의 연산을 계수들만으로 해결하는 방법도 알 수 있다.
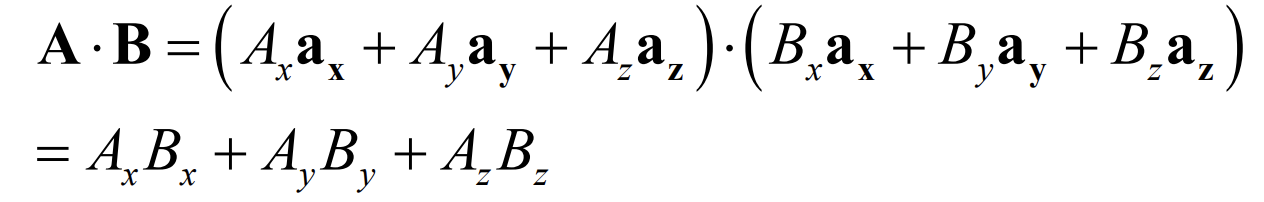
728x90
'Quality control (Univ. Study) > Electromagnetics' 카테고리의 다른 글
| Lecture7 - Electric Field(2) (0) | 2023.04.08 |
|---|---|
| Lecture6 - Electric Field (0) | 2023.03.30 |
| Lecture5 - Columb's Law (0) | 2023.03.30 |
| Lecture4-Vector Analysis(3) (0) | 2023.03.21 |
| Lecture3-Vector Analysis(2) (0) | 2023.03.09 |



