The Neuron
인공신경망(Artificial Neural Network, 이후 ANN)을 구현하기 위해 제일 먼저 이해해야하는 것은 Neuron이다.

뉴런 한개는 아무런 일도 할 수 없지만 이런 뉴런들이 군집을 만들어서 대단한 작업을 할 수 있게 된다.
협업을 하기 위해 가지돌기와 축삭돌기가 큰 역할을 한다. 가지돌기가 신호 수신기 역할을 하고 축삭돌기가 신호 발신기 역할을 한다. 축삭돌기에서 가지돌기로 신호가 전달되는 부분에는 작은 틈이 존재하는데 그것을 시냅스라고 부른다.
이제 이런 뉴런을 기술적으로 구현하고자한다.

Input의 value는 표준화를 통해 일정한 범위의 값들을 function에 넣어준다. 이때 표준화란 평균을 0으로 분산을 1로 하는 방식이고 normalization이라는 일정한 범위의 값으로 확장하는 방식도 있다.
각 Input에 가중치를 의미하는 weights를 적용해주고 함수에 값을 전달하는 시냅스가 있다. 가중치를 결정하는 과정에서 다른 수업에서 들었던 Gradient descent와 같은 내용이 적용된다. 각 신호들을 더하고 activation fuction을 통해 output에 전달 한다.
Activate fuction
활성화 함수는 다양한 종류가 있지만 그중 대표적인 4가지 활성화 함수를 알아보자

우선 Threshold function은 활성화 함수계의 yes or no이다. 0보다 작으면 무조건 0이되고 0보다크면 1이된다.
Threshold라는 말 그대로 한계점을 넘으면 값이 출력되도록 하는 활성화함수이다.
이는 선형대수학에서 공부한 u(t)함수와 같았다.

다음으로 Sigmoid function은 매끄럽고 점진적으로 변화하는 함수로 0보다 크면 1에 점진적으로 가까워지고 0보다 작으면 0에 점진적으로 가까워진다. 확률을 예측할때 유용하게 이용된다.
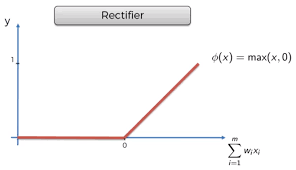
세번째는 Rectifier function이다. 이는 ANN에서 가장 많이 사용하는 활성화 함수중 하나로 한계치 0 이하일때는 0으로 값을 출력하지 않고 0이상이면 값이 증가된다.

마지막으로 Hyperbolic fuunction이다. 이는 한계치 0 을 기준으로 더 작을 때는 0이하로 내려가서 -1에 가까워지고 0이상일때는 1에 가까워진다.
How do Neural Networks work?
Neural Network(이후 NN)의 예시를 살펴볼 것인데 우선은 이미 훈련된 Neural Network을 이용한다고 본다.

위와 같이 hidden layer 없이 가중치만 이용해도 가격을 예측하는 것이 가능하지만
Hidden Layer가 추가되면서 NN은 그 정확도와 능력치가 엄청나게 증가한다.
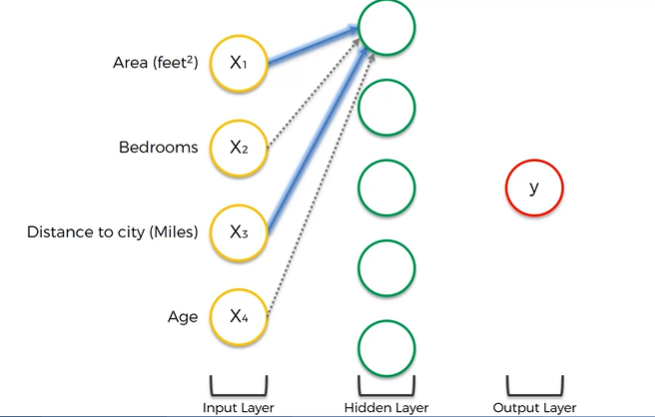
보통은 도시에서 멀어질 수록 같은 가격으로 더 넓은 부지의 부동산을 찾을 수 있다.
이를 통해 추측하건데 해당 뉴런은 도시에서 별로 멀지 않은 거리에 넓은 부지의 부동산이라는 특별한 경우를 찾는 뉴런이라고 볼 수 있다. 이때 침실 수와 연식같은 요인은 전혀 신경을 쓰지 않는다.
이런식으로 hidden layer의 뉴런들은 새로운 보다 구체적인 가치를 갖고 있는 환경변수 역할을 하게된다.

Hidden layer의 세번째 뉴런과 가장 아래 뉴런을 보자.
세번째 뉴런은 현대 가족들이 충분히 넓고 자식들에게 하나씩의 침실을 제공하기 위해 4개이상의 침실을 요구하고 오래되지 않은 집을 원하는 현상을 표현한다고 추측해 볼 수 있다.
반면에 마지막 뉴런은 Age input하나만 받는다. 이 뉴런은 특별한 역할을 할 수 있다. 예를들어 100년 이상된 고풍스런 귀족 가옥의 가치를 알아보는 몇몇 사람들을 위해 가치있는 부동산을 찾는 뉴런이 될 수 있는 것이다.
따라서 Rectifier activate function이 이용되어 100년이하의 집에는 아무런 가치가 존재하지 않고 100년이상일 때 더 오래될 수록 그 고전의 가치가 올라가도록 함수를 적용할 수 있는 것이다.
이전에 이야기했듯이 각각의 뉴런은 가격을 예측하기에는 너무 특수한 경우들이지만 이들이 힘을 합치면 대단한 정확도를 갖는 신경망을 구성해낼 수 있는것이다.
How do Neural Networks learn?
프로그램이 원하는 작동이 하도록 하는 방법은 각각의 상황마다 어떤 행동을 할지 결정해주는 hard coding과 입력값과 출력값에 대한 정보만 제공하고 신경망이 알아서 학습하도록 하는 NN을 이용하는 것이다. NN을 이용하기 위해 이를 어떻게 학습시킬지 알아볼 것이다.
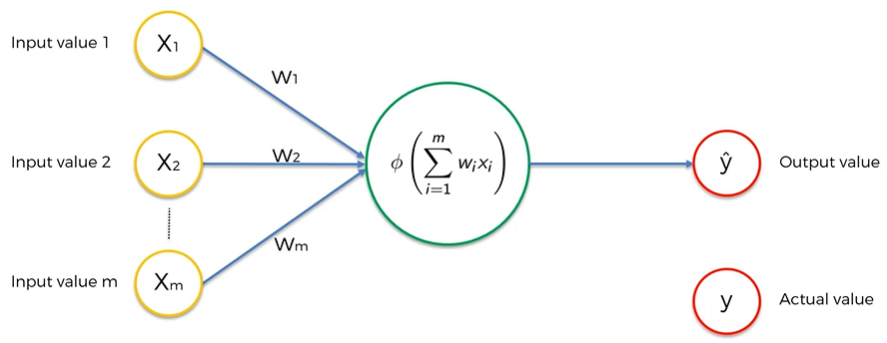
우선 perceptron이라고 불리는 단층 피드포워드 신경망 보자.
실제 값을 y라고 두기 때문에 ouput 값을 y hat으로 둔다. 여기서 부터 Coursera의 supervised machine learning에서 배웠던 내용이 많이 나왔다.

Cost function은 actual value와 output value의 차이 즉 오차를 계산하는 함수인데 이를 이용하여 보라색 화살표 방향으로 진행하여 가중치를 재조정하여 cost function을 줄이는 것이 목표이다. 같은 신경망에 data set을 반복하여 입력하고 가중치를 재조정하는 과정을 거쳐서 cost function을 낮추는데 이를 Backpropagation(역전파)라고 부른다.
Gradient Descent
Supervised Machine Learning 강의에서 꾀나 자세하게 학습했던 Gradient Descent가 결국은 역전파 과정에서 가중치를 조정하는 방법이라는 것을 알게 되었다.
무차별적으로 가중치를 조절하다보면 Curse of Dimensionality(차원의 저주)에 걸린다.
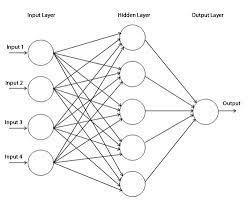
위와 같이 1개의 hidden layer만 존재하고 25개의 weights가 존재하는 정말 너무나도 단순한 perceptron에서 무차별 대입 방식을 이용해보자. 1000^25 즉 10^75가 나온다. 세상에서 가장 빠른 Sunway TaihuLight라는 세계에서 가장 빠른 슈퍼 컴퓨터를 기준으로 93Peta FLOPS의 연산속도를 갖고 있는데 일반 컴퓨터는 몇 기가FLOPS 정도의 속도를 갖고 있다. Sunway TaihuLight를 기준으로 잡아도 10^75/(93*10^15)로 러프하게 계산을 해보면 3.42*10^50년이 나온다. 이는 우주가 존재한 시간보다 길다. 따라서 무차별 대입 방식은 불가능한 것이다.
따라서 Gradient Descent(경사 하강법)라는 방식을 이용하도록 한다. 이전에 학습 했듯이 경사를 측정하여 우하향인지 좌하향인지 측정하여 방향을 결정하여 한단계씩 이동을 하여 최적점을 찾는 것이다. 자세한 내용은 Supervised Machine Learning의 Gradient Descent 글에 정리해 두었다.
Stochastic Gradient Descent
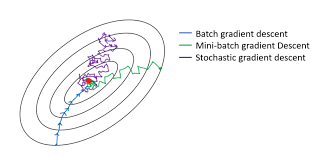
Stochastic Greadient Descent(확률적 경사 하강법, SGD)은 data set 전체를 한번에 이용하여 가중치 조절을 하는 것이 아니라 data set의 한 행을 하나씩 가중치 조절을 완료하고 다음 행을 조절하는 과정을 거친다. 이를 통해 local minimun에서 알고리즘이 멈추는 현상을 방지하여 global minimum을 찾는데 유리한 알고리즘이다. 하나씩 해야해서 오래 걸린다고 생각 할 수 있지만 사실 큰 data set을 한번에 컨트롤할 필요가 없어서 오히려 가벼운 알고리즘이다.
추가적으로 Mini-batch Gradient Descent는 본인이 설정한 숫자만큼의 data만 이용하는 방식이다.
Backpropagation
Backpropagation(역전파)는 Forwardpropagation을 통해 얻은 오차를 이용하여 역으로 가중치를 조정하는 것이다.
이는 굉장히 고급 알고리즘이다. 수학적인 방법을 이용하여 한번에 모든 가중치를 조절 할 수 있는 것이다.
'Robotics & AI > DeepLearning' 카테고리의 다른 글
| Udemy - 딥러닝의 모든 것(Softmax & Cross-Entropy) (0) | 2023.04.23 |
|---|---|
| Udemy - 딥러닝의 모든 것(CNN) (1) | 2023.04.06 |
| Pytorch Basic (0) | 2023.03.18 |
| Udemy - 딥러닝의 모든 것(ANN 구축하기) (0) | 2023.01.06 |
| Udemy - 딥러닝의 모든 것(Intro) (0) | 2022.12.27 |



