Intro
4/1부터 데이터 인텔리전스 연구실에서 학부연구생으로 연구활동에 참여하게 되어서 해당 연구실에서 최소한의 연구를 진행하기 위해 필요한 배경지식을 쌓는 과정의 일환으로 Pytorch에 대해 공부를 하고자한다. 파이토치의 라이브러리나 모듈 문법같은 내용은 아래 첨부한 링크인 위키독스에서 굉장히 잘 정리되어있기 때문에 개념적인 내용이나 새롭게 알게된 내용들 위주로 정리하고자한다.
Tensor
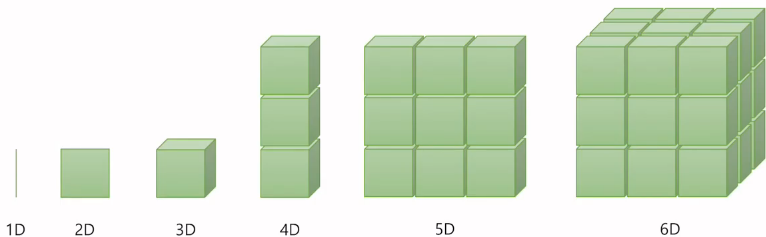
딥러닝에서 텐서란, 다차원 배열을 나타내는 데이터 구조이다.
텐서는 기본적으로 스칼라, 벡터, 행렬 등과 같은 다양한 차원의 배열을 나타낼 수 있으며, 딥러닝에서 입력 데이터, 가중치, 편향 등의 모든 데이터를 텐서로 표현한다. 예를들어 딥러닝에서 가중치와 편향을 표현할 때도 텐서를 사용하며, 이러한 텐서들은 딥러닝 모델의 학습과정에서 계산되어 업데이트된다. 따라서, 딥러닝에서 텐서는 중요한 개념 중 하나이며, 딥러닝 모델의 입력, 출력, 가중치, 편향 등 모든 데이터를 표현하기 위해 사용된다.
딥러닝에서는 일반적으로 1차원 텐서를 벡터, 2차원 텐서를 행렬, 3차원 이상의 텐서를 다차원 배열이라고 부르기도 한다. 따라서, 스칼라나 벡터와 같은 개념은 텐서의 일종으로 취급되며, 텐서의 차원과 크기에 따라 1차원 텐서, 2차원 텐서 등으로 표현된다.
딥 러닝을 할때 다루고 있는 행렬 또는 텐서의 크기를 고려하는 것은 항상 중요하다.
예를들어 2D Tensor는 다음과 같이 표기한다.
|t| = (Batch size, dim)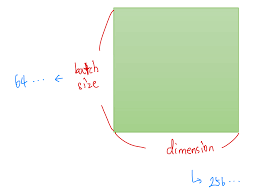
훈련 데이터 하나의 크기를 256이라고 하면 숫자들의 나열이 256의 길이로 있다고 상상하면된다. 훈련 데이터 하나 = 벡터의 차원이고 해당 값이 256이 된는 것이다. 만약 이런 훈련 데이터의 개수가 3000개라고 한다면, 현재 전체 훈련 데이터의 크기는 3,000 × 256이다. 3,000개를 1개씩 꺼내서 처리하는 것도 가능하지만 컴퓨터는 훈련 데이터를 하나씩 처리하는 것보다 보통 덩어리로 처리하기 때문에 3,000개에서 64개씩 꺼내서 처리한다고 한다면 이 때 batch size를 64라고 한다. 그렇다면 컴퓨터가 한 번에 처리하는 2D 텐서의 크기는 (batch size × dim) = 64 × 256이다.
NLP에서 3D Tensor는 다음과 같다.
|t| = (batch size, length, dim)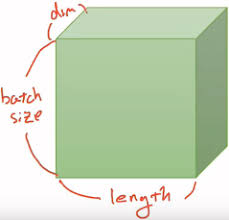
NLP의 예제를 통해 살펴보자.
[[나는 사과를 좋아해], [나는 바나나를 좋아해], [나는 사과를 싫어해], [나는 바나나를 싫어해]]위와 같은 4개의 문장으로 이루어진 훈련데이터가 있으면 아래와 같이 단어로 분리해주어 데이터를 만든다.
[['나는', '사과를', '좋아해'],['나는', '바나나를', '좋아해'],['나는', '사과를', '싫어해'],['나는', '바나나를', '싫어해']]이제 훈련 데이터의 크기는 4 × 3의 크기를 가지는 2D 텐서인데 이를 숫자로 변환하여 컴퓨터가 데이터 처리를 잘하도록 바꿔준다.
'나는' = [0.1, 0.2, 0.9]
'사과를' = [0.3, 0.5, 0.1]
'바나나를' = [0.3, 0.5, 0.2]
'좋아해' = [0.7, 0.6, 0.5]
'싫어해' = [0.5, 0.6, 0.7]위와 같은 인코딩 방식으로 데이터를 재구성하면 다음과 같다.
[[[0.1, 0.2, 0.9], [0.3, 0.5, 0.1], [0.7, 0.6, 0.5]],
[[0.1, 0.2, 0.9], [0.3, 0.5, 0.2], [0.7, 0.6, 0.5]],
[[0.1, 0.2, 0.9], [0.3, 0.5, 0.1], [0.5, 0.6, 0.7]],
[[0.1, 0.2, 0.9], [0.3, 0.5, 0.2], [0.5, 0.6, 0.7]]]이제 훈련 데이터는 4 × 3 × 3의 크기를 가지는 3D 텐서이다. 이제 batch size를 2로 해보면 다음과 같다.
batch #1
[[[0.1, 0.2, 0.9], [0.3, 0.5, 0.1], [0.7, 0.6, 0.5]],
[[0.1, 0.2, 0.9], [0.3, 0.5, 0.2], [0.7, 0.6, 0.5]]]
batch #2
[[[0.1, 0.2, 0.9], [0.3, 0.5, 0.1], [0.5, 0.6, 0.7]],
[[0.1, 0.2, 0.9], [0.3, 0.5, 0.2], [0.5, 0.6, 0.7]]]컴퓨터는 배치 단위로 가져가서 연산을 수행한다. 그리고 현재 각 배치의 텐서의 크기는 (2 × 3 × 3)이다.
이는 (batch size, 문장 길이, 단어 벡터의 차원)의 크기이다.
Numpy vs Pythorch
우선 다뤄보았던 numpy부터 보면 다음과 같다.
#numpy import
import numpy as np
#1차원 텐서
t = np.array([0., 1., 2., 3., 4., 5., 6.])
# 파이썬으로 설명하면 List를 생성해서 np.array로 1차원 array로 변환함.
print(t)
[0. 1. 2. 3. 4. 5. 6.]
#차원,크기 출력
print('Rank of t: ', t.ndim)
print('Shape of t: ', t.shape)
Rank of t: 1
Shape of t: (7,)
# 인덱스를 통한 원소 접근
print('t[0] t[1] t[-1] = ', t[0], t[1], t[-1])
t[0] t[1] t[-1] = 0.0 1.0 6.0
#슬라이싱
print('t[2:5] t[4:-1] = ', t[2:5], t[4:-1]) # [시작 번호 : 끝 번호]로 범위 지정을 통해 가져온다.
t[2:5] t[4:-1] = [2. 3. 4.] [4. 5.]
print('t[:2] t[3:] = ', t[:2], t[3:]) # 시작 번호를 생략한 경우와 끝 번호를 생략한 경우
t[:2] t[3:] = [0. 1.] [3. 4. 5. 6.]
#2차원 텐서
t = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.], [10., 11., 12.]])
print(t)
[[ 1. 2. 3.]
[ 4. 5. 6.]
[ 7. 8. 9.]
[10. 11. 12.]]
print('Rank of t: ', t.ndim)
print('Shape of t: ', t.shape)
Rank of t: 2
Shape of t: (4, 3)
이제 유사하지만 좀더 좋은 pytorch로 해보자.
#torch import
import torch
#1차원 텐서
t = torch.FloatTensor([0., 1., 2., 3., 4., 5., 6.])
print(t.dim()) # rank. 즉, 차원
print(t.shape) # shape
print(t.size()) # shape
1
torch.Size([7])
torch.Size([7])
print(t[0], t[1], t[-1]) # 인덱스로 접근
print(t[2:5], t[4:-1]) # 슬라이싱
print(t[:2], t[3:]) # 슬라이싱
tensor(0.) tensor(1.) tensor(6.)
tensor([2., 3., 4.]) tensor([4., 5.])
tensor([0., 1.]) tensor([3., 4., 5., 6.])
#2차원 텐서
t = torch.FloatTensor([[1., 2., 3.],
[4., 5., 6.],
[7., 8., 9.],
[10., 11., 12.]
])
print(t)
tensor([[ 1., 2., 3.],
[ 4., 5., 6.],
[ 7., 8., 9.],
[10., 11., 12.]])
print(t.dim()) # rank. 즉, 차원
print(t.size()) # shape
2
torch.Size([4, 3])
print(t[:, 1]) # 첫번째 차원을 전체 선택한 상황에서 두번째 차원의 첫번째 것만 가져온다.
print(t[:, 1].size()) # ↑ 위의 경우의 크기
tensor([ 2., 5., 8., 11.])
torch.Size([4])
print(t[:, :-1]) # 첫번째 차원을 전체 선택한 상황에서 두번째 차원에서는 맨 마지막에서 첫번째를 제외하고 다 가져온다.
tensor([[ 1., 2.],
[ 4., 5.],
[ 7., 8.],
[10., 11.]])Broadcasting
딥 러닝을 하게되면 불가피하게 크기가 다른 행렬 또는 텐서에 대해서 사칙 연산을 수행할 필요가 있는 경우가 생깁니다. 이를 위해 파이토치에서는 자동으로 크기를 맞춰서 연산을 수행하게 만드는 브로드캐스팅이라는 기능을 제공한다.
m1 = torch.FloatTensor([[3, 3]])
m2 = torch.FloatTensor([[2, 2]])
print(m1 + m2)
tensor([[5., 5.]])위처럼 크기가 같은 텐서끼리의 연산은 아무 문제가 없다.
# Vector + scalar
m1 = torch.FloatTensor([[1, 2]])
m2 = torch.FloatTensor([3]) # [3] -> [3, 3]
print(m1 + m2)
tensor([[4., 5.]])그러나 이렇게 벡터와 스칼라 같이 차원이 다른 텐서도 연산이 가능하다.
# 2 x 1 Vector + 1 x 2 Vector
m1 = torch.FloatTensor([[1, 2]])
m2 = torch.FloatTensor([[3], [4]])
# 브로드캐스팅 과정에서 실제로 두 텐서가 변경되는 과정
[1, 2]
==> [[1, 2],
[1, 2]]
[3]
[4]
==> [[3, 3],
[4, 4]]
print(m1 + m2)
tensor([4., 5.],
[5., 6.]])이런식으로 사이즈가 다른 텐서끼리도 자유롭게 resizing되어 연산을 가능케해준다.
그러나 보이는것 처럼 연산과정을 완벽히 이해하고 어떤식으로 자동변환이 되는지 생각하지 않으면 원하는 결과가 나왔을때 문제가 생긴 포인트를 잡기 힘들다.
추가적인 유용한 기능들
#행렬곱
m1 = torch.FloatTensor([[1, 2], [3, 4]])
m2 = torch.FloatTensor([[1], [2]])
print('Shape of Matrix 1: ', m1.shape) # 2 x 2
print('Shape of Matrix 2: ', m2.shape) # 2 x 1
print(m1.matmul(m2)) # 2 x 1
Shape of Matrix 1: torch.Size([2, 2])
Shape of Matrix 2: torch.Size([2, 1])
tensor([[ 5.],
[11.]])
#평균
t = torch.FloatTensor([1, 2])
print(t.mean())
tensor(1.5000)
t = torch.FloatTensor([[1, 2], [3, 4]])
print(t.mean())
tensor(2.5000)
#차원을 인자로 제공
print(t.mean(dim=0)) #첫번째 차원인 행을 제거
tensor([2., 3.])
print(t.mean(dim=1)) #두번째 차원인 열을 제거
tensor([1.5000, 3.5000])
#덧셈
t = torch.FloatTensor([[1, 2], [3, 4]])
print(t)
tensor([[1., 2.],
[3., 4.]])
print(t.sum()) # 단순히 원소 전체의 덧셈을 수행
print(t.sum(dim=0)) # 행을 제거
print(t.sum(dim=1)) # 열을 제거
print(t.sum(dim=-1)) # 열을 제거
tensor(10.)
tensor([4., 6.])
tensor([3., 7.])
tensor([3., 7.])
#최대와 아그맥스
t = torch.FloatTensor([[1, 2], [3, 4]])
print(t)
tensor([[1., 2.],
[3., 4.]])
print(t.max()) # Returns one value: max
tensor(4.)
print(t.max(dim=0)) # Returns two values: max and argmax
(tensor([3., 4.]), tensor([1, 1]))
[[1, 2],
[3, 4]]
첫번째 열에서 0번 인덱스는 1, 1번 인덱스는 3입니다.
두번째 열에서 0번 인덱스는 2, 1번 인덱스는 4입니다.
다시 말해 3과 4의 인덱스는 [1, 1]입니다.
만약 두 개를 함께 리턴받는 것이 아니라 max 또는 argmax만 리턴받고 싶다면 다음과 같이 리턴값에도 인덱스를 부여하면 됩니다. 0번 인덱스를 사용하면 max 값만 받아올 수 있고, 1번 인덱스를 사용하면 argmax 값만 받아올 수 있습니다.
print('Max: ', t.max(dim=0)[0])
print('Argmax: ', t.max(dim=0)[1])
Max: tensor([3., 4.])
Argmax: tensor([1, 1])
이번에는 dim=1로 인자를 주었을 때와 dim=-1로 인자를 주었을 때를 보겠습니다.
print(t.max(dim=1))
print(t.max(dim=-1))
(tensor([2., 4.]), tensor([1, 1]))
(tensor([2., 4.]), tensor([1, 1]))최대(Max)는 원소의 최대값을 리턴하고, 아그맥스(ArgMax)는 최대값을 가진 인덱스를 리턴합니다.
'Robotics & AI > DeepLearning' 카테고리의 다른 글
| Udemy - 딥러닝의 모든 것(Softmax & Cross-Entropy) (0) | 2023.04.23 |
|---|---|
| Udemy - 딥러닝의 모든 것(CNN) (1) | 2023.04.06 |
| Udemy - 딥러닝의 모든 것(ANN 구축하기) (0) | 2023.01.06 |
| Udemy - 딥러닝의 모든 것(ANN) (0) | 2022.12.27 |
| Udemy - 딥러닝의 모든 것(Intro) (0) | 2022.12.27 |



