최적 이진 탐색 트리
이진 탐색 트리(BST)는 루트의 왼쪽 서브트리에 있는 원소의 키 값은 루트보다 작고, 루트의 오른쪽 서브트리에 있는 원
소의 키 값은 루트보다 큰 이진 트리이다.
최적 이진 탐색 트리 문제는 트리 내의 키와 각 키가 탐색될 확률이 주어져 있을 때 그 트리의 평균 탐색 비용, 즉, 평균 비교
횟수를 계산하고 이를 최소화하는 탐색 트리를 구축하는 문제이다.
예를들어 키의 값이 A: 0.1 B: 0.3 C:0.6이면 아래와 같이 다양한 케이스의 트리에서 탐색비용을 계산해볼 수 있다.
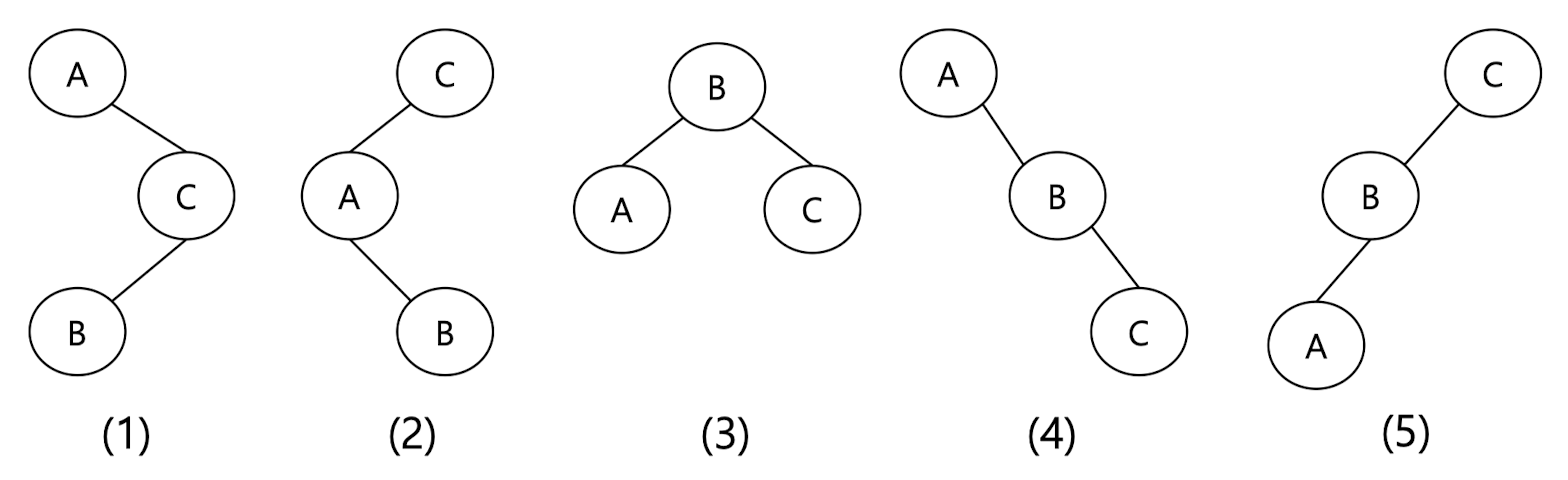
1번만 살펴보면 A를 탐색할때 0.1, C를 탐색할때 0.1+0.6, B를 탐색할때 0.1+0.6+0.3이 되어 3*0.1+2*0.6+1*0.3=1.8이 된다.
키 값 a_i ≤ a_i+1 ≤ … ≤ a_j 일 경우 A[i,j]는 이진 탐색 트리의 i부터 j까지의 노드에 대한 최소 평균 탐색 시간이다. 이를 DP, 즉 분할 정복을 위해 아래와 같이 이용하는 것이다.
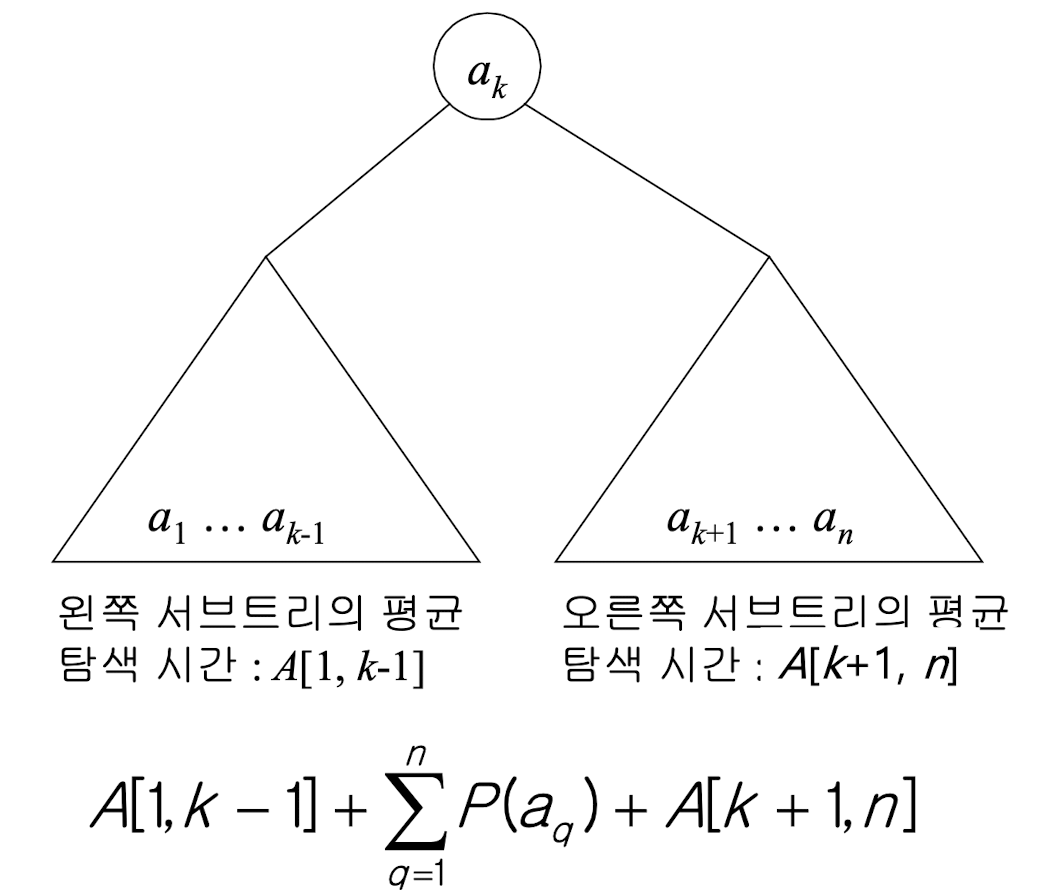
점화식을 정리해보면 아래와 같다.

첫번째 식은 기본 규칙이고 두번째 식은 하나밖에 안남은 경우 해당 확률 자체를 사용하겠다는 뜻이다. 마지막 식은 범위의 뒤쪽이 앞쪽을 넘어가면 0으로 만들어버려서 사용하지 못하도록 하는 것이다. 이를 간단히 말하면 위와 같은 사각형에서 upper 삼각형만 이용하겠다는 것이다.
예시로 a1 = A, a2 = B, a3 = C, a4= D이고 각각의 확률이 p1 = 0.1, p2 = 0.2, p3 = 0.3, p4 = 0.4인 경우를 살펴보자.
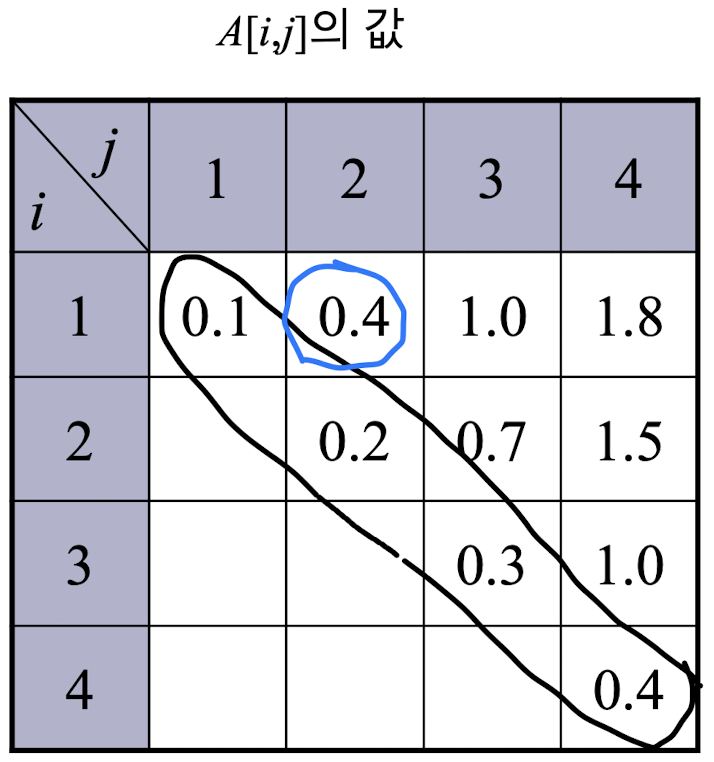
정답 표는 위와 같이 되는데 [1, 2]의 경우를 살펴보자.
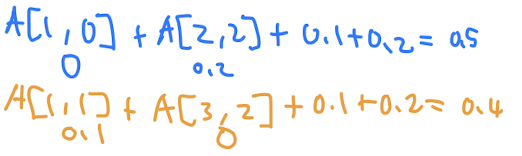
k가 1인 경우에는 0.5이고 k가 2인 경우에는 0.4여서 k가 2인 경우가 최적 탐색 경로가 되는 것이다.
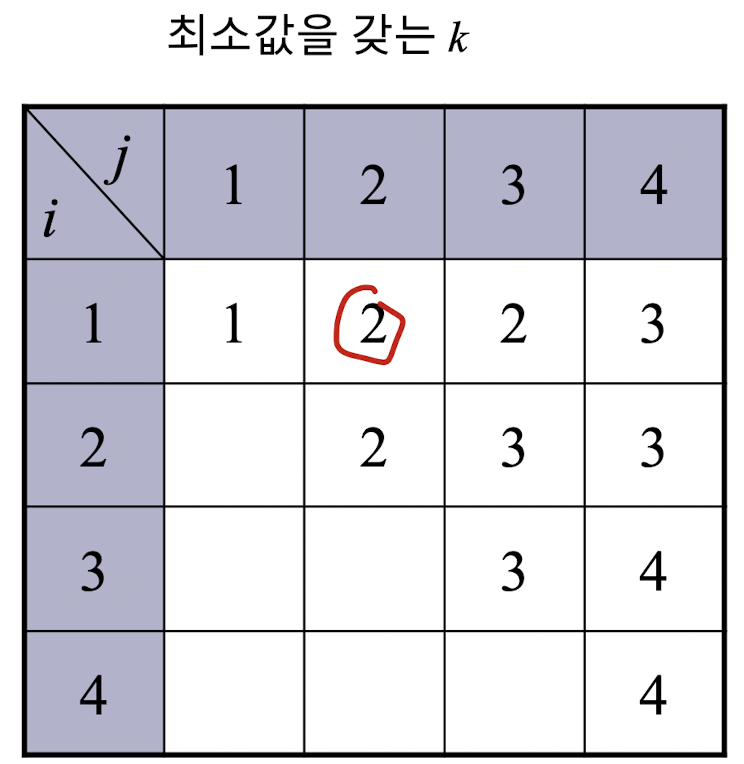
해당 알고리즘 코드를 살펴보면 아래와 같다.
OptimalBST(p[], r[], n)
{
for (i ← 1; i ≤ n; i ← i + 1) do {
A[i,i] ← p[i];
r[i,i] ← i;
}
for (h ← 1; h < n; h ← h + 1) do
for (i ← 1; i ≤ n-h; i ← i + 1) do {
j ← i + h;
A[i,j] ← mini≤k≤j(A[i,k-1] + A[k+1,j] + Σ P[m]);
r[i,j] ← 최소 값을 갖는 k;
}
return A[1,n];
}end OmtimalBST()
node_pointer BuildTree( i, j )
{
index k;
node_pointer p;
k = r[i][j];
if(k==0) return;
else{
p = new node_pointer;
p -> key = Key[k];
p -> left = BuildTree( i, k-1 );
p -> right = BuildTree( k+1, j );
return p;
}
}end BuildTree()
'Quality control (Univ. Study) > Algorithm Design' 카테고리의 다른 글
| Algorithm design - TSP(Traveling Salesperson Problem) (0) | 2024.05.21 |
|---|---|
| 알고리즘 설계 실습 - 연쇄 행렬 곱셈 (0) | 2024.05.16 |
| 알고리즘 설계 실습 - 삼각분할 (0) | 2024.05.08 |
| Algorithm design - Matrix-chain Multiplication (0) | 2024.05.07 |
| Algorithm design - DP / Levenshtein Distance (1) | 2024.05.02 |



