Kernel Support Vector Machine
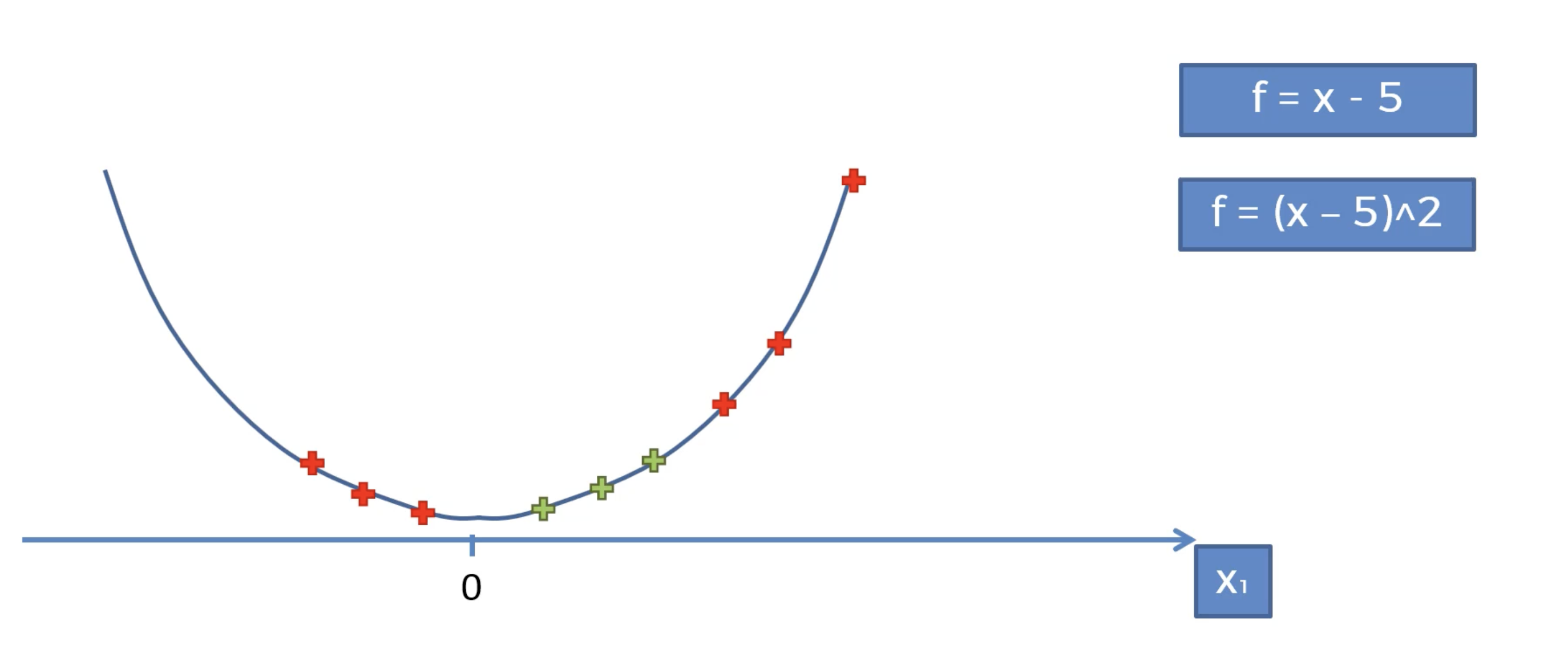
우선 간단한 1차원 상황부터 보면 다음과 같은 경우에는 선형적인 선을 통해 데이터를 분류할 수 없다.

따라서 f = (x-5)^2 함수에 값을 얹어서 선형적으로 분류할 수 있도록 다음과 같이 바꾼다.
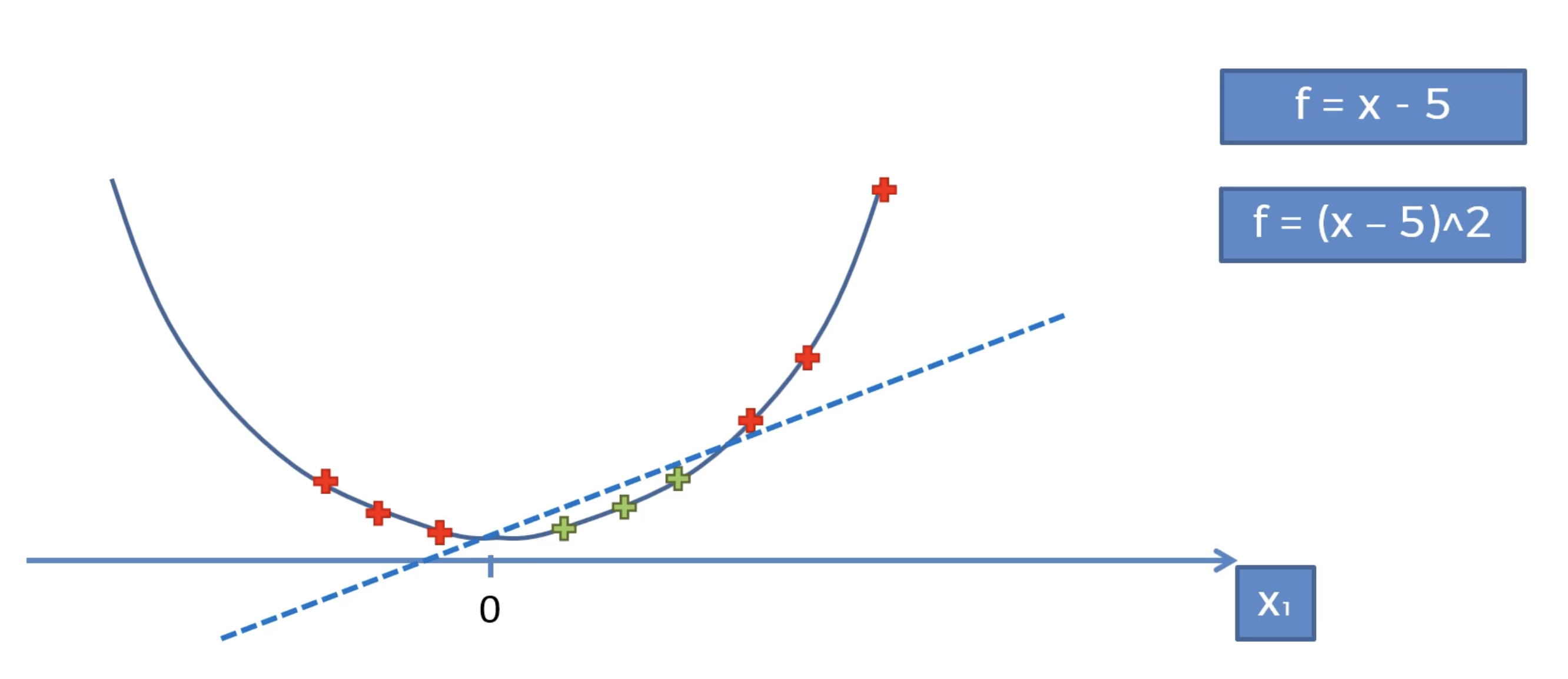
이제 linear한 점선으로 데이터가 분리됨을 볼 수 있다.
이를 좀더 고차원에서 살펴보면 다음과 같다.
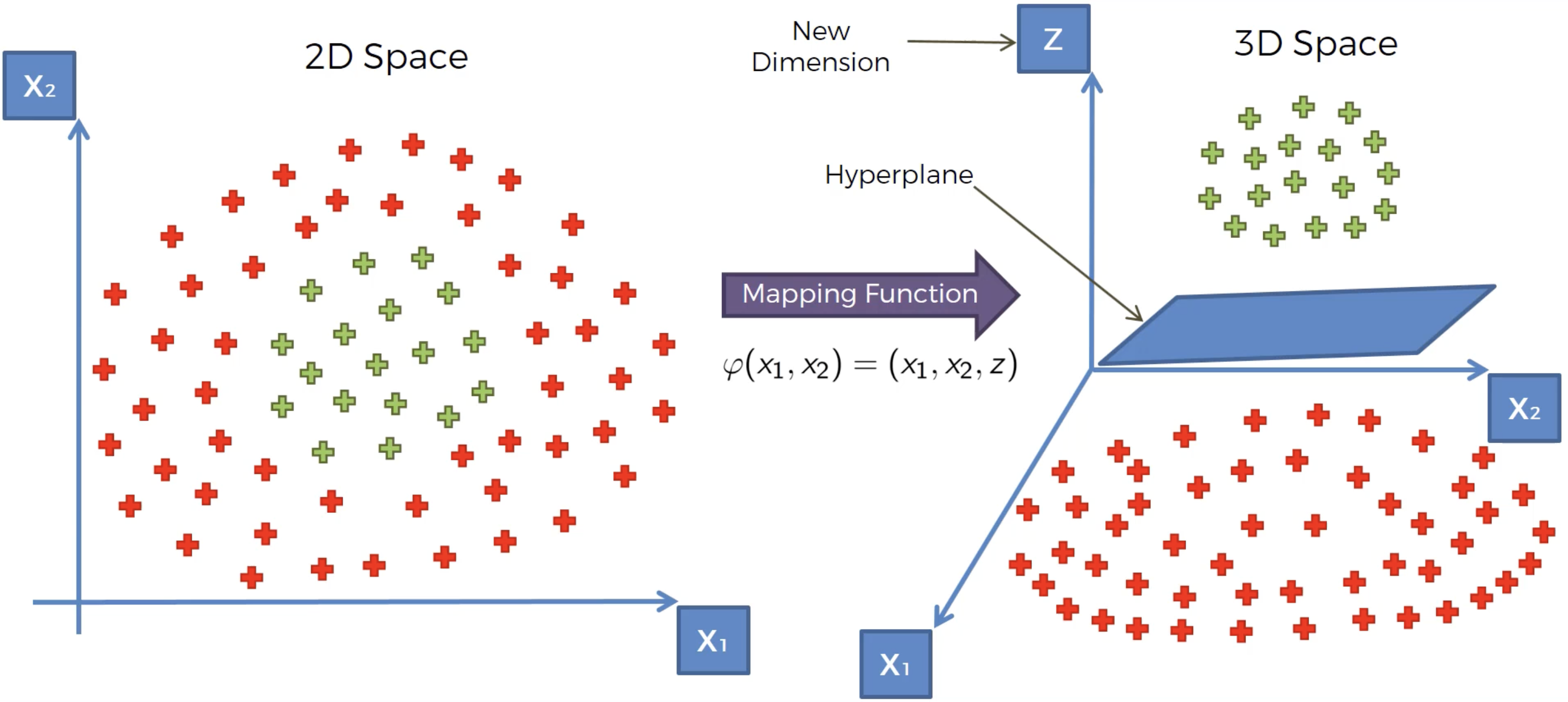
살펴보면 z라는 새로운 차원이 생겼고 데이터들은 Hyperplane으로 나뉘어짐을 볼 수 있다.
추후에 다시 2차원으로 projection을 하면 다음과 같이 비선형 분리기가 생김을 알 수 있다.
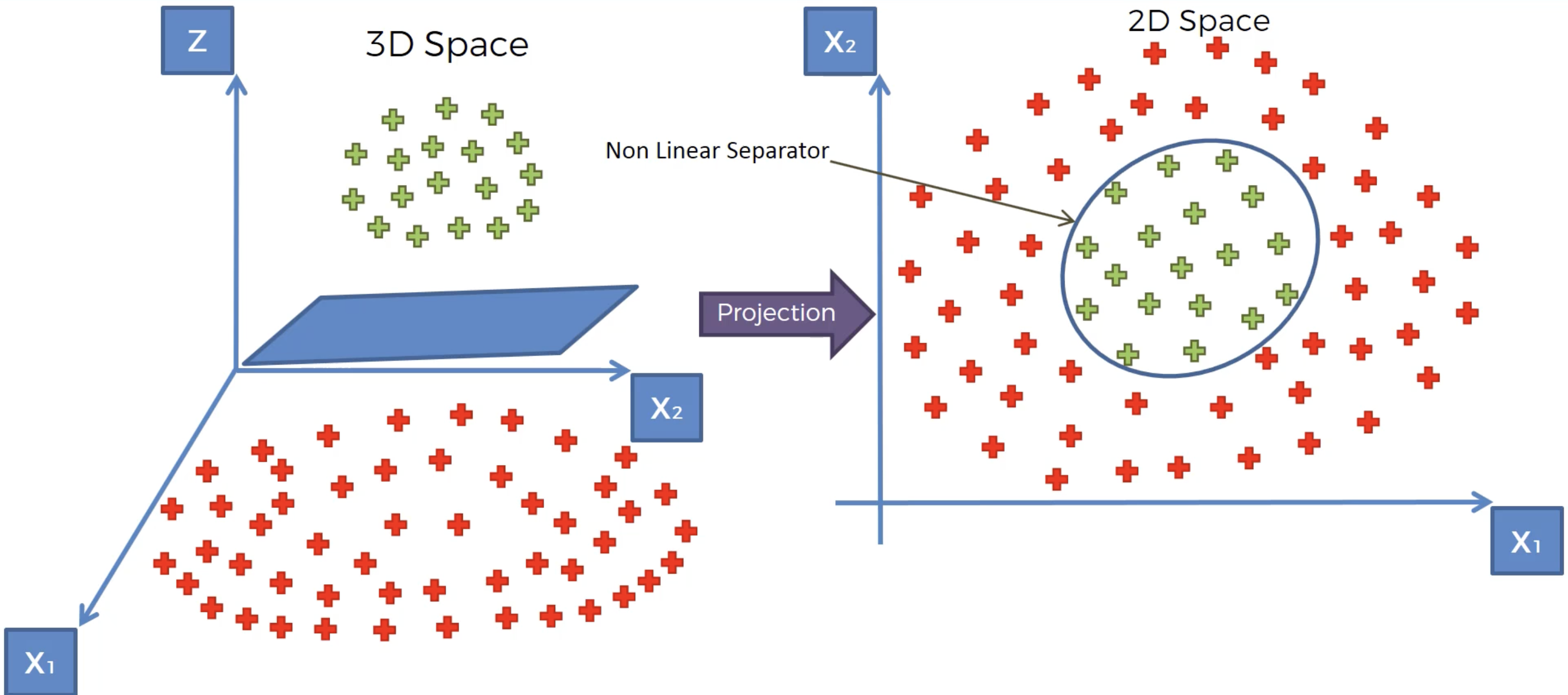
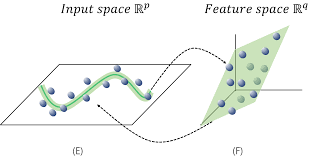
그러나 이렇게 고차원에서 연산을 진행하고 다시 저차원으로 내리는 과정은 컴퓨터에게도 굉장히 버거운 연산이라 속도면에서 단점이 존재할 수 있다. 따라서 더 효율적으로 비슷한 효과를 내는 방법이 고안되었다.
Kernel Trick
우선 Gaussian RBF Kernel을 살펴보자.

K는 커널을 의미하고 x벡터는 데이터 집합에서의 일종의 포인트이고 L벡터는 랜드마크를 의미한다.
절대값을 두번씌운것 같은 기호는 두 벡터 사이의 거리를 의미한다.
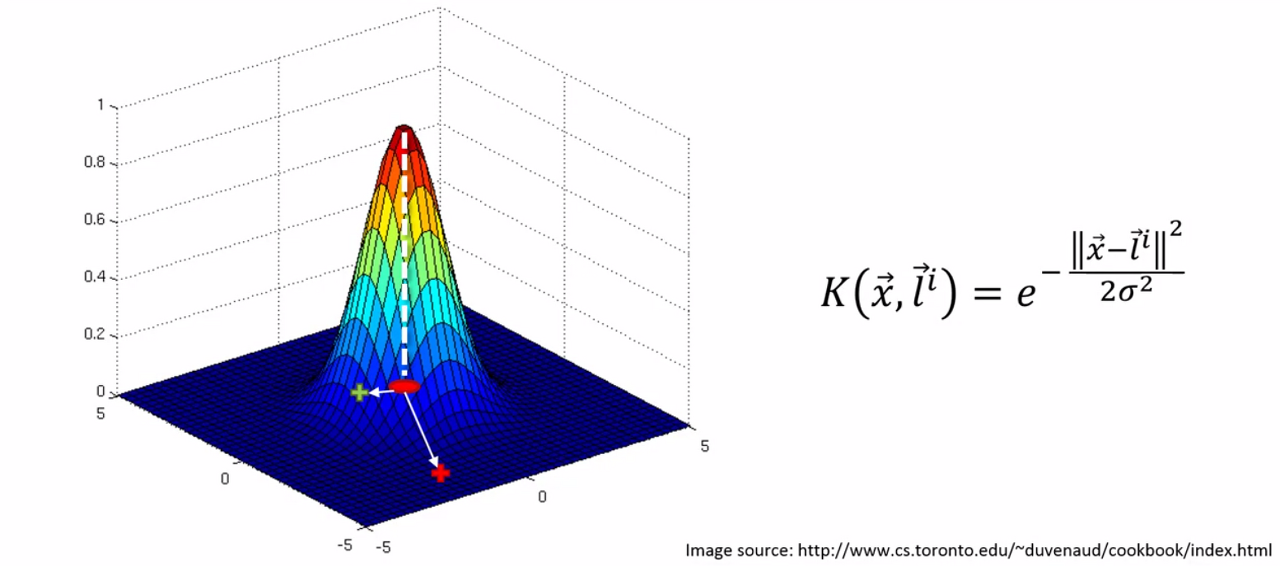
그리고 해당 식은 다음과 같이 그래프로 표현된다. 꼭지점이 되는 지점이 랜드마크 지점이라고 했을 때 랜드마크로 부터 벡터가 멀어지면 급격하게 그 값이 0에 수렴하게 하락함을 볼 수 있다. 이는 거리의 제곱이 e에 음수가 붙은 채로 지수 역할을 하므로 당연하다고 할 수 있다.
커널함수는 다음과 같이 이용된다.

데이터의 구성에 따라 적절하게 랜드마크 지점을 설정하고 시그마 값을 조절하여 경계의 크기를 조절하면 적절한 구분선을 구성할 수 있다.
이러한 방식을 이용하면 실제로 고차원으로 데이터를 재구성할 필요가 없어진다.
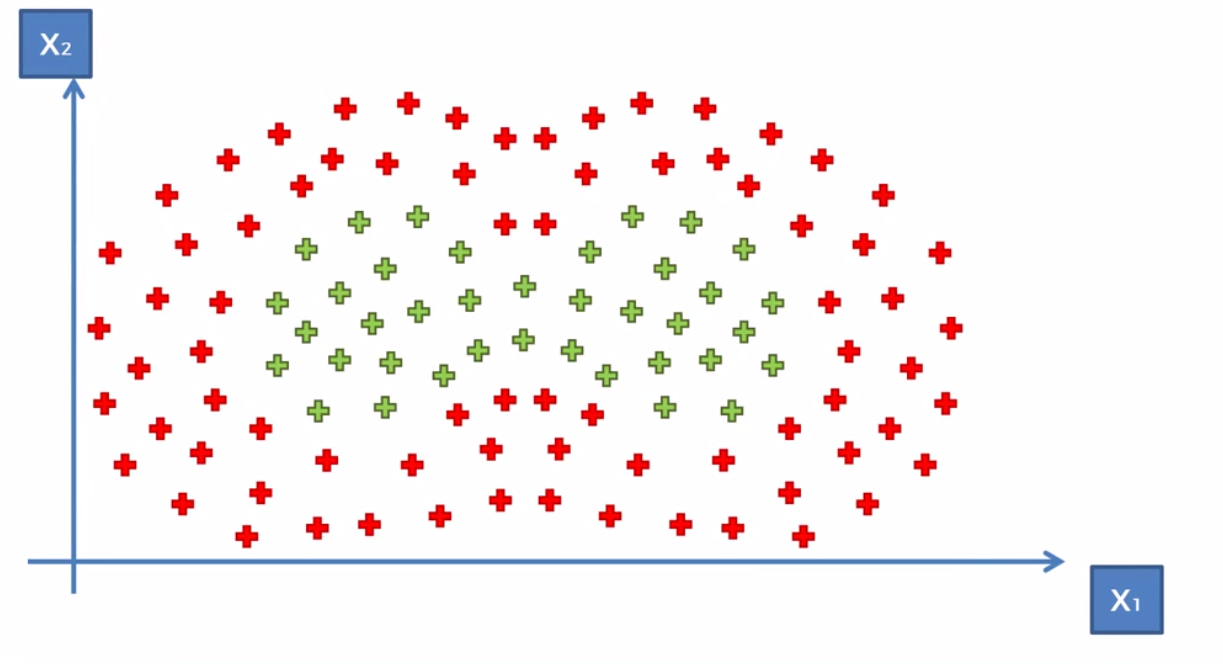
위와 같이 데이터가 조금 복잡하게 구성이 되어있다면 다음과 같이 커널함수를 더하는 방식으로 해결할 수 있다.

Type of Kernels
가장 많이 쓰이는 커널들은 다음과 같이 Gaussian RBF, Sigmoid, Polynomial 정도로 추릴 수 있다.

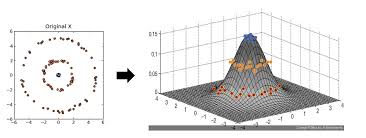
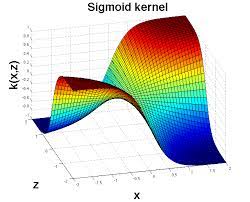
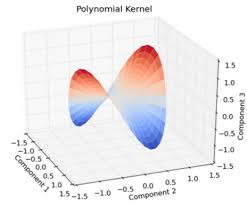
위의 커널들을 이용하여 아래오 같은 비선형적인 데이터들을 고차원으로 올린후에 해당 데이터를 회귀 분석할 수 있는 적절한 평면을 설정하고 다시 저차원으로 내리면 결국 비선형적인 회귀 곡선이 완성되는것을 볼 수 있다.
'Drawing (AI) > MachineLearning' 카테고리의 다른 글
| Udemy - 머신러닝의 모든 것 (Naive Bayes) (0) | 2023.06.20 |
|---|---|
| Udemy - 머신러닝의 모든 것 (Kernel SVM - 2) (0) | 2023.04.30 |
| Udemy - 머신러닝의 모든 것 (SVM) (0) | 2023.04.02 |
| Udemy - 머신러닝의 모든 것 (K-NN) (0) | 2023.03.31 |
| Udemy - 머신러닝의 모든 것 (로지스틱 회귀) (1) | 2023.03.26 |



