Logistic Regression
다양한 회귀들에 대해서 배웠다. 그러나 다음과 같은 경우에 어떤식으로 회귀를 진행해야할지 전혀 감이 잡히지 않는다.

원래알고있던 회귀를 이용하면 굉장히 이상한 결과가 나온다. 사실 이런 데이터는 기업에서 본인들의 상품을 선택한 사람에 대한 데이터와 같이 yes or no인 겨우 많이 보일 수 있는 데이터인데 지금까지 배운 지식으로는 어떤 모델을 써야할지 판단할 수 없다.
이때 아래의 sigmoid함수와 수학적 식을 이용하여 만들어진 logistic regression function을 이용할 수 있다.

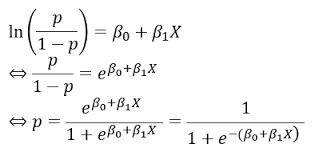
Customer Prediction
고객의 나이와 추정수입을 통해 제품을 구매할 손님인지 구매하지 않을 손님인지 예측을 해보도록 하자 이는 실제 세계에서도 있을 법한
모델로 보인다. 예측을 제대로 진행하면 타겟층에 맞춰서 SNS같은 곳에서 맞춤광고를 설정하여 적은 비용으로 높은 광고효과를 낼 수 있기 때문이다.

독립변수는 나이와 추정 수입, 종속변수는 과거 구매 여부이다.
#Logistic Regression
#Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
#Importing the dataset
dataset = pd.read_csv('Social_Network_Ads.csv')
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values
#Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
#Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)우선 feature scaling과정까지는 이전의 모델들과 다를게 없다. 한가지점이 있다면 test_size에서 보통은 무난하게 적합한 0.2를 채용했는데 이번에는 데이터 사이즈가 400이라 training: 300, test: 100으로 딱떨어지도록 0.25를 선택했다는 점이다. 대단하게 중요한 내용은 아닌 것으로 보인다.
[ 0.08648817 1.05583366]
[-0.11157634 -0.3648304 ]
[-1.20093113 0.07006676]
[-0.30964085 -1.3505973 ]
[ 1.57197197 1.11381995]
[-0.80480212 -1.52455616]
[ 0.08648817 1.8676417 ]
[-0.90383437 -0.77073441]
[-0.50770535 -0.77073441]
[-0.30964085 -0.91570013]
[ 0.28455268 -0.71274813]
[ 0.28455268 0.07006676]
[ 0.08648817 1.8676417 ]
[-1.10189888 1.95462113]
[-1.6960924 -1.5535493 ]
[-1.20093113 -1.089659 ]
[-0.70576986 -0.1038921 ]
[ 0.08648817 0.09905991]
[ 0.28455268 0.27301877]
[ 0.8787462 -0.5677824 ]
[ 0.28455268 -1.14764529]
[-0.11157634 0.67892279]
[ 2.1661655 -0.68375498]
[-1.29996338 -1.37959044]
[-1.00286662 -0.94469328]
[-0.01254409 -0.42281668]
[-0.21060859 -0.45180983]
[-1.79512465 -0.97368642]
[ 1.77003648 0.99784738]
[ 0.18552042 -0.3648304 ]
[ 0.38358493 1.11381995]feature scaling결과를 한번 보면 나이와 추정연봉이 일정한 범위로 scaling된 것을 볼 수 있다.
#Training the Logistic Regression model on the Training set
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(random_state = 0)
classifier.fit(X_train, y_train)
#Predicting a new result
print(classifier.predict(sc.transform([[30,87000]])))
print(classifier.predict_proba(sc.transform([[30,87000]])))
[0]
[[0.88725351 0.11274649]]학습시키는 과정도 전과 같았다. 30대의 연봉 87000인 사람에 대해서 새로운 예측을 실행하니 제대로 나오는 것을 볼 수 있었다.
이때 예측은 두가지 방식으로 진행해봤는데 하나는 predict로 최종 결과인 0 또는 1로 출력을 하는 것이고 다른 하나는 predict_proba로 로지스틱회귀 곡선상의 값을 특정지어 확률이 정확히 얼만큼인지 출력해주는 함수이다.
#Predicting the Test set results
y_pred = classifier.predict(X_test)
print(np.concatenate((y_pred.reshape(len(y_pred),1), y_test.reshape(len(y_test),1)),1))
[0 0]
[0 0]
[1 1]
[0 0]
[0 0]
[1 1]
[0 0]
[1 1]
[1 1]
[0 0]
[0 0]
[0 0]
[1 1]
[0 1]
[0 0]
[0 0]
[0 1]
[0 0]
[0 0]
[1 1]
[0 0]
[0 1]
[0 0]
[1 1]
[0 0]
[0 0]
[0 0]
[0 0]
[1 1]
[0 0]
[0 0]
[0 1]
[0 0]
[0 0]위는 test set에서 예측을 해본 결과인데 그 결과가 적절하게 나왔음을 알 수 있다.
#Making the Confusion Matrix
from sklearn.metrics import confusion_matrix, accuracy_score
cm = confusion_matrix(y_test, y_pred)
print(cm)
accuracy_score(y_test, y_pred)
[[65 3]
[ 8 24]]
0.89confusion matrix는 classification에서 모델을 평가하는 방법이다.
위처럼 결과가 2X2 행렬로 나오는데 그 값들은 다음과 같은 네개의 값이다.
- True Positives (TP): The number of positive instances that were correctly predicted as positive.
- False Positives (FP): The number of negative instances that were incorrectly predicted as positive.
- True Negatives (TN): The number of negative instances that were correctly predicted as negative.
- False Negatives (FN): The number of positive instances that were incorrectly predicted as negative.
위의 경우로 보면 실제로 산 사람은 73명인데 65명은 산다고 제대로 예측했지만 8명은 안살것이라고 잘못 예측했다. 다음으로 실제로 사지않은 사람 27명중 24명은 실제로 사지 않을 것이라고 제대로 예측했지만 3명은 살것이고 잘못 예측했다.
그에 따른 accuracy_score은 0.89로 나왔다.
#Visualising the Training set results
from matplotlib.colors import ListedColormap
X_set, y_set = sc.inverse_transform(X_train), y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 10, stop = X_set[:, 0].max() + 10, step = 0.25),
np.arange(start = X_set[:, 1].min() - 1000, stop = X_set[:, 1].max() + 1000, step = 0.25))
plt.contourf(X1, X2, classifier.predict(sc.transform(np.array([X1.ravel(), X2.ravel()]).T)).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('salmon', 'dodgerblue')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], c = ListedColormap(('salmon', 'dodgerblue'))(i), label = j)
plt.title('Logistic Regression (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()Training set에대한 시각화 결과

#Visualising the Test set results
from matplotlib.colors import ListedColormap
X_set, y_set = sc.inverse_transform(X_test), y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 10, stop = X_set[:, 0].max() + 10, step = 0.25),
np.arange(start = X_set[:, 1].min() - 1000, stop = X_set[:, 1].max() + 1000, step = 0.25))
plt.contourf(X1, X2, classifier.predict(sc.transform(np.array([X1.ravel(), X2.ravel()]).T)).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('salmon', 'dodgerblue')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], c = ListedColormap(('salmon', 'dodgerblue'))(i), label = j)
plt.title('Logistic Regression (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
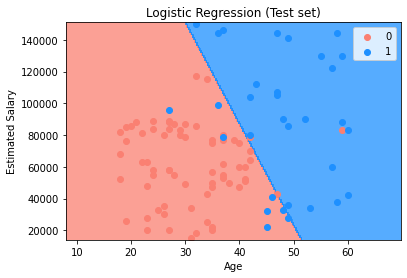
plt.show()Test set에대한 시각화 결과
'Robotics & AI > MachineLearning' 카테고리의 다른 글
| Udemy - 머신러닝의 모든 것 (SVM) (0) | 2023.04.02 |
|---|---|
| Udemy - 머신러닝의 모든 것 (K-NN) (0) | 2023.03.31 |
| Udemy - 머신러닝의 모든 것 (회귀 모델 선택) (0) | 2023.03.23 |
| Udemy - 머신러닝의 모든 것 (회귀 모델 성능 평가) (0) | 2023.03.20 |
| Udemy - 머신러닝의 모든 것 (Random Forest Regression) (0) | 2023.03.18 |



