Method of Cryptography
Cryptanalysis는 암호 해독 또는 암호 알고리즘의 약점을 찾아내는 과정을 말한다. 주요 방법은 다음과 같다.
- 단일 메시지의 해독 (Break a single message)
암호화된 하나의 메시지를 해독하는 것을 목표로 한다. - 암호화된 메시지에서 패턴 인식 (Recognize patterns in encrypted messages)
암호화된 메시지의 패턴을 찾아내어 의미 있는 정보를 추출한다. - 암호 해독 없이 의미 추론 (Infer some meaning without breaking the encryption)
메시지의 길이나 빈도와 같은 정보를 기반으로 암호를 해독하지 않고도 의미를 유추한다. - 키 유추 (Easily deduce the key)
한 메시지를 해독한 후 동일한 키를 사용해 이후 메시지도 해독할 수 있는 경우를 말한다. - 암호 구현 또는 환경의 취약점 발견 (Find weaknesses in the implementation or environment)
암호화 시스템이 구현되는 과정이나 사용 환경에서의 약점을 탐색한다. - 암호 알고리즘의 일반적 약점 발견 (Find general weaknesses in an encryption algorithm)
암호 알고리즘 자체에 존재하는 구조적 약점을 찾아낸다.
암호 공격
- Ciphertext Only (암호문만 제공되는 경우)
암호문만 제공된 상황에서, 암호 해독자는 여러 암호화된 메시지 간의 패턴, 유사성, 불연속성을 분석하여 암호를 해독하려고 시도한다. 이는 암호화 방법의 약점을 찾는 가장 일반적인 접근 방식 중 하나이다. - Plaintext와 Ciphertext 동시 제공 (평문과 암호문 제공되는 경우)
평문(Plaintext)과 암호문(Ciphertext)이 모두 주어진 경우, 암호 해독자는 변환 과정을 분석하여 암호화 알고리즘의 내부 동작을 이해하려고 한다.- Known Plaintext (알려진 평문 공격): 이미 알려진 평문에 해당하는 암호문이 제공된 경우, 이를 활용하여 암호화 알고리즘의 패턴이나 키를 찾아내려고 한다.
- Chosen Plaintext (선택된 평문 공격): 공격자가 특정 평문을 선택해 암호화 과정을 거친 암호문을 생성한 후, 이를 분석하여 암호화 알고리즘의 동작을 해독한다.
- Chosen Ciphertext (선택된 암호문 공격): 선택된 암호문을 복호화를 마구마구 진행하여 암호 알고리즘의 약점을 탐색하는 방법이다.
One-Time Pads(OTP)
일회성 패드(One-Time Pad)는 이론상으로 완벽한 보안 기능을 제공한다.

- 입력 데이터
- 평문(Plaintext): 암호화하고자 하는 원본 데이터이다.
- 키(Key): 반복되지 않는 긴 숫자 시퀀스(난수)로 구성되며, 암호화와 복호화에 동일하게 사용된다.
- 암호화 과정
- 평문의 각 비트와 키의 해당 비트를 배타적 논리합(XOR) 연산으로 결합한다.
- 이 연산을 통해 암호문(Ciphertext)이 생성된다.
- 암호문은 원본 데이터와 키의 조합 결과로 완전히 임의화된다.
- 복호화 과정
- 암호문과 동일한 키를 다시 XOR 연산에 사용하여 원래의 평문을 복원한다.
- 이는 XOR 연산의 특성상 두 번 연속으로 동일한 연산을 수행하면 원래의 입력으로 복원되는 원리에 기반한다.
- 완벽한 보안
- 키가 충분히 길고 절대 반복되지 않으며, 비밀리에 안전하게 공유되었을 경우, 이 암호 방식은 정보 이론적으로 절대 해독할 수 없다.
- 즉, 암호문만으로는 원래의 평문에 대한 어떠한 정보도 얻을 수 없다.

그러나 실제로는 key를 안전하게 공유할 수 없다는 문제 때문에 현실적으로는 불가능하다. 만약 key완벽하게 안전하게 보낼 수 있다면 OTP가 왜 필요하겠는가 key를 보내는 방법으로 메세지를 보내면 되는 것을...
Shannon’s Characteristics of Good Ciphers
Claude Shannon이 제안한 좋은 암호의 특징은 다음과 같다.
- 필요한 비밀성에 따라 암호화 및 복호화 작업의 양이 결정되어야 한다
- 암호화와 복호화에 필요한 작업량은 데이터의 민감성과 비밀성을 기준으로 적절하게 조정되어야 한다.
- 키와 암호화 알고리즘의 구성은 복잡성을 피해야 한다
- 암호화 알고리즘과 키는 불필요하게 복잡하지 않아야 하며, 보안을 유지하면서도 간단하게 설계되어야 한다.
- 암호화 프로세스의 구현은 가능한 한 간단해야 한다
- 암호화 및 복호화 과정이 지나치게 복잡하면 오류 가능성이 높아지고 효율성이 떨어지므로 간단하게 구현되어야 한다.
- 암호화 과정에서 발생한 오류는 추가 정보의 손상으로 이어지지 않아야 한다
- 암호화 오류가 다른 부분의 데이터를 손상시키거나 추가적인 정보 손실을 야기하지 않도록 설계되어야 한다.
- 암호화된 텍스트의 크기는 원본 텍스트의 크기를 초과하지 않아야 한다
- 암호화 과정에서 데이터의 크기가 지나치게 커지면 저장 및 전송 효율성이 떨어지므로 원본 텍스트와 유사한 크기로 유지되어야 한다.
신뢰할 수 있는 암호 시스템의 특징은 아래와 같다.
- 수학적 기반이 탄탄해야 한다 (It is based on sound mathematics)
- 신뢰할 수 있는 암호 시스템은 검증된 수학적 이론을 기반으로 설계되어야 한다.
- 이는 암호화와 복호화 과정이 논리적이고 안전한 방식으로 이루어지도록 보장한다.
- 전문가의 검토와 안전성 검증을 거쳐야 한다 (It has been analyzed by competent experts and found to be sound)
- 암호 시스템은 암호학 전문가들에 의해 철저히 분석되고 검증되어야 한다.
- 전문가들이 문제없이 작동한다고 평가한 시스템만이 신뢰할 수 있다.
- 시간의 시험을 견뎌야 한다 (It has stood the test of time)
- 효과적인 암호 시스템은 시간이 지나도 여전히 안전성을 유지해야 한다.
- 이는 잠재적 공격 시도와 발전된 기술에도 취약하지 않다는 것을 의미한다.
DES Algorithm
DES(Data Encryption Standard)는 블록 암호 방식의 대칭 키 암호화 알고리즘이다. 주요 과정은 다음과 같다.

- 입력 데이터 분할
- 64비트의 입력 데이터를 Left Half(왼쪽 절반)와 Right Half(오른쪽 절반)로 나눈다.
- 각 절반은 32비트로 구성된다.
- 오른쪽 절반 확장 (Expansion Permutation)
- 오른쪽 절반의 32비트를 48비트로 확장한다.
- 이 과정은 데이터의 혼란성과 확산성을 증가시키기 위한 것이다.
- 키 생성 및 적용
- 56비트 키를 사용하여 48비트 서브키(Subkey)를 생성한다.
- 이 서브키와 확장된 오른쪽 절반 데이터를 XOR 연산으로 결합한다.
- 대체(Substitution)와 재배열(Permuted Choice)
- XOR 연산 결과는 S-Box(Substitution Box)를 통해 32비트로 변환된다.
- 변환된 데이터는 Permutation 과정을 통해 다시 섞인다.
- 새로운 데이터 구성
- Permutation 결과를 XOR 연산으로 왼쪽 절반 데이터와 결합하여 새로운 오른쪽 절반을 생성한다.
- 기존 오른쪽 절반은 새로운 왼쪽 절반으로 이동한다.
- 반복(Round)
- 위 과정을 총 16라운드 반복하여 암호화를 완성한다.
- 최종 암호문 출력
- 마지막 라운드 결과를 병합하고 최종 Permutation을 적용하여 암호문(Ciphertext)을 생성한다.
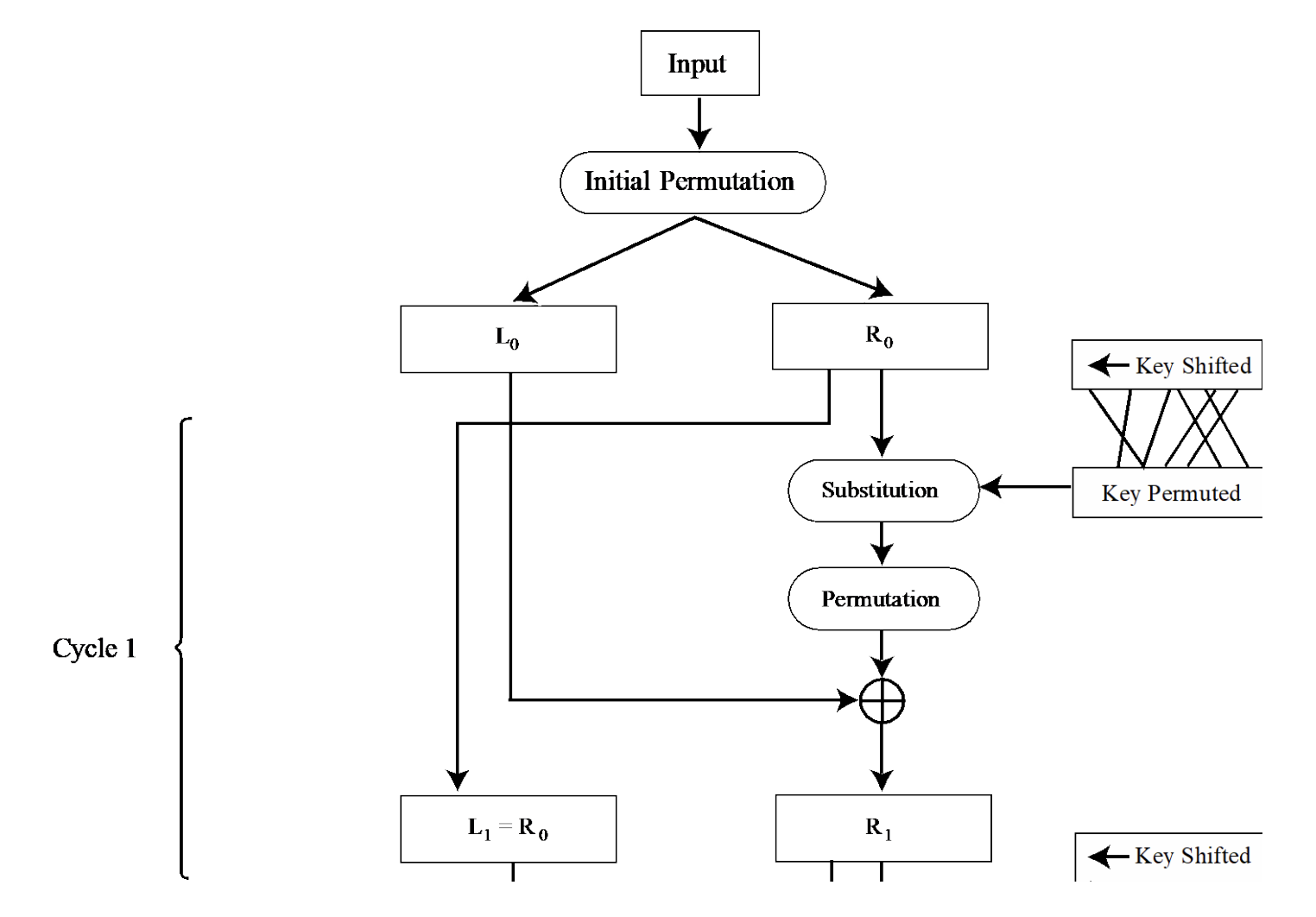
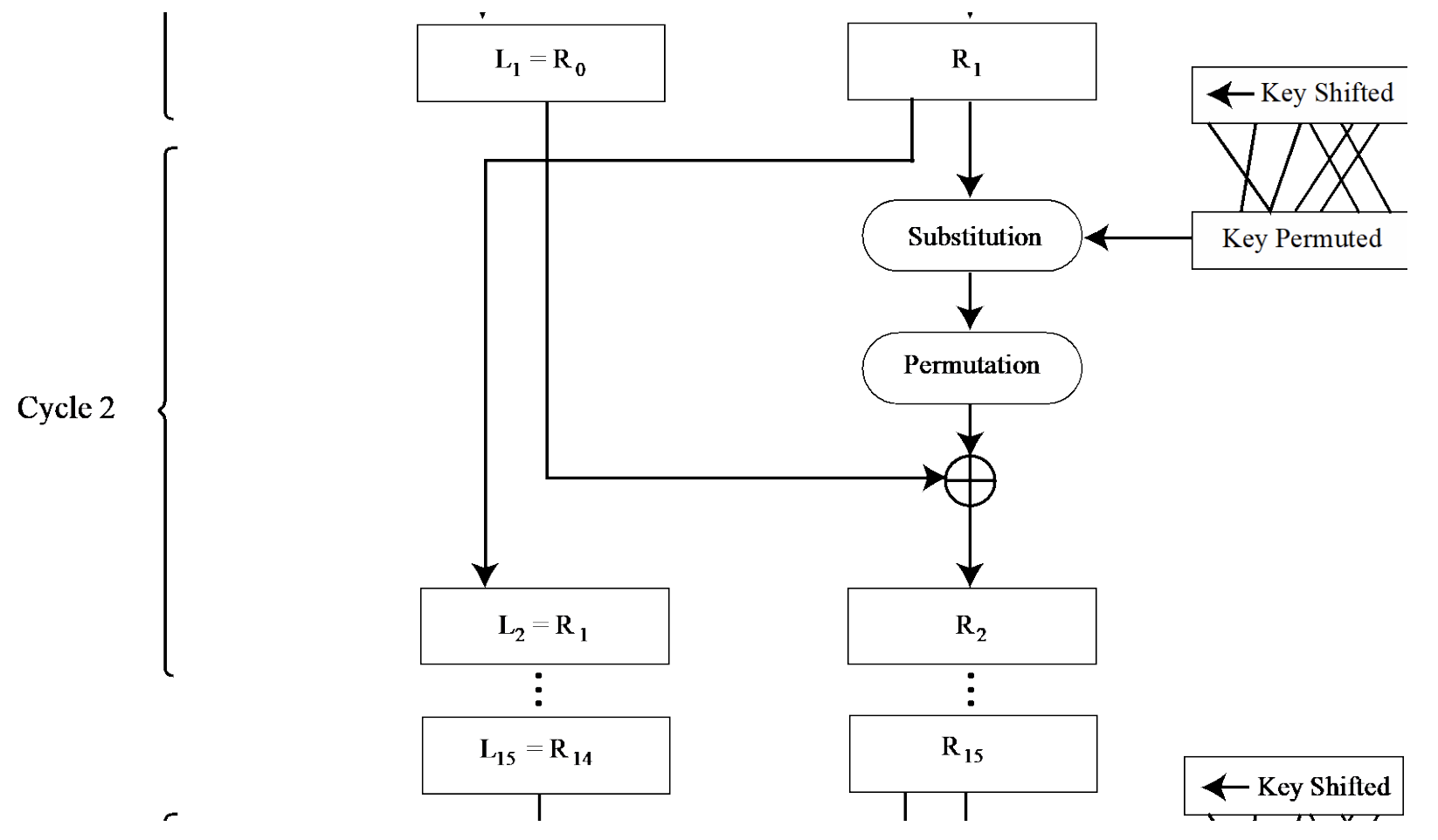
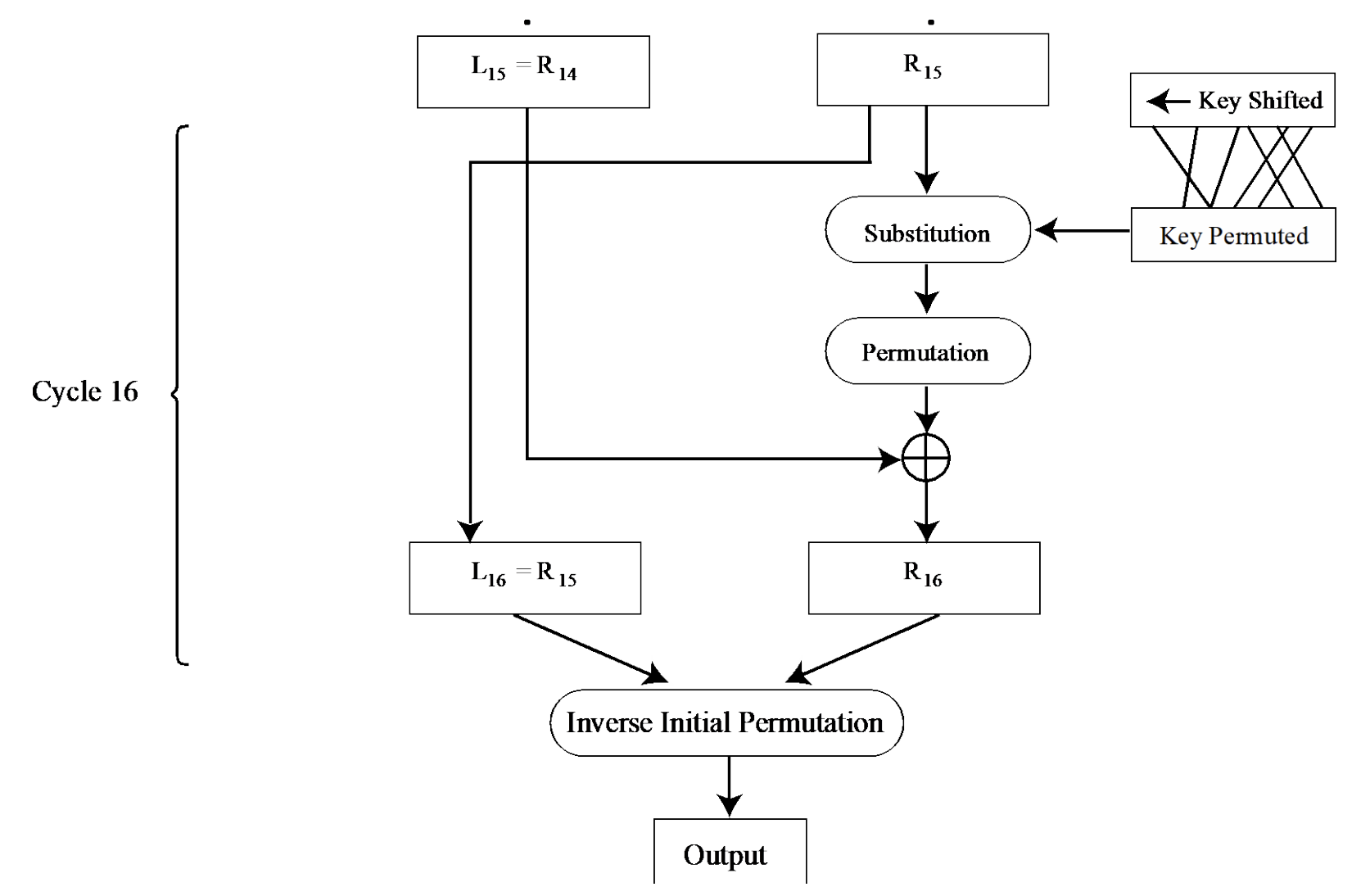
Substitution, Transposition 과정을 16번 반복하면 수가 random하게 보여서 암호화가 될 것이라고 기대한 알고리즘이다.
그러나 DES와 같은 블록 암호 방식은 과정을 반복하기 때문에 공격자에게 너무 많은 정보를 제공한다. 예를들어 DES는 64비트 블록을 동일한 방식으로 암호화하기 때문에 동일한 키로 동일한 블록을 암호화하면 동일한 암호문이 생성된다. 이는 공격자에게 패턴을 분석할 수 있는 단서를 제공하며, 메시지에 반복적으로 나타나는 공통된 시작이나 끝 부분이 노출될 가능성을 높인다. 또한, 동일한 키를 여러 트랜잭션에서 재사용할 경우 보안이 더 취약해질 수 있다.
체이닝은 이러한 문제를 해결하기 위해 각 블록의 암호화가 이전 블록의 암호문에 의존하도록 설계된 방식이다. 이를 통해 현재 블록의 암호문은 이전 블록의 암호문과 결합되어 계산되며, 동일한 블록이라도 항상 다른 암호문이 생성되도록 한다. 체이닝 방식은 암호화 데이터의 패턴 노출을 막아 보안을 강화하며, 대표적으로 Cipher Block Chaining(CBC) 방식이 사용된다.
CBC 방식에서는 첫 번째 블록이 초기화 벡터(IV)와 XOR 연산을 통해 결합된 후 암호화되고, 이후 각 블록은 이전 블록의 암호문과 XOR 연산으로 결합되어 암호화된다. 이로 인해 메시지의 암호화 과정이 서로 연결되며, 하나의 블록 암호화가 전체 암호화 결과에 영향을 미치게 된다. 체이닝은 데이터 암호화의 안전성을 높이고 공격자가 패턴을 분석할 수 있는 가능성을 줄이는 중요한 방법이다.
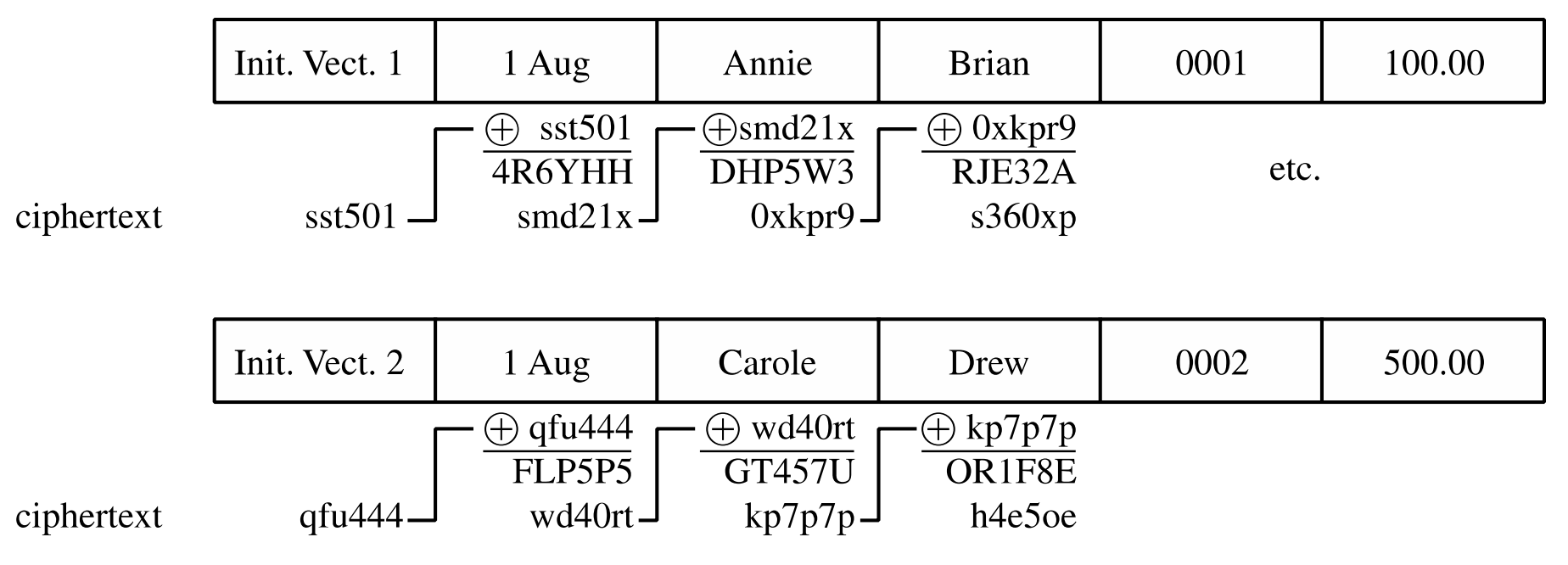
위와 같은 간단한 예시를 보면 패턴을 찾지 못하도록 하는 initial vector를 다르게 적용하고 앞의 값에 의존되도록 XOR를 연쇄적으로 적용하면 같은 단어라도 경우에 따라 다르게 암호화되는 것을 볼 수 있다.
AES
AES(Advanced Encryption Standard)는 라운드 기반의 대칭 블록 암호화 알고리즘으로 각 라운드는 다음의 주요 단계를 거친다.
- Byte Substitution (바이트 대체)
- AES는 S-Box(Substitution Box)를 사용하여 입력 데이터의 각 바이트를 대체한다.
- 이 과정은 암호화의 비선형성을 증가시키고 보안을 강화한다.
- S-Box는 미리 정의된 표에 따라 바이트 값을 다른 값으로 매핑한다.
- Shift Rows (행 이동)
- 데이터 블록의 각 행이 왼쪽으로 순환 이동(Shift)된다.
- 이동 거리는 행의 인덱스에 따라 다르다(첫 번째 행은 이동하지 않고, 두 번째 행은 1칸 이동 등).
- 이는 암호문의 혼합성을 높이고 패턴을 숨기기 위한 단계이다.
- Mix Columns (열 혼합)
- 데이터 블록의 각 열이 수학적 행렬 곱셈 연산을 통해 섞인다.
- 이 과정은 데이터를 확산(Diffusion)시키며, 평문과 암호문 간의 관계를 복잡하게 만든다.
- 마지막 라운드에서는 이 단계가 생략된다.
- Add Round Key (라운드 키 추가)
- 현재 상태(State)의 데이터와 라운드 키를 XOR 연산하여 결합한다.
- 라운드 키는 초기 키에서 생성되며, 라운드마다 다른 키가 사용된다.
- 이는 데이터와 키를 긴밀히 연결하여 보안을 강화한다.
- 다음 라운드 진행
- 위의 단계를 여러 라운드(128비트 키의 경우 10라운드) 반복한다.
- 각 라운드가 끝날 때마다 출력 데이터는 다음 라운드의 입력 데이터가 된다.
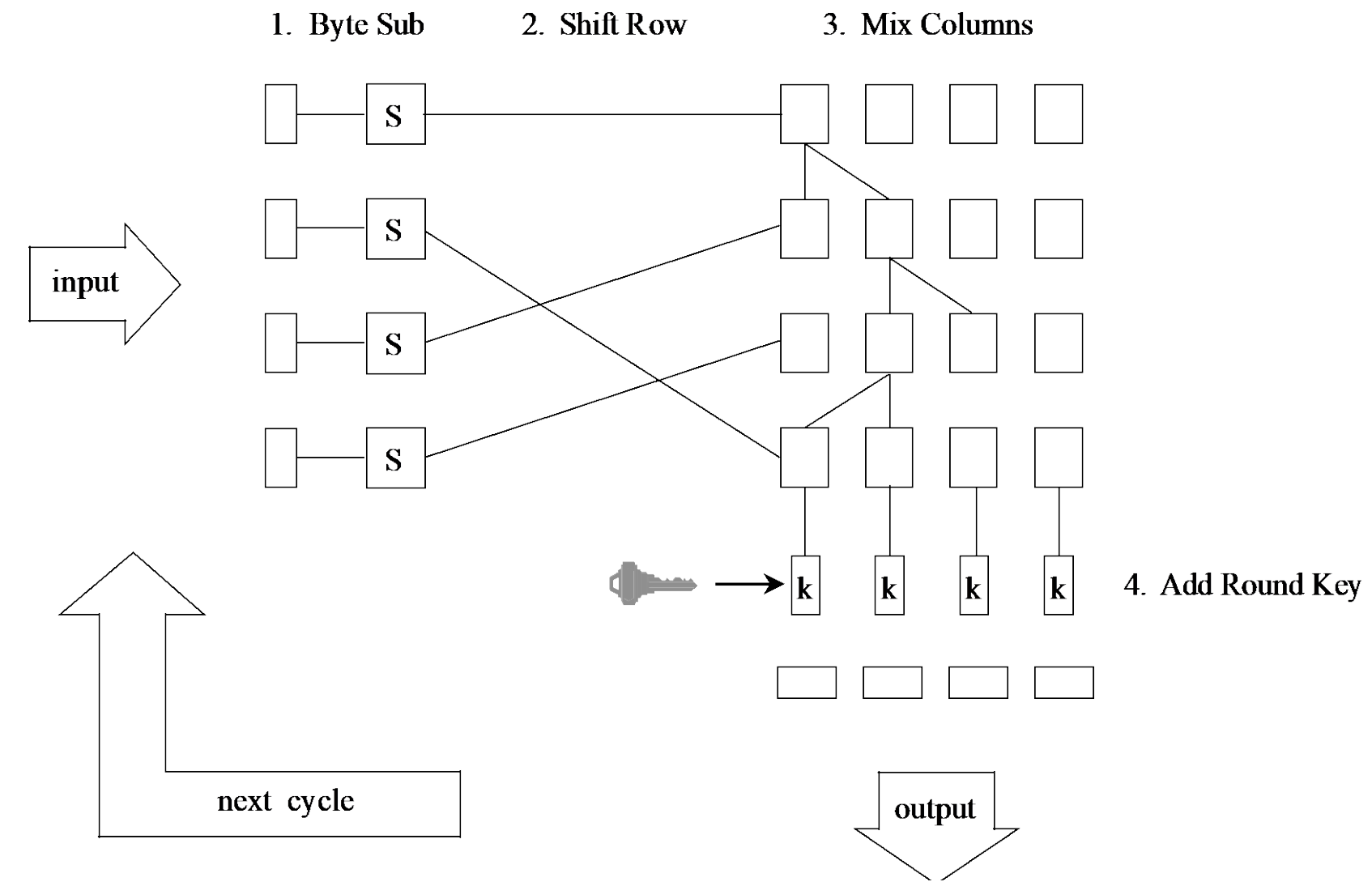
암호화 키는 128, 192, 256의 세 가지 중 하나가 될 수 있으며, 각각 AES-128, AES-192, AES-256으로 불린다. 암호화 키의 길이에 따라 실행하는 라운드의 수가 다른데, 각각 10, 12, 14 라운드를 실행한다.
S-Box를 간단히 설명하자면 입력 데이터를 지정된 숫자로 바꿔서 암호를 깨기 어렵게 만드는 기법이다. AES는 이걸 창조롭게 재발명하여 암호화 속도를 높이고 싶으면 S-Box를 메모리에 박아놓고, 프로그램 메모리 양을 줄이려면 실행시 S-Box를 연산으로 구해내는 기법을 사용했다.
- 출판 이후 광범위한 분석
- AES는 1997년에 처음 발표된 이후로 철저하고 광범위한 분석을 받아왔다.
- AES의 보안을 위협하는 주요 공격은 매우 전문적이고 이론적인 수준에 그쳤다.
- 구조적 강점
- AES는 명확한 기본 구조를 가지고 있어, 키 길이를 확장해야 하는 상황에서도 유사한 접근 방식을 사용할 수 있다.
- 예를 들어, 256비트 이상의 키를 사용해야 할 경우, AES의 기존 알고리즘을 약간 변형하여 확장할 수 있다.
- 현재까지 심각한 공격 없음
- 현재까지 AES의 전체적인 강점을 심각하게 의심하게 만든 공격은 발견되지 않았다.
- 이는 AES가 여전히 강력한 보안을 제공하는 암호화 알고리즘임을 입증한다.
AES는 높은 수준의 보안을 유지하면서도 하드웨어와 소프트웨어에서 효율적으로 구현할 수 있는 설계 덕분에, 대칭 키 암호화의 표준으로 자리 잡았다. AES는 오늘날 인터넷 보안, 데이터 암호화, 금융 시스템 등 다양한 분야에서 널리 사용되고 있다.
AES(Advanced Encryption Standard)는 1997년에 처음 발표된 이후로 현재까지 철저하고 광범위한 분석을 받아왔다. 이 과정에서 AES의 보안을 위협하는 주요 공격은 매우 전문적이고 이론적인 수준에 그쳤으며, 실제적으로 AES의 강점을 심각하게 위협한 공격은 발견되지 않았다. AES는 명확한 구조적 강점을 가지고 있어, 만약 256비트 이상의 긴 키를 필요로 하는 상황에서도 기존 알고리즘의 기본 틀을 유지하면서 약간의 변형을 통해 확장이 가능하다.
AES는 오늘날까지도 높은 수준의 보안을 제공하며, 데이터 암호화와 인터넷 보안, 금융 시스템과 같은 다양한 분야에서 널리 사용되고 있다. 현재까지 AES의 전체적인 강점에 대해 심각한 의문을 제기하는 공격이 없었기 때문에 AES는 여전히 대칭 키 암호화 알고리즘의 표준으로 자리 잡고 있다.
RSA
RSA는 1978년에 처음 도입된 이후 현재까지 광범위한 암호 해독 분석을 거쳤으며, 구조적 문제를 위협하는 심각한 결함은 발견되지 않았다. RSA는 큰 소수를 소인수분해하는 계산적 어려움에 기반을 둔 암호화 알고리즘으로, 소인수분해는 매우 복잡하고 현재 가장 빠른 알고리즘도 지수적으로 시간이 증가한다는 특성을 갖고 있다. RSA는 비대칭 암호화 방식으로, 공개 키와 개인 키라는 두 가지 키를 사용한다. 공개 키는 데이터를 암호화하는 데 사용되고, 개인 키는 이를 복호화하는 데 사용된다. 두 키는 서로 교환 가능하며, 특정 상황에 따라 개인 키를 암호화에 사용하고 공개 키를 복호화에 사용할 수도 있다.
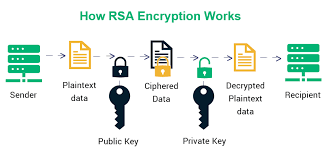
1. Key 생성

2. Encryption
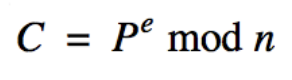
3. Decryption
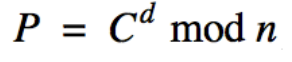
참고필기


Message Digest
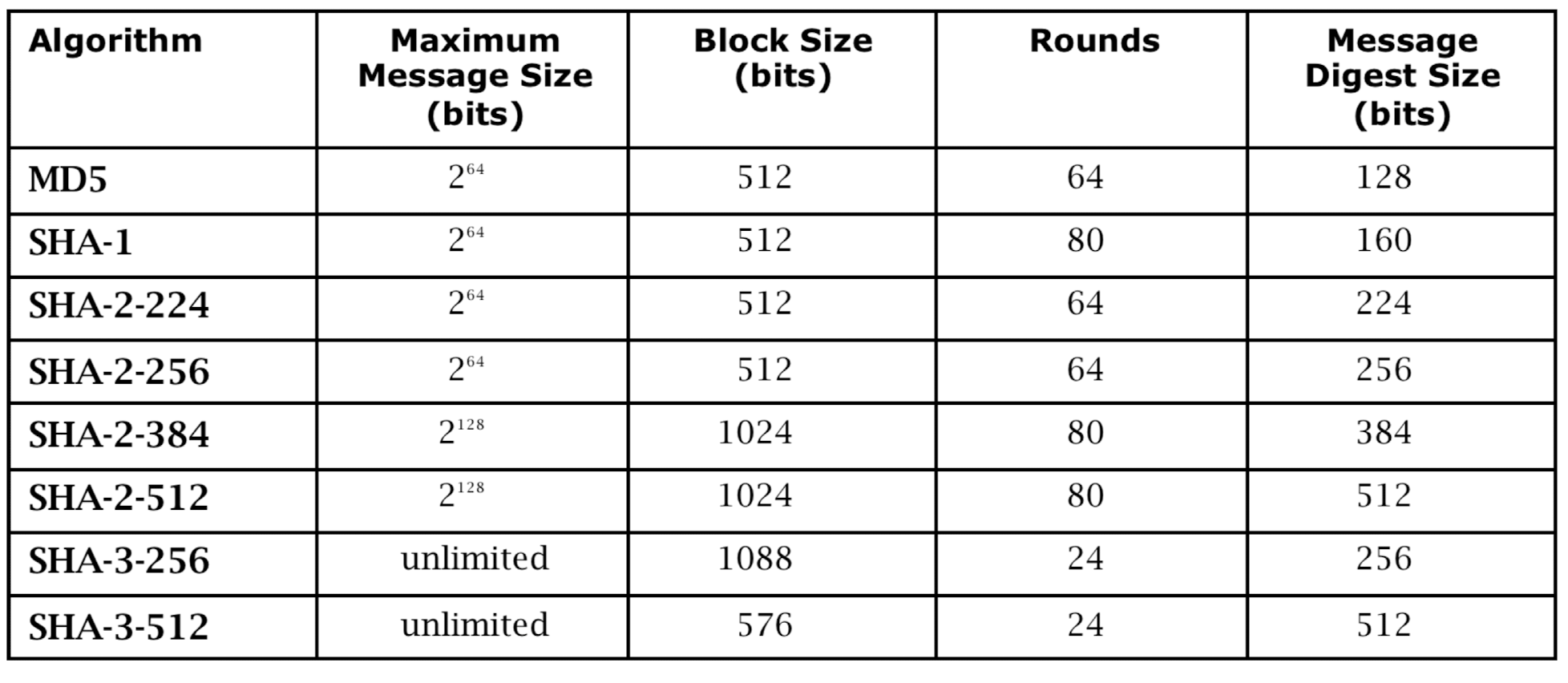
메시지 다이제스트(Message Digest)는 데이터 블록의 변경 여부를 탐지하기 위해 사용하는 암호학적 해시 함수이다. 이는 입력 데이터를 고정된 길이의 해시 값으로 변환하며, 주로 무결성 확인, 인증, 통신 프로토콜에서 사용된다. 메시지 다이제스트는 one-way hash function으로 작동한다. 일방향성은 입력 데이터를 해시 값으로 변환한 후 다시 원래의 데이터를 복구하는 것이 불가능하도록 설계되었다. 또한 collison resistance을 가져야 하며, 이는 두 개의 서로 다른 입력 데이터가 동일한 해시 값을 가지지 않도록 보장한다. 현대적인 해시 함수는 다음 두 가지 조건을 만족해야 한다.
첫째, 일방향성(one-way property)을 가져야 하며, 이는 해시 값에서 원래 입력 값을 유추하는 것이 불가능하도록 한다.
둘째, 명확한 충돌이 없어야 하며, 이는 동일한 해시 값을 생성하는 입력 쌍을 찾는 것이 실질적으로 불가능하다는 것을 의미한다.
메시지 다이제스트는 공개 키 암호화 알고리즘 및 디지털 서명과 함께 사용되며, 데이터 무결성 확인과 인증을 위한 핵심 기술로 자리 잡고 있다.
Digital Signature
디지털 서명(Digital Signature)은 데이터를 서명한 사람이 실제로 작성했음을 증명하고, 서명이 위조되지 않았음을 보장하는 기술이다. 디지털 서명은 다음 두 가지 필수 조건을 충족해야 한다.
- 위조 불가능(Unforgeable)
- 서명자의 개인 키 없이는 누구도 디지털 서명을 생성할 수 없어야 한다.
- 이는 서명이 다른 사람에 의해 생성될 수 없도록 보장한다.
- 검증 가능(Authentic)
- 서명을 받은 사람은 해당 서명이 실제로 서명자로부터 온 것임을 확인할 수 있어야 한다.
- 서명과 함께 제공된 공개 키를 사용해 이를 검증한다.
추가적으로 디지털 서명은 다음 두 가지를 만족하면 이상적이다.
- 변경 불가능(Not alterable)
- 서명이나 데이터가 변경되면 즉시 이를 감지할 수 있어야 한다.
- 이는 서명이 위조 또는 변조되지 않도록 보장한다.
- 재사용 불가능(Not reusable)
- 이전에 생성된 서명을 재사용하려는 시도를 서명을 받는 사람이 탐지할 수 있어야 한다.
- 이는 동일한 서명을 여러 번 악용할 가능성을 방지한다.
디지털 서명은 일반적으로 공개 키 암호화를 사용하여 생성된다. 서명자는 자신의 개인 키를 사용해 데이터에 서명 값을 계산한다. 이후, 데이터를 받은 사람은 서명자의 공개 키를 이용해 서명 값이 해당 개인 키로 생성되었음을 검증한다. 이를 통해 데이터의 무결성과 서명자의 신원을 동시에 보장할 수 있다.
Elliptic Curve Cryptosystems
타원 곡선 암호 시스템(ECC, Elliptic Curve Cryptosystems)은 RSA 알고리즘의 대안으로, 비대칭 암호화에 사용된다. RSA 알고리즘은 강력한 보안성을 제공하지만, 특허 문제로 인해 상업적 사용에서 제약이 있을 수 있다. ECC는 이러한 문제를 해결하며 두 가지 주요 장점을 제공한다.
- 공공 도메인
ECC의 일반 알고리즘은 공공 도메인에 속하므로, RSA와 달리 특허 문제가 없다. 그러나 일부 ECC 기술은 특허로 보호될 수 있다. - 짧은 키 길이
ECC는 RSA와 유사한 수준의 보안을 제공하면서도 더 짧은 키 길이를 사용할 수 있다. 이는 계산 효율성을 높이고, 저장 공간과 데이터 전송량을 줄이는 데 기여한다.
ECC는 특히 IoT 장치와 같이 자원이 제한된 환경에서 효율적인 암호화 솔루션으로 널리 사용되고 있다.
Quantum Cryptography
양자 암호화는 이렇게 가볍게 다룰 수 있는 내용이 아니다. 그냥 컨셉만 훑는다고 생각하자.
양자 암호(Quantum Cryptography)는 수학이 아닌 물리학에 기반하여 빛 입자인 광자(Photon)를 사용한 암호화 기술이다. 이는 전통적인 암호 방식의 한계를 극복하고, 높은 보안성을 제공할 수 있는 대안으로 주목받고 있다.
양자 암호는 광자의 특정 물리적 특성을 측정하고 하이젠베르크의 불확정성 원리를 활용한다. 이러한 원리로 인해 송신자와 수신자는 통신 중 도청자를 쉽게 탐지할 수 있다. 이는 도청자가 광자의 상태를 관찰하면 그 자체로 상태가 변경되어 이를 감지할 수 있기 때문이다.
현재 양자 암호 기술은 초기 프로토타입 단계에 머물러 있다. 실질적으로 사용 가능한 광자 총(Photon Gun) 및 수신기를 제작하는 것은 기술적으로 매우 어려운 과제이다. 하지만, 향후 10년 이내에 양자 암호 기술이 실용화될 가능성이 있으며, 기존 암호화 시스템에 비해 암호화 통신의 보안을 크게 개선할 것으로 기대된다.

Post-Quantum Cryptography
양자내성암호(Post Quantum Cryptography; PQC)는 양자컴퓨터로도 풀어내는 데 수십억 년이 걸리는 복잡한 수학 알고리즘을 사용하는 암호화 방식이다. '양자컴퓨터' 시대에는 기존 암호체계가 취약할 수 있어 새로운 보안기술을 확보하는 게 필수다.
특징을 살펴보자면 다음과 같다. 1.수학에 기반을 둔다. 2. 양자 컴퓨터 등장 이후에도 안전한 암호화 알고리즘이다. 3. 고전적 계산 위협과 양자 계산 위협 모두에 효과적이다. 4. 특수 장비 없이 기존 하드웨어에서 작동한다. 5. 현재 활발한 표준화 작업이 진행 중이다.
'Quality control (Univ. Study) > Information Security' 카테고리의 다른 글
| Buffer-overflow attack lab (4) (0) | 2024.12.08 |
|---|---|
| Cloud Computing (0) | 2024.12.08 |
| Privacy (2) | 2024.12.07 |
| Buffer-overflow attack lab (3) (0) | 2024.12.07 |
| Network security (2) | 2024.12.06 |


