B-Tree
Bayer & McCreight가 1970년에 제안한 구조이다. 차수 m인 B-트리의 특성은 아래와 같다.
1. B-트리는 공백이거나 높이가 1 이상인 m-원 탐색 트리이다.
2. 루트와 리프를 제외한 내부 노드는 아래와 같이 최소 e[m/2u] , 최대 m개의 서브트리를 갖고 있고 적어도 [m/2] - 1개의 키 값(노드의 반 이상 채워짐)을 갖고 있다.
3. 루트 : 리프가 아니면 적어도 두 개의 서브트리를 가진다.
4. 모든 리프는 같은 레벨이다.
또한 B-트리의 장점은 삽입,삭제 뒤에도 균형 상태 유지가 되고 저장 장치의 효율성이 좋다. 각 노드의 반 이상 키 값 저장을 저장하고 최악의 경우에도 O(log_n (N+1))의 시간복잡도를 보장한다.
아래는 이러한 특징이 반영된 3차 B-tree구조이다.

Insert
위의 B-트리 예시에 새로운 키 값 22, 41, 59, 57, 54, 44, 75, 124, 122, 123을 삽입해보며 그 방법을 확인해보자.



나머지 키 값인 33, 75, 124, 122를 차례로 삽입하는 과정에서는 문제가 발생하지 않고 마지막 키 값인 123을 삽입하고나면 B-트리는 아래와 같이 한 레벨 증가된다.

Found = false;
read root;
do {
N = number of keys in current node;
if (n-key == key in current node) found = true;
else if (ln-key < key1) P = P0;
else if (ln-key > keyN) P = PN;
else P = Pi-1; /* for some i where keyi-1 < ln-key < keyi; */
if (P != null) {
push onto stack address of current node;
read node pointed to by P;
}
} while (!Found && P is not null);
if (Found) report ln-key already in tree;
else { /* ln-key를 B-tree에 삽입한다 */
P = nil;
Finished = false;
do {
if (current node is not full) {
put ln-key in current node;
/* 노드 안에 키 수를 유지하도록 키를 정렬한다 */
Finished = true;
} else {
copy current node to TOO BIG;
insert ln-key and P into TOO BIG;
ln-key = center key of TOO BIG;
current node = 1st half of TOO BIG;
get space for new node, assign address to P;
new node = 2nd half of TOO BIG;
if (stack not empty) {
pop top of stack;
read node pointed to;
} else { /* 트리의 레벨이 하나 증가한다. */
get space for new node;
new node = pointer to old root, ln-key and P;
Finished = true;
}
}
} while (!Finished);
}Delete
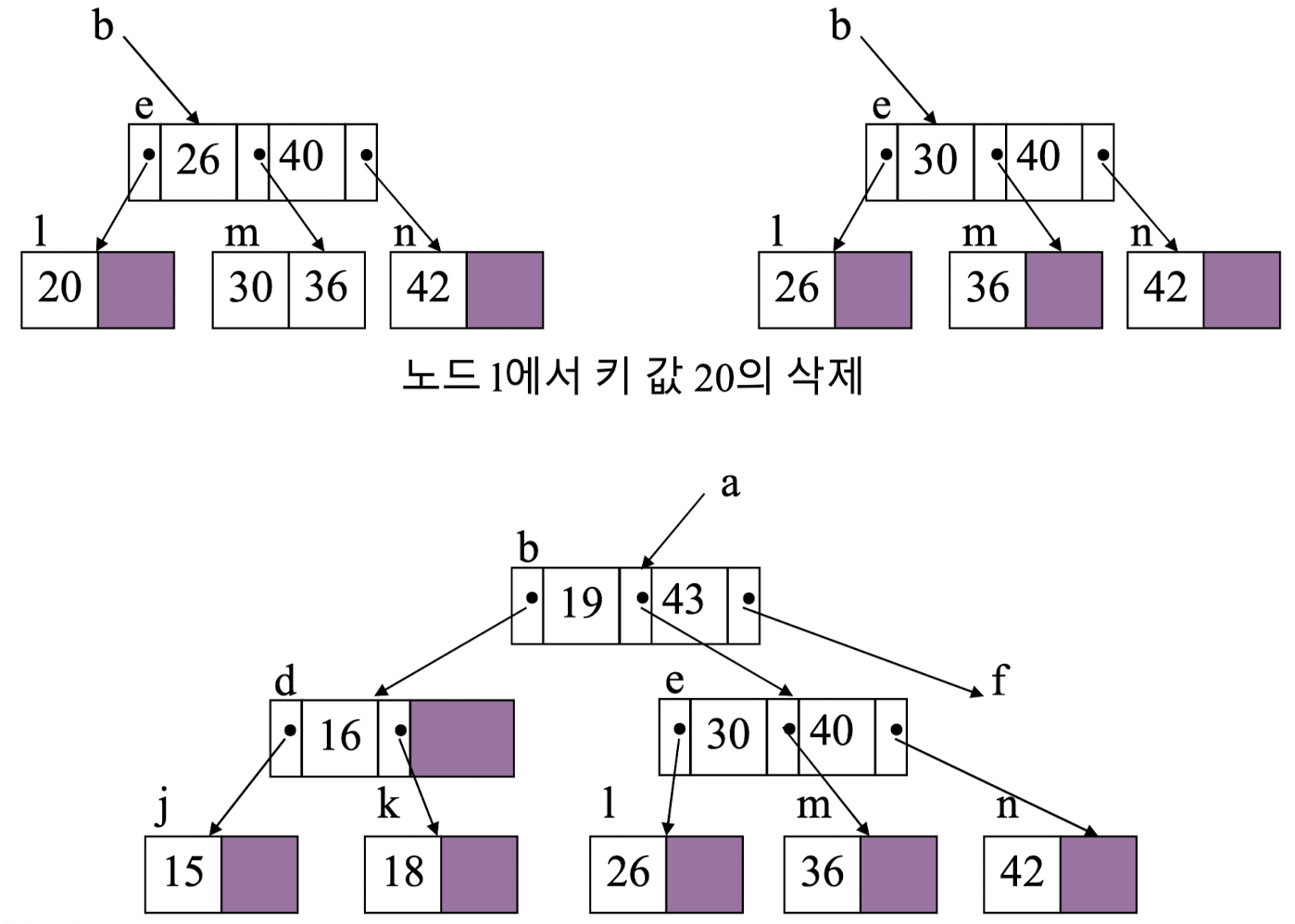
삭제될 키 값이 내부노드에 있는 경우 이 키 값의 후행 키 값과 교환 후 리프 노드에서 삭제한다. 리프 노드에서의 삭제 연산이 더 간단하다. 후행 키 값 대신 선행 키 값을 사용할 수 있다.
최소 키 값 수( [m/2] - 1)보다 작은 경우에는 underflow가 발생한다. 이때 두가지 정도의 경우가 있다.
- 재분배(redistribution)
최소 키 값보다 많은 키를 가진 형제 노드에서 차출한다.
부모 노드에 있던 키 값을 해당 노드로 이동키 빈자리에 차출된 형제 노드의 키 값을 이동시킨다.
트리 구조를 변경시키지 않는다.
- 합병(merge)
재분배가 불가능한 경우에 적용한다.
형제 노드와 합치는 방법으로, 합병 결과 빈 노드는 제거한다.
트리 구조가 변경된다.
삭제 과정을 예시를 통해 살펴보자.


search tree for Out-key forming stack of node addresses;
if (Out-key is not in terminal node) {
search for successor key of Out-key at terminal level (stacking node addresses);
copy successor over Out-key;
terminal node successor now becomes the Out-key;
}
/* 키를 삭제하고 트리를 재조정한다. */
Finished = false;
do {
remove Out-key
if (current node is root or is not too small)
Finished = true;
else if (redistribution possible) {
/* A-sibling > minimum이 상실한 때 재배분 가능 */
/* 재배분 실행 */
copy "best" A-sibling, intermediate parent key, and current (too-small) node into TWOBNODE;
copy keys and pointers from TWOBNODE to "best" A-sibling, parent, and current node so A-sibling and current node are roughly equal size;
Finished = true;
} else { /* 적당한 A-sibling과 통합한다 */
choose best A-sibling to concatenate with;
put in the leftmost of the current node and A-sibling the contents of both nodes and the intermediate key from the parent;
discard rightmost of the two nodes;
intermediate key in parent now becomes Out-key;
}
} while (!Finished);
if (no keys in root) {
/* 트리의 레벨이 하나 감소한다 */
new root is the node pointed to by the current root;
discard old root;
}B+Tree
B+Tree는 Knuth가 제안한 B-Tree의 또 다른 변형구조이다. Index set와 Sequence set로 구성되어 있고 B-트리의 약점이었던 순차 탐색의 성능 향상을 보완하기 위해 고안되었다. 이때 인덱스 세트(index set)는 리프 이외의 노드를 이야기하는 것이다. 키값만 존재하며 리프 노드에 대한 경로만 제공하는 구조를 갖고 있다. 순차 세트(sequence set)는 리프 노드를 이야기 하는 것이고 키값, 데이타 레코드의 주소들이 존재하는 구조를 갖고 있다.

현재 DBMS와 OS의 인덱스 기준이 되기도 하는 구조이다. 단점을 보자면 인덱스 세트에 저장 되어있는 값을 순차 세트에 중복 저장해야하기 때문에 공간 낭비가 심하다. 또한 find하는 경우 반드시 leaf까지 가서 찾아봐야해서 탐색시간이 오래걸린다. 또 다른 특징들을 살펴보자.
1. 루트는 0 또는 2에서 m개 사이의 서브트리를 가진다.
2. 루트와 리프를 제외한 모든 내부 노드는 최소 [m/2]개, 최대 m개의 서브트리를 갖는다.
3. 리프가 아닌 노드에 있는 키 값의 수는 그 노드의 서브트리 수보다 하나 적다.
4. 모든 리프 노드는 같은 레벨에 존재한다.
5. 한 노드 안에 있는 키 값들은 오름차순으로 정렬한다.
6. 리프 노드는 모두 링크로 연결되어 있다.
Insert
B-트리의 리프 노드에 삽입하는 것과 유사하다. 차이는 분할시 중간 키값(분할된 왼쪽 노드에서 제일 큰 키값)의 복사본이 부모
인덱스 노드로 올라가 저장된다는 것이다. 인덱스 노드 분할 시에는 B-트리와 똑같은 알고리즘을 수행하고, 중간 키는 부모 노드로 올라간다.
15, 69, 110이 있는데 90을 삽입하면 아래와 같이 정렬된다.

20, 120을 삽입하면 아래와 같고

이어서 40을 삽입하고

마지막으로 125를 삽입하면 아래의 결과가 나온다.

Delete
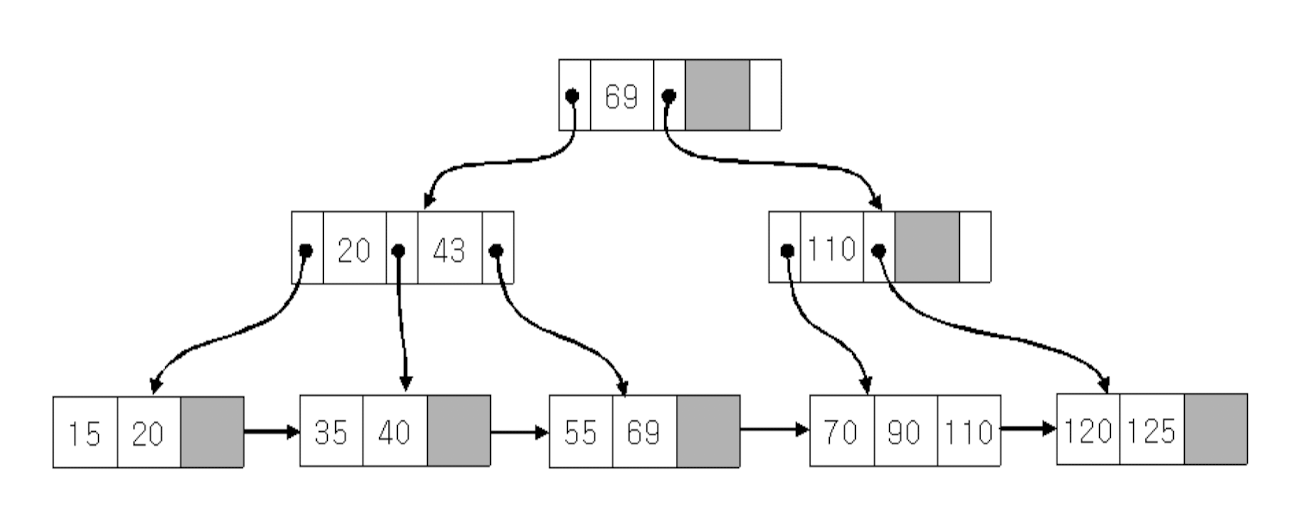
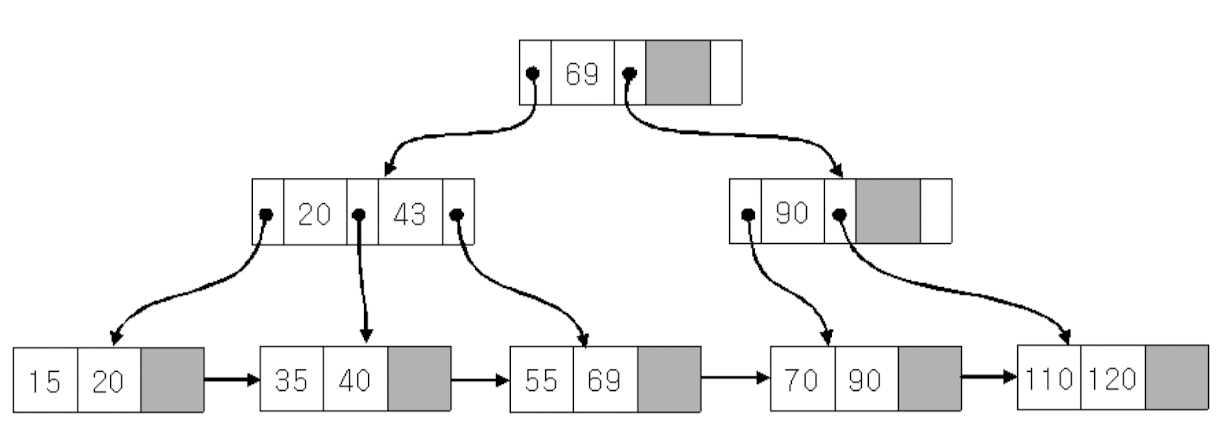
삭제 과정도 B-트리와 유사하나 키값의 삭제는 리프 노드에서만 수행한다는 차이가 있다. 인덱스 세트의 키 값을 삭제할 필요가 있는 경우에는 삭제하지 않고 분리자(separator)로 이용한다.
아래는 43, 125, 55를 순서대로 하나씩 삭제하는 과정이다.


'Univ. Study > Algorithm Design' 카테고리의 다른 글
| Algorithm Design - 라빈-카프 / 패턴 매칭 (0) | 2024.04.17 |
|---|---|
| Algorithm Design - 스트링 탐색 알고리즘(Naïve/KMP/BM) (0) | 2024.04.12 |
| Algorithm Design - Tree (0) | 2024.04.04 |
| 알고리즘 설계 실습 - 트리 순환 (1) | 2024.04.03 |
| 알고리즘 설계 실습 - k번째 교환(heap sort) (0) | 2024.03.30 |



