상호정보량
단어의 동시발생 행렬에는 개선할 점들이 있다. 왜냐하면 발생횟수라는 것은 그리 좋은 특징이 아니기 때문이다. 예를들어 "the"와 "car"의 동시발생을 생각해보면 두 단어의 동시발생 횟수는 아주 많을 것이다. 이때 "car"와 "drive"는 관련이 깊은데도 불구하고, 단순히 등장 횟수만을 본다면 "car"는 "drive"보다 "the"와의 관련성이 훨씬 강하다고 나올 것이다. "the"가 고빈도 단어라서 "car"와 강한 관련성을 갖는다고 평가되기 때문이다. 이 문제를 해결하기 위해 점별 상호정보량(PMI; Pointwise Mutual Information)이라는 척도를 사용한다.

이를 이용하여 단어 수 10,000개의 말뭉치가 있다고 할 때 "the", "car", "drice"가 각각 1,000번, 20번, 10번 나타났다고 할때 간의 관계성을 살펴보면 아래와 같이 계산된다.
PMI("the","car")=2.32
PMI("car","drive")=7.97
위 결과처럼 PMI를 이용하면 "car"는 "the"보다 "drive"의 연관성이 높다는 결과가 나오는 것을 확인할 수 있다. 이때 PMI는 두단어의 연관성이 0이면 log연산의 결과가 log₂0 = -∞이 된다는 문제가 있어서 PPMI(Positive PMI)를 사용한다.

PPMI는 PMI가 음수일때 0으로 취급하기 때문에 -∞ 문제를 해결할 수 있다.
def ppmi(C, verbose=False, eps=1e-8):
M = np.zeros_like(C, dtype=np.float32)
N = np.sum(C)
S = np.sum(C, axis=0)
total = C.shape[0] * C.shape[1]
cnt = 0
for i in range(C.shape[0]):
for j in range(C.shape[1]):
pmi = np.log2(C[i, j] * N / (S[j]*S[i]) + eps)
M[i, j] = max(0, pmi)
if verbose:
cnt += 1
if cnt % (total//100 + 1) == 0:
print('%.1f%% 완료' % (100*cnt/total))
return M이때 인수 C는 동시발생 행렬, verbose는 진행상황 출력 여부를 결정하는 플래그이다.
이번엔 동시발생 행렬을 PPMI행렬로 변환해보려한다.
import sys
sys.path.append('..')
import numpy as np
from common.util import preprocess, create_co_matrix, cos_similarity, ppmi
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
C = create_co_matrix(corpus, vocab_size)
W = ppmi(C)
np.set_printoptions(precision=3) # 유효 자릿수를 세 자리로 표시
print('동시발생 행렬')
print(C)
print('-'*50)
print('PPMI')
print(W)
"""
동시발생 행렬
[[0 1 0 0 0 0 0]
[1 0 1 0 1 1 0]
[0 1 0 1 0 0 0]
[0 0 1 0 1 0 0]
[0 1 0 1 0 0 0]
[0 1 0 0 0 0 1]
[0 0 0 0 0 1 0]]
--------------------------------------------------
PPMI
[[ 0. 1.807 0. 0. 0. 0. 0. ]
[ 1.807 0. 0.807 0. 0.807 0.807 0. ]
[ 0. 0.807 0. 1.807 0. 0. 0. ]
[ 0. 0. 1.807 0. 1.807 0. 0. ]
[ 0. 0.807 0. 1.807 0. 0. 0. ]
[ 0. 0.807 0. 0. 0. 0. 2.807]
[ 0. 0. 0. 0. 0. 2.807 0. ]]
"""PPMI 행렬에도 여전히 문제가 있다. 말뭉치의 어휘 수가 증가함에 따라 벡터의 차원 수도 증가한다. 예를 들어 말뭉치의 어휘 수가 10만 개라면 그 벡터의 차원 수도 똑같이 10만이 되는 것이다. 10만 차원의 벡터를 다루는 것은 비현실적이다. 또한 원소 대부분이 0이어서 벡터의 원소 대부분이 중요하지 않다. 이런 벡터는 노이즈에 약하고 견고하지 못하기 때문에 벡터의 차원 감소로 이러한 문제들을 해결한다.
차원감소
차원감소(dimensionality reduction)는 문자 그대로 벡터의 차원을 줄이는 방법인데 이때 중요한 정보는 최대한 유지하면서 줄이는 게 핵심이다.

위는 직관적인 예로 데이터의 분포를 고려해 중요한 '축'을 찾는 일을 수행한다. 2차원 데이터를 1차원으로 표하기 위한 적합한 축을 찾아내어 1차원으로 차원 축소를 시킨 것을 볼 수 있다. 차원을 감소시키는 방법은 다양하지만 대표적인 방법중 하나인 특잇값분해(SVD, Singular Value Decomposition)를 이용하고자 한다. SVD는 임의의 행렬 세개의 곱으로 분해하고 수식은 아래와 같다.

여기서 U와 V는 직교행렬이고, 그 열벡터는 서로 직교한다. 또한 S는 대각행렬이다.

U는 '단어 공간'으로 취급할 수 있고 대각 행렬인 S는 '특잇값'을 의미한다. 따라서 아래와 같이 중요도가 낮은 원소(특잇값이 낮은 원소)를 깎아내는 방법을 이용할 수 있다.

이를 단어의 PPMI 행렬에 적용하면 '행렬 X의 각 행에는 해당 단어 ID의 단어 벡터가 저장되어 있으며, 그 단어 벡터가 행렬 U'라는 차원 감소된 벡터로 표현되는 것이다.
SVD에 의한 차원 감소
SVD를 파이썬 코드로 살펴보자. 선형대수를 뜻하는 "linalg"라는 넘파이의 모듈이 제공하는 svd 메서드를 이용하면된다.
import sys
sys.path.append('..')
import numpy as np
import matplotlib.pyplot as plt
from common.util import preprocess, create_co_matrix, ppmi
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(id_to_word)
C = create_co_matrix(corpus, vocab_size, window_size=1)
W = ppmi(C)
# SVD
U, S, V = np.linalg.svd(W)단어 ID가 0인 단어 벡터를 변환해보자.
print(C[0] # 동시발생 행렬
# [0 1 0 0 0 0 0]
print(W[0]) # PPMI 행렬
# [ 0. 1.807 0. 0. 0. 0. 0. ]
print(U[0]) # SVD
# [ 3.409e-01 -1.110e-16 -1.205e-01 -4.441e-16 0.000e+00 -9.323e-01 2.226e-16]이 결과에서 보듯 원래 희소벡터인 W[0]가 SVD에 의해서 밀집 벡터 U[0]으로 변화시켰다. 이제 2차원 벡터로 줄이고 싶으면 첫 두 원소를 선택하여 남기면된다.
print(U[0, :2])
# [ 3.409e-01 -1.110e-16]이를 그래프로 그려보면 아래와 같이 진행하면된다.
for word, word_id in word_to_id.items():
plt.annotate(word, (U[word_id, 0], U[word_id, 1]))
plt.scatter(U[:,0], U[:,1], alpha=0.5)
plt.show()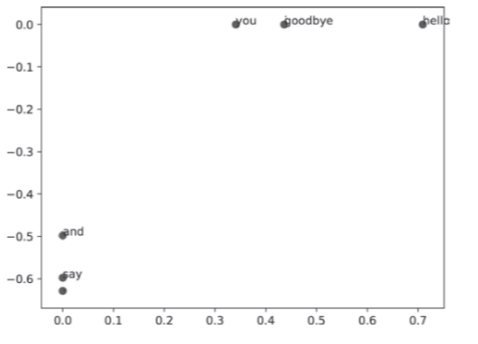
위 그래프에서 i와 goodbye가 겹쳐있다. 한문장만 이용했기에 만족스러운 결론을 얻기는 어렵다.
펜 트리뱅크(PTB) 데이터셋을 이용하여 테스트를 해보도록하자.
import sys
sys.path.append('..')
import numpy as np
from common.util import most_similar, create_co_matrix, ppmi
from dataset import ptb
corpus, word_to_id, id_to_word = ptb.load_data('train')
vocab_size = len(word_to_id)
print('동시발생 수 계산...')
C = create_co_matrix(corpus, vocab_size, window_size)
print('PPMI 계산...')
W = ppmi(C, verbose=True)
print('SVD 게산...')
try:
# truncated SVD (빠름!)
from sklearn.utils.extmath import randomized_svd
U, S, V = randomized_svd(W, n_components=wordvec_size, n_iter=5, random_state=None)
except ImportError:
# SVD (느리고 메모리 훨씬 많이 사용!)
U, s, V = np.linalg.svd(W)
word_vecs = U[:, wordvec_size]
querys = ['you', 'year', 'car', 'toyota']
for query in querys:
most_similar(query, word_to_id, id_to_word, word_vecs, top=5)SVD를 수행하는 데 sklearn의 randomized_svd() 메서드를 이용했다. 이 메서드는 무작위 수를 사용한 Truncated SVD로, 특잇값이 큰 것들만 계산하여 기본적인 SVD보다 훨씬 빠르다.
"""
[query] you
i: 0.702039909619
we: 0.699448543998
've: 0.554828709147
do: 0.534370693098
else: 0.512044146526
[query] year
month: 0.731561990308
quarter: 0.658233992457
last: 0.622425716735
earlier: 0.607752074689
next: 0.601592506413
[query] car
luxury: 0.620933665528
auto: 0.615559874277
cars: 0.569818364381
vehicle: 0.498166879744
corsica: 0.472616831915
[query] toyota
motor: 0.738666107068
nissan: 0.677577542584
motors: 0.647163210589
honda: 0.628862370943
lexus: 0.604740429865
"""위 결과를 보면 입력된 단어와 유사한 단어들을 잘 찾아낸 것을 볼 수 있다.
'Robotics & AI > DeepLearning' 카테고리의 다른 글
| 딥러닝 직접 구현하기 - (word2vec) (0) | 2024.02.01 |
|---|---|
| 딥러닝 직접 구현하기 - (추론 기반 기법) (0) | 2024.02.01 |
| 딥러닝 직접 구현하기 - (자연어처리) (1) | 2024.01.28 |
| Udemy - 딥러닝의 모든 것(AutoEncoder구축하기) (0) | 2024.01.24 |
| 딥러닝 직접 구현하기 - (CNN) (4) | 2024.01.19 |



