자연어처리
자연어처리는 흔히 NLP라고 불리는 Natural Language Processing을 의미한다. 이는 말그대로 인간이 사용하는 말을 컴퓨터가 이해하고 처리하기 위한 기술이다. 컴퓨터가 이해할 수 있는 프로그래밍 언어가 아닌 인간들이 사용하는 영어, 한글과 같은 자연어를 이해할 수 있도록 하는 것이다. 이때 말은 '문자'로 구성되어있고 말의 의미는 '단어'로 인해 만들어진다. 따라서 컴퓨터가 '단어의 의미만 이해하면 인간의 '말'을 이해할 수 있을 것이다. 따라서 이런 '단어의 의미'를 컴퓨터에게 파악시키는 것은 자연어처리에서 굉장히 핵심적인 부분이다.
Thesaurus
Thesaurus는 단어의 의미를 정의를 통해 설명하여 이해하는 방식과는 다르게 동의어나 유의어를 통해 단어의 의미를 알아가는 방식을 말한다. 예를 들어 car라는 단어를 이해하기 위해 car = auto, automobile, machine, motocar과 같이 정보를 기록하는 것이다. 또한 아래와 같이 단어의 상하위 개념, 전체와 부분과 같은 세세한 개념을 정의해두기도 한다.

가장 유명한 시소러스는 WordNet이다. 이는 프린스턴 대학에서 1985년부터 구축하기 시작한 전통있는 시소러스이다.
다만 시소러스는 치명적인 문제가 존재한다.
- 시대 변화에 대응하기 어렵다. (백투더퓨처에는 미래에서 온 마티가 과거의 박사에게 심각하단 의미로 heavy라는 단어를 이용하지만 박사는 heavy를 무겁다는 뜻으로만 이해한다.)
- 엄청난 인적 비용이 든다. (현존하는 영어 단어의 수는 1,000만 개가 넘으며 WordNet에 등록된 단어는 20만 개 이상이다.)
- 단어의 미묘한 차이를 표현할 수 없다. (가령, 빈티지와 레트로의 의미는 같으나 용법의 차이가 존재한다.)
위의 문제들을 해결하기 위해 '통계 기반 기법'과 신경망을 사용한 '추론 기반 기법'을 이용해보도록 하겠다.
통계 기반 기법
통계 기반 기법은 기본적으로 말뭉치(corpus)를 이용한다. 말뭉치는 대양의 텍스트 데이터이다. 다만 NLP를 염두에 두고 수집하고 정리한 텍스트 뎅터를 일반적으로 말뭉치라고 한다. 말뭉치의 문장들은 사람이 쓴 글이기 때문에 자연어에 대한 사람의 '지식'이 충분히 담겨 있다고 볼 수 있다.
먼저 모든 문자를 소문자로 변경한 이후 공백을 기준으로 분리하여 문장에 사용된 단어 목록을 만들어보자.
text = 'You say goodbye and I say hello.'
text = text.lower() # 모두 소문자로 변경
text = text.replace('.', ' .')
print(text) # you say goodbye and i say hello .
words = text.split(' ')
print(words) # ['you', 'say', 'goodbye', 'and', 'i', 'say', 'hello', '.']단어들에 ID를 부여하고, ID의 리스트로 이용할 수 있도록 만든다. 이를 통해 ID로 단어를 호출 할 수 있고, 단어로 ID를 호출할 수도 있다.
word_to_id = {}
id_to_word = {}
for word in words
if word not in word_to_id
new_id = len(word_to_id)
word_to_id[word] = new_id
id_to_word[new_id] = word
print(word_to_id) # {'you' 0, 'say' 1, 'goodbye' 2, 'and' 3, 'i' 4, 'hello' 5, '.' 6}
print(id_to_word) # {0 'you', 1 'say', 2 'goodbye', 3 'and', 4 'i', 5 'hello', 6 '.'}위에서 사용한 문장을 ID를 이용해 나타내보자.
corpus = [word_to_id[w] for w in words]
corpus = np.array(corpus)
print(corpus) # [0 1 2 3 4 1 5 6]위의 모든 기능을 모아 문장을 전처리하는 함수를 만들어보자.
def preprocess(text)
text = text.lower()
text = text.replace('.', ' .')
words = text.split(' ')
word_to_id = {}
id_to_word = {}
for word in words
if word not in word_to_id
new_id = len(word_to_id)
word_to_id[word] = new_id
id_to_word[new_id] = word
corpus = np.array([word_to_id[word] for word in words])
return corpus, word_to_id, id_to_word
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)전처리를 통해 단어 ID 목록(corpus), word_to_id 사전, id_to_word 사전을 얻을 수 있다.
단어의 분산 표현
색은 R, G, B로 구성할 수 있다. 이렇게 벡터표현으로 변경을 하면 적은 숫자로 많은 조합을 만들 수 있다. 단어도 벡터표현으로 변경할 수 있을까 벡터표현을 자연어처리 분야에서는 단어의 분산 표현(distributional representation)이라고 한다.
분산 표현은 단어를 벡터로 표현할 때 ‘단어의 의미는 주변 단어에 의해 형성된다’는 아이디어로부터 시작한다. 이 아이디어를 분포 가설(distributional hypothesis)이라고 한다. 분포 가설이 말하는 것은 단어 자체에는 의미가 없고, 그 단어가 사용된 맥락이 의미를 형성한다는 것이다. 예를 들어 drink라는 단어 근처에는 음료가 등장하기 쉽다. guzzle 이라는 단어 근처에도 음료가 잘 등장한다. 여기서 guzzle과 drink는 가까운 의미의 단어라는 것도 알 수 있다.
여기서는 맥락이라는 말을 사용하는데, 특정 단어 근처의 여러 단어를 맥락이라고 한다.

위 그림처럼 맥락이란 특정 단어를 중심에 둔 그 주변 단어를 말한다. 또한 맥락의 크리를 window size라고 한다.
동시발생 행렬
간단하게 맥락을 이용하는 방법은 그 주변에 어떤 단어가 몇 번이나 등장하는지를 세어 집계하는 방법이다. 이를 이 책에서는 ‘통계 기반’ 기법이라고 한다. 예시로 든 문장에서는 윈도우 크기가 1인 맥락에서 아래표처럼 주변 단어의 빈도를 얻을 수 있다. 이표를 동시발생행렬(co-occurrence matrix)라고 한다.
import sys
sys.path.append('..')
import numpy as np
from common.util import preprocess
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
print(corpus)
#[0 1 2 3 4 1 5 6]
print(id_to_word)
#[0:'you', 1:'say', 2:'goodbye', 3:'and, 4:'i', 5:'hello', 6:'.']
위는 모든 단어에 대한 동시발생 행렬이다. 말뭉치로부터 동시발생 행렬을 만들어주는 함수를 구현해보자.
def create_co_matrix(corpus, vocab_size, window_size=1)
corpus_size = len(corpus)
co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)
for idx, word_id in enumerate(corpus)
for i in range(1, window_size + 1)
left_idx = idx - i
right_idx = idx + i
if left_idx = 0
left_word_id = corpus[left_idx]
co_matrix[word_id, left_word_id] += 1
if right_idx corpus_size
right_word_id = corpus[right_idx]
co_matrix[word_id, right_word_id] += 1
return co_matrix위 함수에서 co_matrix를 0으로 채워진 2차원 배열로 초기화를 한다. 그다음 말뭉치의 모든 단어 각각에 대하여 정해진 윈도우 크기에 따라 주변 단어를 세고 이떄 말뭉치의 양쪽 끝을 넘지 않도록 확인도 한다. 이 함수는 동시발생 행렬을 자동 생성하는 함수로 추후에도 말뭉치에서 동시발생 행렬을 만들어야 할 때마다 이용할 수 있다.
벡터 간 유사도
동시발생 행렬을 활용해 단어를 벡터로 표현하는 방법을 알아봤으니 이번에는 벡터 사이의 유사도를 측정하는 방법을 알아 보자. 벡터 사이의 유사도를 측정하는 방법은 다양하다. 대표적인 벡터 간 거리 측정법은 유클리드 거리, 맨해튼 거리, 코사인 거리등이 있는데 단어의 벡터 유사도를 나타낼 때는 코사인 유사도를 자주 이용한다. 이때 코사인 유사도는 아래와 같이 계산된다.
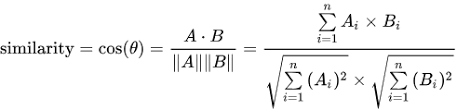
def cos_similarity(x,y):
nx = x/np.sqrt(np.sum(x**2)) #x의 정규화
ny = y/np.sqrt(np.sum(y**2)) #y의 정규화
return np.dot(nx,ny)이때 x나 y에서 인수가 모두 영벡터가 들어오는 경우 divide by zero 문제가 발생하여 eps라는 아주 작은 값을 더해주어 해결한다.
def cos_similarity(x,y,eps=1e-8):
nx = x/np.sqrt(np.sum(x**2) + eps)
ny = y/np.sqrt(np.sum(y**2) + eps)
return np.dot(nx,ny)이번에는 단어 사이의 유사도를 구해보자.
import sys
sys.path.append('..')
from common.util import preprocess, create_co_matrix, cos_similarity
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
C = create_co_matrix(corpus, vocab_size)
c0 = C[word_to_id['you']] # "you"의 단어 벡터
c1 = C[word_to_id['i']] # "i"의 단어 벡터
print(cos_similarity(c0, c1))
# 0.7071067691154799유사 단어 랭킹 표시
어떤 단어가 주어지면 그 단어와 비슷한 단어를 유사도 순으로 출력하는 함수 most_similar()를 구현해보자.
#query: 검색어
#word_to_id: 단어에서 단어 ID로의 딕셔너리
#id_to_word: 단어 ID에서 단어로의 딕셔너리
#word_matrix: 단어 벡터들을 한데 모은 행렬
#top: 상위 몇개까지 출력할지 설정
def most_similar(query, word_to_id, id_to_word, word_matix, top=5):
# 1. 검색어를 꺼낸다.
if query not in word_to_id:
print('%s(을)를 찾을 수 없습니다.' % query)
return
print('\n[query] ' + query)
query_id = word_to_id[query]
query_vec = word_matrix[query_id]
# 2. 코사인 유사도 계산
vocab_size = len(id_to_word)
similarity = np.zeros(vocab_size)
for i in range(vocab_size):
similarity[i] = cos_similarity(word_matrix[i], query_vec)
# 3. 코사인 유사도를 기준으로 내림차순으로 출력
count = 0
for i in (-1 * similarity).argsort():
if id_to_word[i] == query:
continue
print(' %s: %s' % (id_to_word[i], similarity[i]))
count += 1
if count >= top:
return위 코드에서는 검색어의 단어 벡터를 꺼내고 검색어의 단어 벡터와 다른 모든 단어 벡터와의 코사인 유사도를 각각 구한다. 그후 계산한 코사인 유사도 결과를 기준으로 값이 높은 순서대로 출력한다.
이때 argsort() 메서드는 넘파이 배열의 원소를 오름차순으로 정렬한다. (단, 반환값은 배열의 인덱스)
우리는 유사도가 '큰' 순서로 정렬하고 싶으므로 넘파이 배열의 각 원소에 마이너스를 곱한 후 argsort() 메서드를 호출한 것이다.
import sys
sys.path.append('..')
from common.util import preprocess, create_co_matrix, most_similar
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
C = create_co_matrix(corpus, vocab_size)
most_similar('you', word_to_id, id_to_word, C, top=5)
"""
[query] you
goodbye: 0.707167691154799
i: 0.7071067691154799
hello: 0.7071067691154799
say: 0.0
and: 0.0
"""'you'와 가까운 단어를 리스트업하는 코드이다.
'Robotics & AI > DeepLearning' 카테고리의 다른 글
| 딥러닝 직접 구현하기 - (추론 기반 기법) (0) | 2024.02.01 |
|---|---|
| 딥러닝 직접 구현하기 - (통계 기반 기법 개선) (1) | 2024.01.29 |
| Udemy - 딥러닝의 모든 것(AutoEncoder구축하기) (0) | 2024.01.24 |
| 딥러닝 직접 구현하기 - (CNN) (4) | 2024.01.19 |
| 딥러닝 직접 구현하기 - (Training process) (1) | 2024.01.15 |



