Markov Property
마르코프 속성(Markov Property)은 확률론과 통계학, 특히 확률 과정에서 중요한 개념이다. 이는 강화학습의 핵심 문제인 Markov Decision Process를 정의하고 해결하는 것에도 핵심적으로 쓰인다. 이 속성은 미래의 상태가 오직 현재의 상태에만 의존하며 과거의 상태에는 의존하지 않는다는 것을 나타낸다. 해당 특성을 수식화하면 아래와 같이 나타낼 수 있다.

마르코프 속성은 복잡한 확률 과정을 단순화한다. 과거의 모든 정보를 고려할 필요 없이, 현재 상태만을 이용하여 미래를 예측할 수 있다. 또한 마르코프 속성은 계산상의 복잡성을 줄여준다. 과거의 모든 상태를 추적하고 고려하는 대신, 현재 상태만을 고려함으로써 더 효율적인 계산이 가능하다.
마르코프 속성은 모델링을 단순화하지만, 모든 상황에서 현실적이거나 정확하지 않을 수 있다. 예를 들어, 실제 환경에서 미래 상태가 과거의 연속된 상태들에 의존하는 경우가 많다. 이런 경우, 확장된 마르코프 모델이나 비마르코프 과정을 사용할 수 있다.
State transition matrix
상태 전이 행렬(State Transition Matrix)은 마르코프 체인이나 마르코프 결정 과정과 같은 확률 과정에서 상태 간의 전이 확률을 나타내는 행렬이다. 이 행렬은 각 상태에서 다른 상태로의 전이 확률을 체계적으로 표현하는데 사용된다. 이는 아래와 같이 수식으료 표현할 수 있고 이때 P는 행렬로 표현된다.


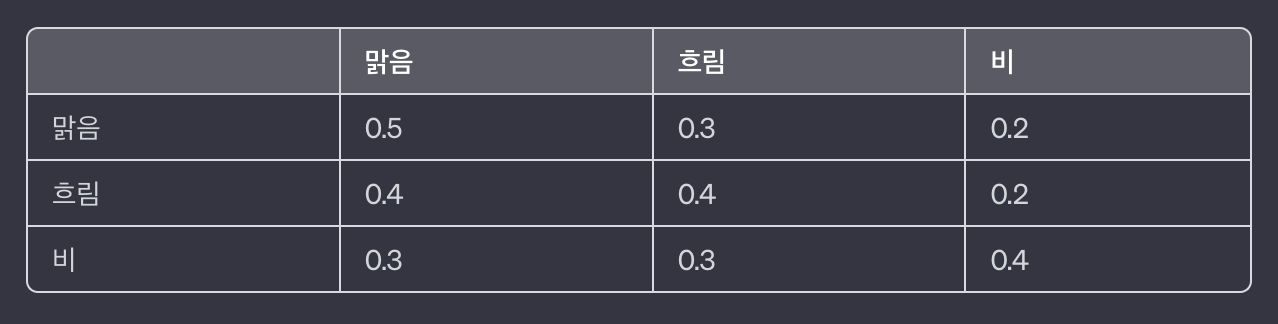
날씨 예측을 예를 들면 아래와 같이 각 상태에 따른 다음 상태의 확률을 지정하여 3X3 행렬을 만들 수 있다.
Markov Process
Markov process는 미래의 상태가 현재의 상태에만 영향을 받는 확률 과정이다. 해당 확률 과정의 기본 구성 요소를 살펴보자. 상태(State)는 마르코프 프로세스에서 시스템이 취할 수 있는 모든 가능한 상태들의 집합이다. 전이 확률(Transition Probability)는 한 상태에서 다른 상태로 이동할 확률을 나타낸다. 이는 보통 전이 확률 행렬로 표현된다. 시작 상태(Initial State)는 프로세스가 시작하는 상태이다. 때때로 시작 상태 분포로도 표현된다. 이때 State의 S와 Transition Probability의 P를 따와서 <S,P>라는 튜플로 표현이 된다.
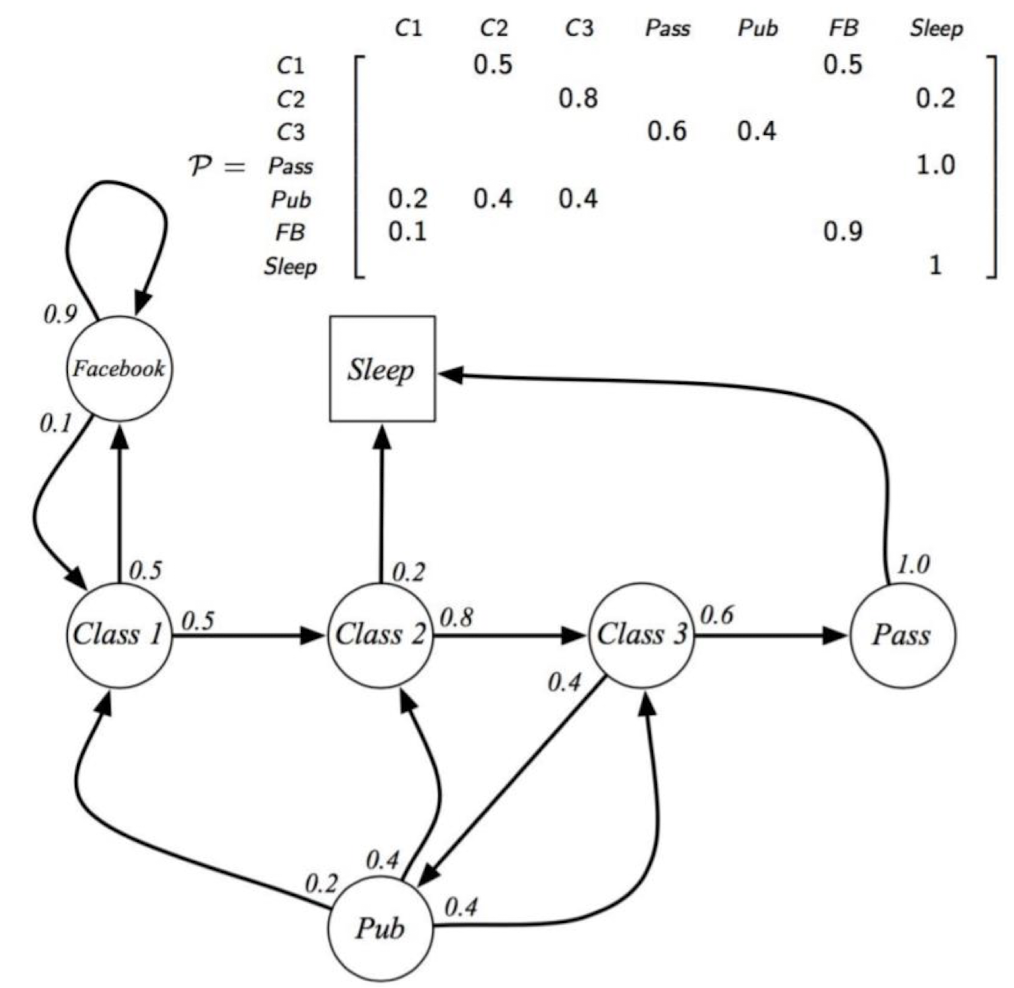
위의 Student Markov Process로 Sleep은 도착하면 더이상 다른 곳으로 가지 않는 시퀀스의 종료를 나타내는 terminal인데 이는 Markov Process에서 반드시 존재하지는 않는다.
Markov Reward Process
마르코프 보상 프로세스(Markov Reward Process, MRP)는 마르코프 프로세스의 확장으로, 각 상태에 특정한 보상이 할당되어 있다. Reward의 개념은 들어가 있지만 action은 아직 포함되지 않은 것을 볼 수 있다. 이제는 튜플에 R과 λ가 추가되어 <S,P,R,γ>로 나타낸다. 각각은 Reward Function과 Discount Factor를 나타낸다. Reward Function은 상태 s에서 상태 s′으로 전이할 때 얻는 보상를 말하고 R로 나타내고 Discount Factor는 미래 보상의 현재 가치를 계산하기 위한 할인 계수로 γ로 나타낸다.
Reward Function 식은 다음과 같고 R_s = E[R_t+1|S_t=s]
γ는 0과 1사이의 숫자이다. γ가 0이라면 즉각적인 보상만 신경쓰겠다는 거고 γ이 1에 가까워질수록 미래의 보상을 더 신경쓰겠다는 것이다.
Return은 아래와 같은 식으로 나타낼 수 있다.
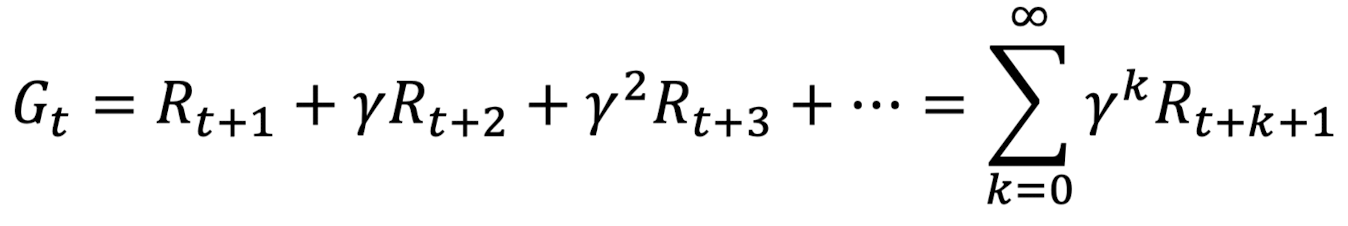
이때 마지막 상태에 도달하고 그 다음번에 다시 처음부터 선택을 시작하는 과정들을 Episode라고 부르는데 T가 마지막 step이라고 할 때 아래와 같이 나타낸다.
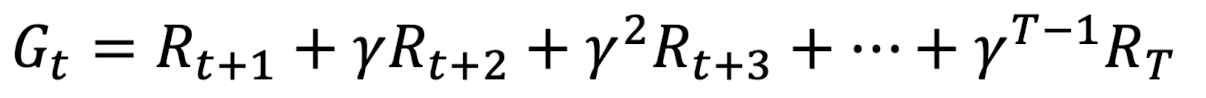
Value function v(s)는 state s에서의 가치를 나타내는 함수로 아래와 같이 식을 쓸 수 있다.
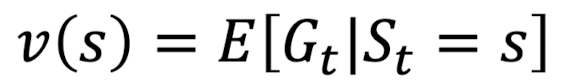

위와 같은 reward값이 부여되었을때 sample return들을 내보자. 시작점은 C1으로 두고 γ=0.5로 두고 실험을 해보면 아래와 같다.

Bellman Equations for MRP
Bellman Equation을 이용하여 위와 같은 수많은 실험을 대신하여 수식적으로 문제를 해결해보려 한다.
Immediate reward를 R_t+1으로 두고 Discounted value of successor state를 γv(S_t+1)이라 할때 아래와 같이 식을 쓸 수 있다.

아래와 같이 당장 받는 보상과 s에서 s'으로 넘어갈때 s'에서의 상태가치들을 더하면 현재 상태인 s의 가치를 알 수 있다는 것이다.

Bellman equation은 v=R+γPv 형태의 matrice form으로 나타낼 수 있다.

Linear equation이니 식 변환을하면 v(s)는 다음과 같이 표현할 수 있다.
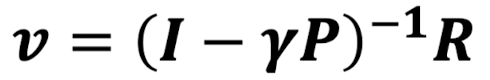
다만 위 식의 computational complexity는 n state에서 O(n^3)로 매우 복잡도가 높다. 따라서 점화식 꼴로 바꿔서 식의 복잡도를 낮춰서 해결하려는 노력이 있다.
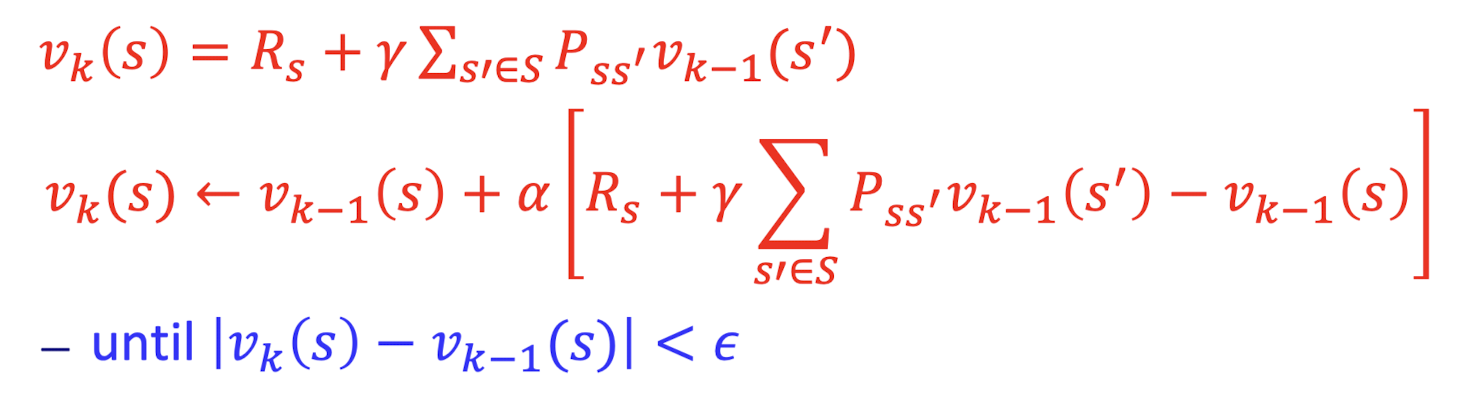
k번째에서는 v_k(s')가 필요한데 위와 같이 iterative 기법을 이용하려면 다음 step의 state value를 알 수 없으니 v_k-1(s')로 대체하여 사용하는 것을 볼 수 있다. 그러나 k번째와 k-1번째 state value의 차이가 매우 줄어들때까지 반복하면 그 결과가 유의미하게 잘 나오기에 이러한 방식으로 대체하여 이용한다.
'Robotics & AI > Reinforcement Learning' 카테고리의 다른 글
| 강화학습 - (BellmanOptEq) (0) | 2024.01.31 |
|---|---|
| 강화학습 - (Markov Decision Process) (0) | 2024.01.25 |
| 강화학습 - (UCB) (1) | 2024.01.13 |
| 강화학습 - (Multi-armed Bandits) (0) | 2024.01.09 |
| 강화학습 - Intro (0) | 2024.01.07 |



