K-armed Bandits
아래의 그림과 같이 여러개의 손으로 Slot machine을 다루는 컨셉에서 시작한 기법이다.

여러개의 Slot machine이 있다는 것은 각기 다른 확률을 갖고 있는 event중 선택을 하여 최선의 결과를 이끌어내야 한다는 것을 의미한다.

위와 같이 5가지 경우가 있다면 D5를 선택하는 것이 좋은 선택이 될 것이다.
이때 좋은 선택을 해내는 가장 간단한 방법은 각각을 몇번씩 선택해보고 그 결과치를 평균을 내어 그 평균값이 최대인 결과를 계속해서 선택하면 될 것이다. 그러나 그런 방법은 안정도는 높은 수 있지만 최선의 방법을 찾기에는 어려움이 있을 수 있다. 따라서 아직 잘 알려지지 않은 팔을 당겨서 더 높은 보상을 주는 팔을 찾는 과정인 exploration과 현재까지 알려진 정보를 바탕으로 가장 높은 보상을 줄 것으로 예상되는 팔을 계속 당기는 exploitation 사이의 균형을 잘 맞춰야한다. 그리고 그 Exploration-Exploitation Tradeoff를 잘 조절하는 것이 K-armed bandit 문제의 핵심이다.

위와 같이 a를 선택하면 a를 선택했을 때의 기대치를 위와 같이 표시한다.
아래는 10개의 action이 있다고 할때 각각의 기대치를 표현해낸 그래프이다.

ε-greedy

위와 같이 기대치가 높은 action을 선택하는 greedy action만을 선택하는 Greedy method도 있으나 이는 초반 몇번의 선택으로 완전히 결정지어버리고 개선의 여지를 두지않기 때문에 최선의 결과를 향해 갈 수 없다.
따라서 Exploration이라는 nongreedy action을 선택하는 과정을 적절히 조합해야하는데 대표적으로 ε-greedy 방법이 있다.
1-ε 확률로 greedy action 즉, Exploitation을 하고 ε의 확률로 random한 action을 하여 Exploration을 진행하는 것이다.


ε이 0.1인 경우, 0.01인경우, 0인 경우를 비교해보니 0.1일때 average reward도 빠르게 상승하고 optimal action을 선택할 확률도 빠르게 상승하는 것을 볼 수 있다.
한 slot machine에서 n번 action이 진행되었을때 그 평균값을 구하는 식에서 NewEstimate을 찾는 식을 구할 수 있다.

위와 같이 점화식을 만들어내어 효율적인 계산을 할 수 있다.

1/n을 이용하여 stepsize를 결정한다면 이는 stationary한 문제에 대해서는 정확히 값을 구해내지만 action의 PDF가 변하는 non-stationary한 문제에 대해서는 정확한 값을 구할 수 없을 것이다. PDF가 변화했는데도 과거의 값과 방금전의 값의 가중치를 갖게 두기 때문이다. non-stationary한 문제에 대해서 유동적으로 대응하기 위해 stepsize를 일정하게 고정하면 아래 식에 따라 최근의 값을 더 잘 반영할 수 있게 된다.

아래는 Convergence condition인데 이는 non-stationary 문제에서는 필요하지만 stationary 문제에서는 그리 매력적인 상태가 아니다.
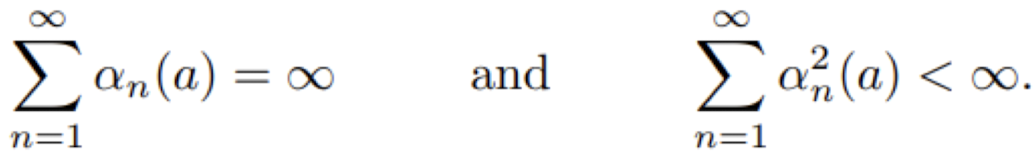
'Robotics & AI > Reinforcement Learning' 카테고리의 다른 글
| 강화학습 - (BellmanOptEq) (0) | 2024.01.31 |
|---|---|
| 강화학습 - (Markov Decision Process) (0) | 2024.01.25 |
| 강화학습 - (Markov Reward Process) (1) | 2024.01.16 |
| 강화학습 - (UCB) (0) | 2024.01.13 |
| 강화학습 - Intro (0) | 2024.01.07 |



