Overfitting
오버피팅은 주로 매개변수가 많아서 표현력이 높은 모델이고 훈련 데이터가 적을 때 발생한다. 데이터에 맞춰서 학습하는 능력이 뛰어난데 맞춰갈 데이터의 수가 적으니 그에 과적합해진다고 생각하면 당연한 조건이다.
이러한 조건에 충족한 상황을 만들어서 오버피팅을 발생시키고 결과를 살펴보자.
60,000개인 MNIST데이터셋중 300개만 사용하고 7층 네트워크를 사용하여 복잡도를 높혀보자. 각 층은 100개의 뉴런, ReLU 활성화 함수를 사용하였다.
from dataset.mnist import load_mnist
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
# 오버피팅을 재현하기 위해 학습 데이터 수를 줄임
x_train = x_train[:300]
t_train = t_train[:300]
import numpy as np
import matplotlib.pyplot as plt
from common.multi_layer_net import MultiLayerNet
#from common.optimizer import SGD
weight_decay_lambda = 0
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
weight_decay_lambda=weight_decay_lambda)
optimizer = SGD(lr=0.01) # 학습률이 0.01인 SGD로 매개변수 갱신
max_epochs = 201
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0
for i in range(1000000000):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
grads = network.gradient(x_batch, t_batch)
optimizer.update(network.params, grads)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("epoch:" + str(epoch_cnt) + ", train acc:" + str(train_acc) + ", test acc:" + str(test_acc))
epoch_cnt += 1
if epoch_cnt >= max_epochs:
break학습과정을 에폭단위로 그래프로 그려서 train, test결과를 비교해보자.
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, train_acc_list, marker='o', label='train', markevery=10)
plt.plot(x, test_acc_list, marker='s', label='test', markevery=10)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
train 데이터에 과적합되어 정확도가 1.0에 수렴하지만 test 데이터에 대한 결과는 개선되지 않는 모습이다.
Weight decay
오버피팅을 억제하기 위해 사용되온 대표적인 기법인 weight decay(가중치 감소)가 있다. 이는 학습 과정에서 가중치가 커질 수록 페널티를 부여하여 오버피팅을 억제하는 것이다. L2 regulation은 가중치의 L2 norm을 손실 함수에 다아여 가중치 증폭을 억제한다. 가중치를 W라 하면 L2 norm에 따른 가중치 감소는 (1/2)*λ*(W^2)이 된다. 이를 손실함수에 더하는 것이다. 여기서 쓰인 λ는 정규화의 세기를 조절하는 하이퍼파라미터이다. λ를 크게 설정할 수록 큰 가중치에 대한 페널티가 커지는 것이다. L2 norm은 각 원소의 제곱들을 더한 방식인데 W = (W1, W2, ..., Wn)이 있다면 아래와 같이된다.

이전에 사용한 코드에서 weight decay lamda를 0.1로 바꾸어 적용해보자.
weight_decay_lambda = 0.1
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
weight_decay_lambda=weight_decay_lambda)
optimizer = SGD(lr=0.01) # 학습률이 0.01인 SGD로 매개변수 갱신
max_epochs = 201
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0
for i in range(1000000000):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
grads = network.gradient(x_batch, t_batch)
optimizer.update(network.params, grads)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("epoch:" + str(epoch_cnt) + ", train acc:" + str(train_acc) + ", test acc:" + str(test_acc))
epoch_cnt += 1
if epoch_cnt >= max_epochs:
break
# 그래프 그리기==========
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, train_acc_list, marker='o', label='train', markevery=10)
plt.plot(x, test_acc_list, marker='s', label='test', markevery=10)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
여전히 test와 train 사이의 차이가 있지만 이전 그래프에 비해서는 현저히 그 차이가 줄었다.
Dropout
Weight decay만으로는 충분히 overfitting을 잡을 수 없어서 드롭아웃이라는 기법을 사용한다.

위와 같이 노드중 일부분을 이용하지 않고 학습하는 것이다.
class Dropout:
def __init__(self, dropout_ratio=0.5):
self.dropout_ratio = dropout_ratio
self.mask = None
def forward(self, x, train_flg=True):
if train_flg:
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
return x * self.mask
else:
return x * (1.0 - self.dropout_ratio)
def backward(self, dout):
return dout * self.mask코드의 핵심은 훈련 시에는 순전파 때마다 self.mask에 삭제할 뉴런을 False로 표시한다는 것이다. self.mask는 x와 형상이 같은 배열을 무작위로 생성하고, 그 값이 dropout_ratio보다 큰 원소만 True로 설정한다. 역전파 때의 동작은 ReLU와 같다. 순전파 때 통과시키지 않은 뉴런은 역전파 때도 신호를 차단한다. Dropout을 적용한 코드를 통해 그래프를 비교해보자.
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net_extend import MultiLayerNetExtend
from common.trainer import Trainer
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
# 오버피팅을 재현하기 위해 학습 데이터 수를 줄임
x_train = x_train[:300]
t_train = t_train[:300]
# 드롭아웃 사용 유무와 비울 설정 ========================
use_dropout = True # 드롭아웃을 쓰지 않을 때는 False
dropout_ratio = 0.2
# ====================================================
network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100],
output_size=10, use_dropout=use_dropout, dropout_ration=dropout_ratio)
trainer = Trainer(network, x_train, t_train, x_test, t_test,
epochs=301, mini_batch_size=100,
optimizer='sgd', optimizer_param={'lr': 0.01}, verbose=False)
trainer.train()
train_acc_list, test_acc_list = trainer.train_acc_list, trainer.test_acc_list
# 그래프 그리기==========
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, marker='o', label='train', markevery=10)
plt.plot(x, test_acc_list, marker='s', label='test', markevery=10)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()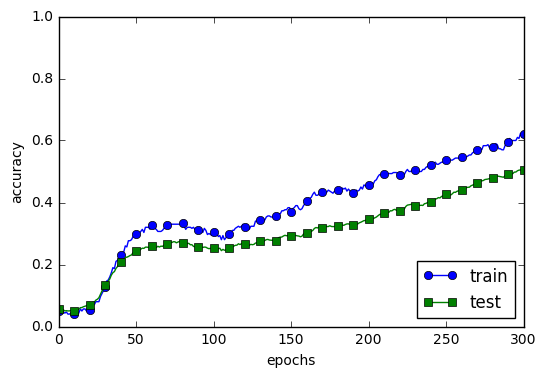
train과 test의 간극이 확실히 줄어든 것을 확인할 수 있다.
하이퍼파라미터
하이퍼파라미터는 각 층의 뉴런수, 배치 크기, 매개변수 갱신 시의 학습률과 가중치 감소와 같은 것들을 이야기한다. 하이퍼파라미터 값을 최대한 효율적으로 탐색하는 방법을 알아보자.
from dataset.mnist import load_mnist
from common.util import shuffle_dataset
(x_train, t_train), (x_test, t_test) = load_mnist()
# 훈련 데이터를 뒤섞는다.
x_train, t_train = shuffle_dataset(x_train, t_train)
# 20%를 검증 데이터로 분할
validation_rate = 0.20
validation_num = int(x_train.shape[0] * validation_rate)
x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]우선 위와 같이 MNIST 데이터셋에서 20%를 미리 분할하여 test 데이터로 나눠둔다. 훈련 데이터를 분리하기 전에 입력 데이터와 정답 레이블을 shuffle_dataset으로 뒤섞어서 데이터 셋 안의 데이터가 치우쳐 있는 상황을 방지한다.
하이퍼파라미터 최적화는 아래의 단계를 거친다.
0단계: 하이퍼파라미터 값의 범위를 설정
1단계: 설정된 범위에서 하이퍼파라미터의 값을 무작위로 추출
2단계: 1단계에서 샘플링한 하이퍼파라미터 값을 사용하여 학습하고, 정확도를 평가. (에폭은 작게 설정)
3단계: 1단계와 2단계를 특정 횟수(100회 등) 반복하며, 그 정확도의 결과를 보고 하이퍼파라미터의 범위를 좁힌다.
# 하이퍼파라미터 무작위 추출코드
weight_decay = 10**np.random.uniform(-8,-4)
lr = 10**np.random.uniform(-6,-2)import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net import MultiLayerNet
from common.util import shuffle_dataset
from common.trainer import Trainer
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
# 결과를 빠르게 얻기 위해 훈련 데이터를 줄임
x_train = x_train[:500]
t_train = t_train[:500]
# 20%를 검증 데이터로 분할
validation_rate = 0.20
validation_num = x_train.shape[0] * validation_rate
x_train, t_train = shuffle_dataset(x_train, t_train)
x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]
def __train(lr, weight_decay, epocs=50):
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100],
output_size=10, weight_decay_lambda=weight_decay)
trainer = Trainer(network, x_train, t_train, x_val, t_val,
epochs=epocs, mini_batch_size=100,
optimizer='sgd', optimizer_param={'lr': lr}, verbose=False)
trainer.train()
return trainer.test_acc_list, trainer.train_acc_list
# 하이퍼파라미터 무작위 탐색======================================
optimization_trial = 100
results_val = {}
results_train = {}
for _ in range(optimization_trial):
# 탐색한 하이퍼파라미터의 범위 지정===============
weight_decay = 10 ** np.random.uniform(-8, -4)
lr = 10 ** np.random.uniform(-6, -2)
# ================================================
val_acc_list, train_acc_list = __train(lr, weight_decay)
print("val acc:" + str(val_acc_list[-1]) + " | lr:" + str(lr) + ", weight decay:" + str(weight_decay))
key = "lr:" + str(lr) + ", weight decay:" + str(weight_decay)
results_val[key] = val_acc_list
results_train[key] = train_acc_list
# 그래프 그리기========================================================
print("=========== Hyper-Parameter Optimization Result ===========")
graph_draw_num = 20
col_num = 5
row_num = int(np.ceil(graph_draw_num / col_num))
i = 0
for key, val_acc_list in sorted(results_val.items(), key=lambda x:x[1][-1], reverse=True):
print("Best-" + str(i+1) + "(val acc:" + str(val_acc_list[-1]) + ") | " + key)
plt.subplot(row_num, col_num, i+1)
plt.title("Best-" + str(i+1))
plt.ylim(0.0, 1.0)
if i % 5: plt.yticks([])
plt.xticks([])
x = np.arange(len(val_acc_list))
plt.plot(x, val_acc_list)
plt.plot(x, results_train[key], "--")
i += 1
if i >= graph_draw_num:
break
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net import MultiLayerNet
from common.util import shuffle_dataset
from common.trainer import Trainer
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
# 결과를 빠르게 얻기 위해 훈련 데이터를 줄임
x_train = x_train[:500]
t_train = t_train[:500]
# 20%를 검증 데이터로 분할
validation_rate = 0.20
validation_num = x_train.shape[0] * validation_rate
x_train, t_train = shuffle_dataset(x_train, t_train)
x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]
def __train(lr, weight_decay, epocs=50):
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100],
output_size=10, weight_decay_lambda=weight_decay)
trainer = Trainer(network, x_train, t_train, x_val, t_val,
epochs=epocs, mini_batch_size=100,
optimizer='sgd', optimizer_param={'lr': lr}, verbose=False)
trainer.train()
return trainer.test_acc_list, trainer.train_acc_list
# 하이퍼파라미터 무작위 탐색======================================
optimization_trial = 100
results_val = {}
results_train = {}
for _ in range(optimization_trial):
# 탐색한 하이퍼파라미터의 범위 지정===============
weight_decay = 10 ** np.random.uniform(-8, -4)
lr = 10 ** np.random.uniform(-6, -2)
# ================================================
val_acc_list, train_acc_list = __train(lr, weight_decay)
print("val acc:" + str(val_acc_list[-1]) + " | lr:" + str(lr) + ", weight decay:" + str(weight_decay))
key = "lr:" + str(lr) + ", weight decay:" + str(weight_decay)
results_val[key] = val_acc_list
results_train[key] = train_acc_list
# 그래프 그리기========================================================
print("=========== Hyper-Parameter Optimization Result ===========")
graph_draw_num = 20
col_num = 5
row_num = int(np.ceil(graph_draw_num / col_num))
i = 0
for key, val_acc_list in sorted(results_val.items(), key=lambda x:x[1][-1], reverse=True):
print("Best-" + str(i+1) + "(val acc:" + str(val_acc_list[-1]) + ") | " + key)
plt.subplot(row_num, col_num, i+1)
plt.title("Best-" + str(i+1))
plt.ylim(0.0, 1.0)
if i % 5: plt.yticks([])
plt.xticks([])
x = np.arange(len(val_acc_list))
plt.plot(x, val_acc_list)
plt.plot(x, results_train[key], "--")
i += 1
if i >= graph_draw_num:
break
plt.show()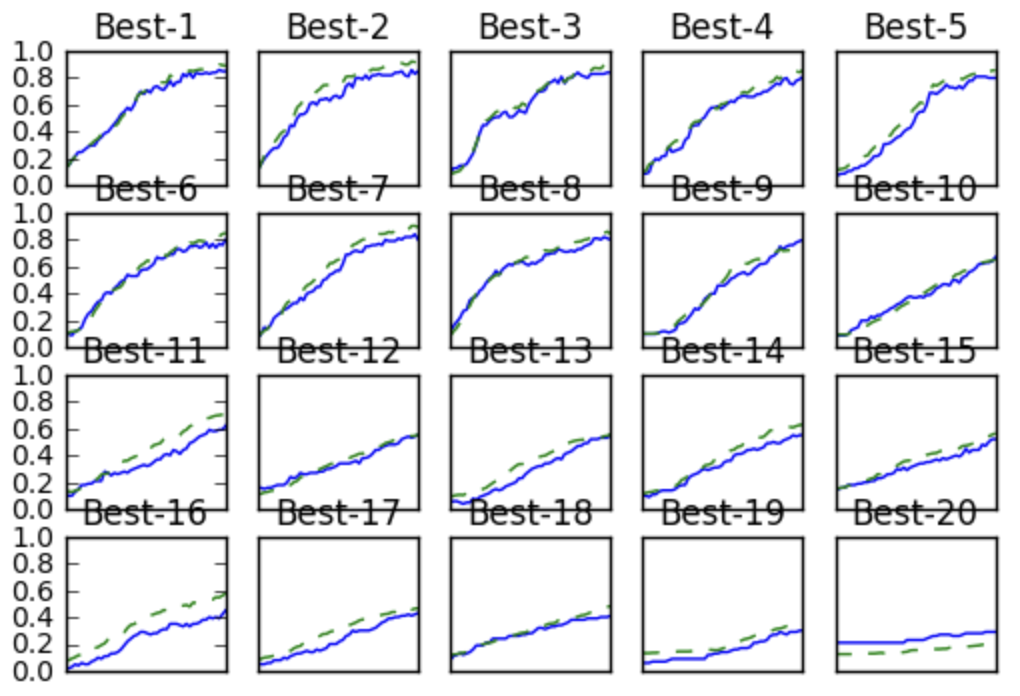
Best-5 정도까지 학습이 순조롭게 진행된다. 결과로 볼 때 학습률은 0.001 ~ 0.01, 가중치 감소 계수는 10-8 ~ 10-6 정도임을 알 수 있다. 다음은 축소된 범위로 똑같은 작업을 반복한다. 범위를 좁혀가다가 특정 단계에서 최종 하이퍼파라미터 값을 하나 선택한다.
'Robotics & AI > DeepLearning' 카테고리의 다른 글
| Udemy - 딥러닝의 모든 것(AutoEncoder구축하기) (0) | 2024.01.24 |
|---|---|
| 딥러닝 직접 구현하기 - (CNN) (4) | 2024.01.19 |
| Udemy - 딥러닝의 모든 것(AutoEncoders) - (2) (1) | 2024.01.11 |
| 딥러닝 직접 구현하기 - (배치 정규화) (1) | 2024.01.11 |
| Udemy - 딥러닝의 모든 것(AutoEncoders) - (1) (1) | 2024.01.10 |



