NLP를 위한 합성곱 신경망
CNN은 주로 vision 분야에서 사용되는 알고리즘이지만 이를 응용해서 자연어 처리에 사용하기 위한 방법들이 연구되고 있다. 합성곱 신경망이 어떤식으로 텍스트 처리에서 쓰일 수 있는지 알아보자. 우선 합성곱 신경망에 대해서 알아보자.

위는 합성곱 신경망의 기본적인 구조이다. CONV는 합성곱 연산이고 그 결과가 활성화 함수 ReLU를 통과한다. 이때 CONV와 ReLU를 합쳐서 합성곱층이라고 한다. 다음으로 POOL은 풀링 연산을 하는 부분이고 풀링층이라고 한다.
합성곱 신경망이 조명받은 이유는 아래에서 볼 수 있다.
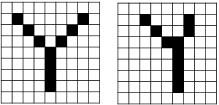
위와 같이 정자로 쓴 Y가 있고 조금 흘려쓴 Y가 있을때 이를 1차원 텐서로 변환하여 일반적으로 분석하려하면 문제가 발생한다.

위 그림을 보면 느낌이 오겠지만 형태에 대한 정보가 잘 반영되지 않는다. 이 값을 Y라고 판단하기엔 어려움이 있을것이다.
따라서 Convolution을 이용하여 입력값의 특을 담은 축소된 텐서를 만들어서 학습에 이용한다. 그 과정을 보면 아래와 같다.
첫번째 스텝

두번째 스텝
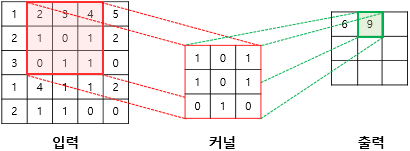
세번째 스텝

.
.
.
위와 같이 입력으로부터 커널을 사용하여 합성곱 연산을 통해 나온 결과를 특성 맵(feature map)이라고 한다.
위의 예제에서는 커널의 크기가 3 × 3이었지만, 커널의 크기는 사용자가 정할 수 있다. 또한 커널의 이동 범위가 위의 예제에서는 한 칸이었지만, 이 또한 사용자가 정할 수 있다. 이러한 이동 범위를 스트라이드(stride)라고 한다.
아래의 예제는 스트라이드가 2일 경우에 5 × 5 이미지에 합성곱 연산을 수행하는 3 × 3 커널의 움직임을 보인다. 최종적으로 2 × 2의 크기의 특성 맵을 얻을 수 있다.

더 자세한건 CNN 설명글에서 더 다뤄보도록하자.
자연어 처리를 위한 1D CNN
1D 합성곱 연산에서도 입력이 되는 것은 각 단어가 벡터로 변환된 문장 행렬로 LSTM과 입력을 받는 형태는 동일하다.
'wait for the video and don't rent it'이라는 문장이 있을 때, 이 문장이 토큰화, 패딩, 임베딩 층(Embedding layer)을 거친다면 다음과 같은 문장 형태의 행렬로 변환다. 아래 그림에서 n은 문장의 길이, k는 임베딩 벡터의 차원다.

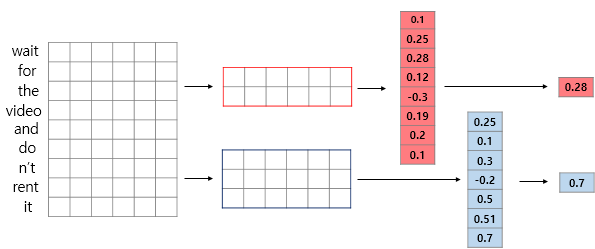
1D 합성곱 연산에서 커널의 너비는 문장 행렬에서의 임베딩 벡터의 차원과 동일하게 설정된다. 그렇기 때문에 1D 합성곱 연산에서는 커널의 높이만으로 해당 커널의 크기라고 간주한다. 가령, 커널의 크기가 2인 경우에는 아래의 그림과 같이 높이가 2, 너비가 임베딩 벡터의 차원인 커널이 사용된다. 그러한 연산을 지속적으로 진행하는 것이다.

이미지 처리에서의 CNN에서 그랬듯이, 일반적으로 1D 합성곱 연산을 사용하는 1D CNN에서도 합성곱 층(합성곱 연산 + 활성화 함수) 다음에는 풀링 층을 추가하게된다. 그 중 대표적으로 사용되는 것이 맥스 풀링(Max-pooling)이다. 맥스 풀링은 각 합성곱 연산으로부터 얻은 결과 벡터에서 가장 큰 값을 가진 스칼라 값을 빼내는 연산이다.
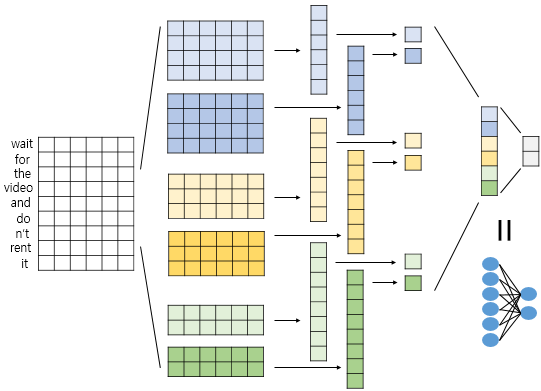
위의 개념들을 이용하여 신경망을 설계해보자. 이진 분류를 위한 신경망을 설계했기 때문에 출력층에서 뉴런의 개수가 2이고 softmax함수를 이용한다. 커널은 크기가 4인 커널 2개, 3인 커널 2개, 2인 커널 2개를 사용한다. 문장의 길이가 9인 경우, 합성곱 연산을 한 후에는 각각 6차원 벡터 2개, 7차원 벡터 2개, 8차원 벡터 2개를 얻는다. 벡터가 6개므로 맥스 풀링을 한 후에는 6개의 스칼라 값을 얻는데, 일반적으로 이렇게 얻은 스칼라값들은 전부 연결(concatenate)하여 하나의 벡터로 만들어준다. 이렇게 얻은 벡터는 1D CNN을 통해서 문장으로부터 얻은 벡터이다. 이를 뉴런이 2개인 출력층에 완전 연결시키므로서(Dense layer를 사용) 텍스트 분류를 수행한다.
'Robotics & AI > DeepLearning' 카테고리의 다른 글
| Udemy - 딥러닝의 모든 것(CNN 구축하기) (0) | 2023.09.05 |
|---|---|
| GAN (0) | 2023.07.26 |
| 딥러닝 직접 구현하기 - (신경망 학습) (0) | 2023.07.06 |
| 딥러닝 직접 구현하기 - (신경망) (0) | 2023.07.01 |
| 딥러닝 직접 구현하기 - (퍼셉트론) (0) | 2023.06.21 |



