Quick sort algorithm
퀵정렬은 pivot을 설정하고 설정한 pivot을 기준으로 작은 요소들은 모두 pivot의 왼쪽으로 옮겨지고 pivot보다 큰 요소들은 모두 pivot의 오른쪽으로 옮긴다. pivot을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬하고 분할된 부분 리스트에 대하여 recursion을 이용하여 정렬을 반복한다. 이때 quick sort는 unstable sorting process이다.
나누어진 리스트에서도 다시 pivot을 정하고 pivot을 기준으로 2개의 부분 리스트로 나누는 과정을 반복한다.
이때도 merge sort와 같이 divide and conquer 과정을 통해 진행이 됨을 알 수 있다.
추가적으로 pivot을 설정하는 다양한 방법이 있는데 pivot을 설정하는 방식이 quick sort algorithm의 성능을 결정하는 중요한 요소이기 때문에 pivot을 결정하는 과정이 중요하다. pivot은 중간값에 가까울 수록 좋은 pivot이라고 할 수 있다.

Source code
ArrayVector header file과 cpp file은 이전의 merge sort algorithm에서 참고하자
quicksort.cpp
#include "ArrayVector.h"
#include <tuple>
#include <string>
#include <iostream>
#include <random> //난수생성을 위한 library
#include <sstream> //string으로 형변환을 위한 library
#include <chrono> //실행시간 측정을 위한 library
using namespace std;
void QuickSort(ArrayVector& vec, int L, int H)
{
int l, r, M;
if (H - L > 1) {
//pivot 설정하기
M = (L + H) / 2; //M은 L,H의 중간값
//L,M,H에 해당하는 data중 중간값을 찾아서 pivot으로 설정
if (get<1>(vec[L]) > get<1>(vec[M]))
swap(vec[L], vec[M]);
if (get<1>(vec[L]) > get<1>(vec[H]))
swap(vec[L], vec[H]);
if (get<1>(vec[M]) > get<1>(vec[H]))
swap(vec[M], vec[H]);
swap(vec[M], vec[H - 1]);
//찾은 중간값을 pivot으로 설정
tuple<string, int>& pivot = vec[H - 1];
//L을 l에 담고 H-1을 담고 r에 담음
l = L;
r = H - 1;
while (true) {
while (get<1>(vec[++l]) < get<1>(pivot)); // l+1의 data가 pivot의 data보다 작고
while (get<1>(vec[--r]) > get<1>(pivot)); // r-1의 data가 pivot의 data보다 크면 진행
if (l >= r) break; //l이 r보다 크거나 같아지면 반복문 정지
swap(vec[l], vec[r]); //반복문이 정지되지 않으면 vec[l]과 vec[r]을 swap
}
swap(vec[l], vec[H - 1]); //반복문이 종료되면 vec[l]과 vec[H-1]을 swap
//두개로 나누어 recursion진행
QuickSort(vec, L, l - 1);
QuickSort(vec, l + 1, H);
}
//vec[L]의 data가 vec[H]의 data보다 크면
else if (get<1>(vec[L]) > get<1>(vec[H]))
swap(vec[L], vec[H]); //vec[L]과 vec[H] swap
}
int main() {
//실행 시간 측정을 위해 main문 시작지점 시간 측정
auto start = std::chrono::system_clock::now();
ArrayVector vec;
string key;
uniform_int_distribution<int> dis(0, 30000); // 0~1000사이 균등분포 선언
//난수를 생성하기위한 메르텐 트위스트 함수 이용
random_device rd;
mt19937_64 gen(rd());
for (int j = 0; j < 30000; j++)
{
int data = dis(gen);
std::stringstream s;
s << j; //int값인 j를 string으로 변환가능 상태인 s로 변환
key = "key" + s.str(); // key(숫자) 모양으로 key값 생성
vec.insert(j, { key , data }); //값 insert
}
//before sorting
cout << "before sorting" << endl;
for (int i = 0; i < vec.size(); i++) {
cout << "<" << get<0>(vec[i]) << ", " << get<1>(vec[i]) << ">" << endl;
}
//InsertionSort 진행
QuickSort(vec, 0, vec.size() - 1);
//after sorting
cout << endl << "after sorting" << endl;
for (int i = 0; i < vec.size(); i++) {
cout << "<" << get<0>(vec[i]) << ", " << get<1>(vec[i]) << ">" << endl;
}
//실행 시간 측정을 위해 main문 종료직전 시간 측정
auto end = std::chrono::system_clock::now();
//시작시간과 종료시간의 차를 구해서 그 시간을 출력
std::chrono::duration<double> elapsed_seconds = end - start;
std::cout << "실행시간: " << elapsed_seconds.count() << " sec" << std::endl;
return 0;
}성능 분석
시간복잡도를 분석해보면 다음과 같이 계산됨을 알 수 있다.
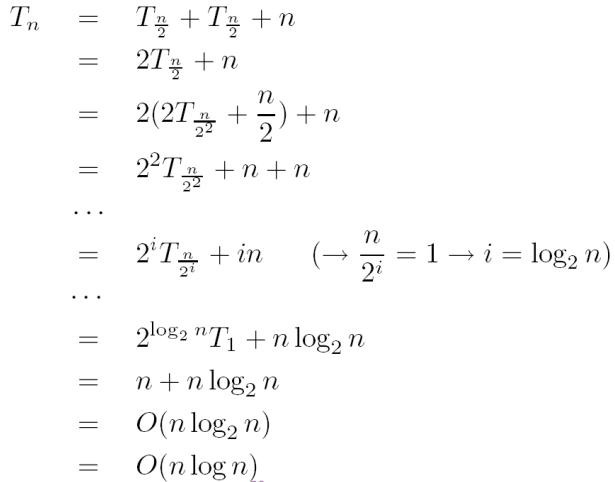
시간복잡도는 n+nlog2n, 즉 O(nlogn)이고 이는 앞에서 다룬 다섯가지의 sorting algorithm중 가장 빠른 정렬 방법이다.
마지막으로 다룬 sorting algorithm인 만큼 앞서 다룬 다섯가지 sorting algorithm들의 stable 여부와 시간복잡도를 다시 복습하자.

'Programming Language Training > C & C++' 카테고리의 다른 글
| Merge sort (0) | 2022.12.22 |
|---|---|
| C++ 난수 생성 (0) | 2022.11.17 |
| Bubble sort, Insertion sort, Selection sort (0) | 2022.11.08 |

