Analysis of Algorithms
이전에 간단하게 복잡도 분석에 대해서 배웠으나 이제 본격적으로 알고리즘들을 분석하는 방법을 공부하였다.

대표적인 복잡도 분석 방법중 하나인 Big-O notation에 대한 개괄적인 설명이다.
Big-O notation은 worst-case를 고려한 복잡도 분석법으로 복잡도 증가율의 상한(upper bound)를 나타낸다.
Calculation
어떤 알고리즘을 7가지로 분류하기 위해 연산을 진행할 때는 기본적으로 Tight upper bound를 찾고자 진행한다.
예시를 통해 기본적인 연산 과정을 학습하였다.
Ex1
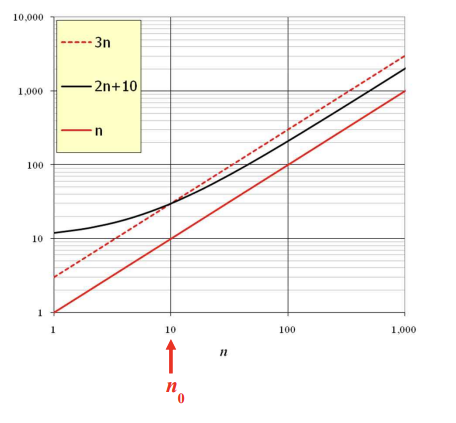
Example: 2n + 10 is O(n)
2n+10 <= cn
(c-2)n >= 10
n >= 10/(c-2)
Pick c=3 and n0 = 10
Ex2
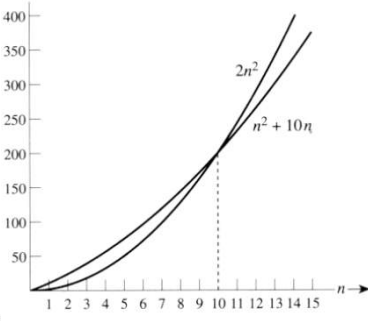
Example: n^2 + 10n is O(n^2)
n^2 + 10n <= cn^2
Pick c=2 and n0=10
이렇게 열심히 알고리즘을 분류하고 복잡도를 조사하는 이유는 아래의 표를 보면 알 수 있다. 같은 기능을 하는 프로그램이 복잡도 level에 따라 얼마나 시간차이가 많이나는지 볼 수 있는 표이다.

알고리즘 효율
int fibo(int n)
{
if(n<=1)
return n;
else
return fibo(n-1) + fibo(n-2);
}재귀적 방법
T(n) = 2^(n/2)
int fibo2(int n){
int i,f[MAX_SIZE];
f[0] = 0;
if(n>0){
f[1] = 1;
for(i=2;i<=n;i++)
f[i] = f[i-1] + f[i-2];
}
return f[n];
}반복적 방법
T(n) = n+1
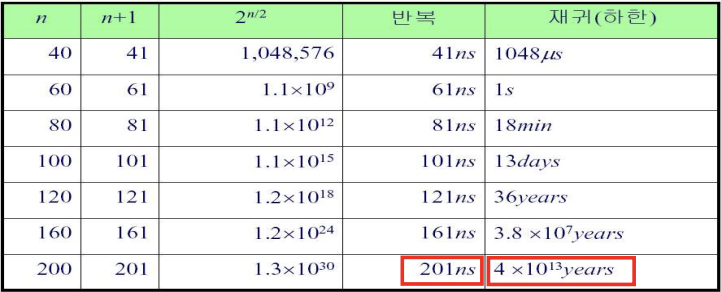
피보나치 수열 구현을 통해 알고리즘 효율성을 비교해보았다. 함수 재귀 호출을 처음 배웠을 때는 피보나치 수열을 굉장히 간단하게 해결한 것 같아서 멋있는 것 같았지만 이렇게 보니 굉장히 바보같은 코드이고 단순히 재귀 호출을 배우기에 적절한 예시일뿐이었다는 것을 알게 되었다.
Linear Recursion
재귀 호출이 단 한번있는 경우로 주어진 문제의 첫번째 또는 마지막 원소와 나머지로 구분하는 경우에 유용하다.
계산방법: 1) n에 대하여 재귀성질을 파악
2) i로 일반화
3) i를 구하고 대입
power 계산 알고리즘
<pseudo code>
Algorithm power(x,n)
Input:A number x and an integer n>=0
Output:The value x^n
if n=0 then
return 1.0
else
return power(x,n-1)*nTn = 1 + Tn-1
= 1 + 1 + Tn-2
= 1 + 1 + 1 + Tn-3
..........
= n-1 + T1
=> O(n)
<pseudo code>
Algorithm power(x,n)
Input:A number x and an integer n>=0
Output:The value x^n
if n=0 then
return 1.0
if n is odd then
y <- power(x,(n-1)/2)
return x*y*y
else
y <- power(x, n/2)
return y*yTn = 1 + Tn/2
= 1 + 1 +Tn/4
= 1 + 1 + 1 + Tn/8
............
= i +Tn/2^i
............
=log2(n) + T1
=log2(n) + 1
=>O(logn)
효율적인 코딩으로 O(n)에서 O(logn)까지 복잡도를 낮출 수 있었다. 그러나 현실에서는 쉽지 않은 과정일 것 같았다.
Higher-Order Recursion
재귀 알고리즘내에서 하나 이상의 재귀호출이 있는 경우
binary recursion(가장 일반적인 형태의 재귀)
<psuedo code>
Algorithm BinarySum(A,i,n)
Input: An integer array A and integers i and n
Output: The reversal of the n integers in A starting at index i
if n=1 then
return A[i]
return BinarySum(A,i,[n/2])+BinarySum(A,i+[n/2],[n/2])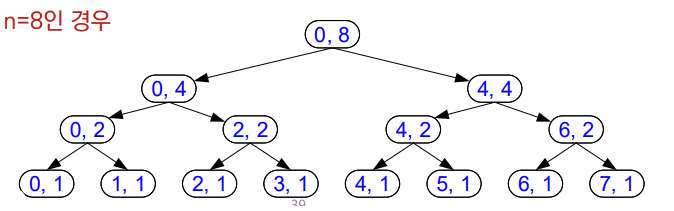

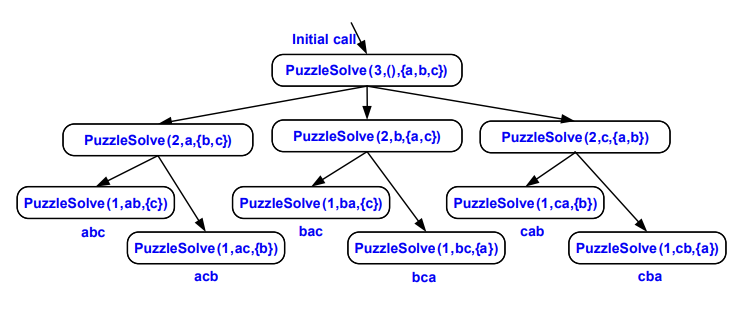
Multiple recursion
재귀호출을 3번 이상 실시하는 경우
'Univ. Study > Data structure' 카테고리의 다른 글
| ArrayStack(2) (0) | 2022.11.19 |
|---|---|
| ArrayStack(1) (0) | 2022.11.18 |
| 자료구조론(4) (1) | 2022.10.03 |
| 자료구조론(3) (0) | 2022.09.26 |
| 자료구조론(2) (0) | 2022.09.12 |

