Graph
Graph는 현상이나 사물을 정점(vertex)과 간선(edge)으로 표현한 것이다. Graph G = (V, E)으로 표현이 되고 이때 V는 정점 집합 E는 간선 집합이다. 두 정점이 간선으로 연결되어 있으면 인접하다고 한다. 인접은 adjacent라고 하고 간선은 두 정점의 관계를 나타낸다. 간단한 예시를 통해 다양한 그래프를 살펴보자.

인간관계를 그래프로 표현한 그래프다.

간선에 weight가 생겨 관계의 깊이를 표현한 그래프다.

방향을 고려한 유향 그래프이다.

두 요소가 결합된 가중치를 가진 유향 그래프이다.
이러한 그래프 구조를 traversal하는 대표적인 두가지 기법 BFS, DFS를 살펴보자.
BFS

BFS는 너비 우선 탐색(breadth first search)의 준말이다. 말그대로 한 정점을 기준으로 주변 정점을 모두 조사하고 넘어가는 것이다. 수행 과정을 간단하게 살펴보자.
(1) 정점 i를 방문한다.
(2) 정점 i에 인접한 정점 중에서 아직 방문하지 않은 정점이 있으면, 이 정점들을 모두 큐에 저장한다.
(3) 큐에서 정점을 삭제하여 새로운 i를 설정하고, 단계 (1)을 수행한다.
(4) 큐가 공백이 되면 연산을 종료한다.
정점 방문 여부를 표시하기 위해 배열 visited[n]을 이용하여 표현한다.
visited[i] = true이면 방문하였다고 판단하고 visited[i] = false이면 방문하지 않았다고 판단한다.

간단한 예시를 통해 BFS가 어떻게 작동하는지 살펴보자.

DFS
DFS는 깊이 우선 탐색(depth first search)의 준말이다. 깊이 파고들며 끝까지 탐색하는 알고리즘이다. 수행과정을 간단히 살펴보자.
(1) 정점 i를 방문한다.
(2) 정점 i에 인접한 정점 중에서 아직 방문하지 않은 정점이 있으면, 이 정점들을 모두 스택에 저장한다.
(3) 스택에서 정점을 삭제하여 새로운 i를 설정하고, 단계 (1)을 수행한다.
(4) 스택이 공백이 되면 연산을 종료한다.
정점 방문 여부는 BFS와 똑같이 표시한다.
visited[i] = true이면 방문하였다고 판단하고 visited[i] = false이면 방문하지 않았다고 판단한다.

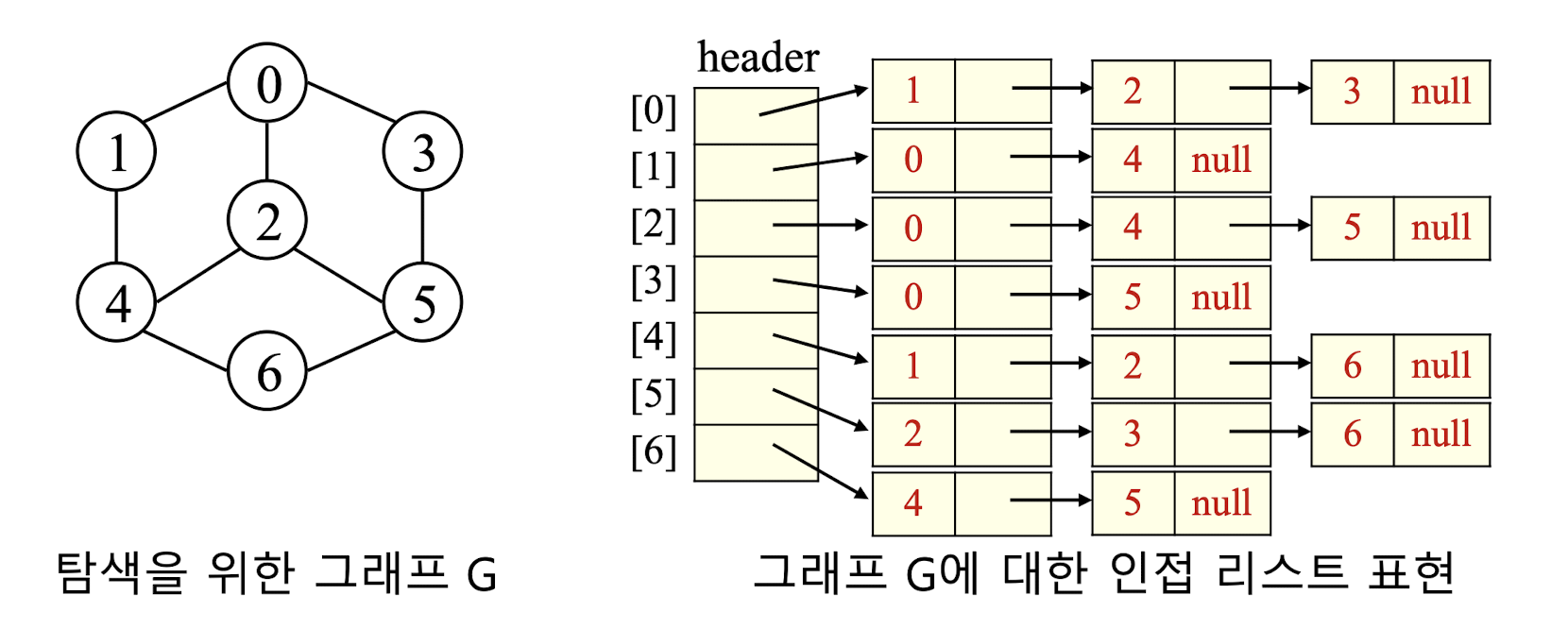
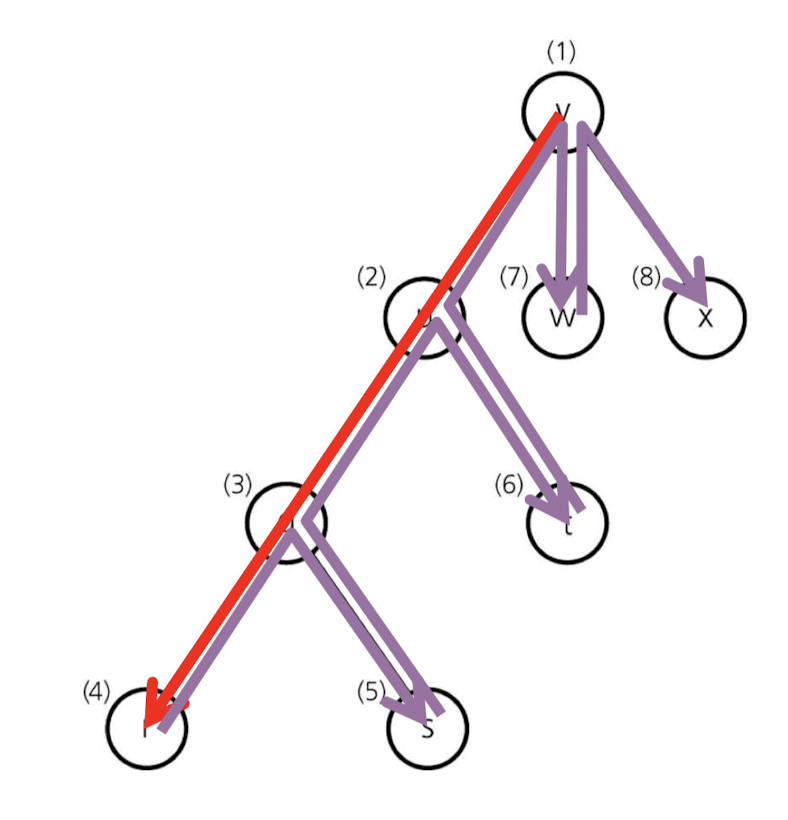
위의 예시를 통해 Stack에 데이터가 어떻게 push, pop되는지 살펴보자.
우선 0으로 시작하기때문에 stack에 1,2,3이 순서대로 push되고 바로 맨위의 3이 pop되고 3에 의해 0과 5가 push되어야 하는데 0은 처음에 pop된거랑 마찬가지 이므로 이미 방문했다고 표시되어 5만 push가 된다. 바로 5가 pop이되고 5의 인접 노드인 2,3,6이 push되는데 2,3은 이미 push되었던 방문 노드이므로 6만 push가 된다. 이와 같은 과정이 반복적으로 진행되며 아래와 같이 탐색이 종료된다.

위 방식은 Stack을 활용한 recursive 방법이다. 다음으로 iterative 기법을 살펴보자.

위 방법은 stack을 사용하지 않고 인접노드를 전부 끝까지 조사하는 방법이다. 재귀 기법을 사용하기 때문에 preorder traversal과 약간은 유사한 느낌을 받을 수 있다.


'Univ. Study > Algorithm Design' 카테고리의 다른 글
| Algorithm design - 최단경로 (0) | 2024.05.30 |
|---|---|
| Algorithm design - MST (0) | 2024.05.28 |
| 알고리즘 설계 실습 - 최적 경로 찾기 (0) | 2024.05.23 |
| Algorithm design - TSP(Traveling Salesperson Problem) (0) | 2024.05.21 |
| 알고리즘 설계 실습 - 연쇄 행렬 곱셈 (0) | 2024.05.16 |


