문제
▪ 9x9 Gaussian filter를 구현하고 결과를 확인할 것
▪ 9x9 Gaussian filter를 적용했을 때 히스토그램이 어떻게 변하는지 확인할 것
▪ 영상에 Salt and pepper noise를 주고, 구현한 9x9 Gaussian filter를 적용해볼 것
▪ 45도와 135도의 대각 에지를 검출하는 Sobel filter를 구현하고 결과를 확인할 것
▪ 컬러영상에 대한 Gaussian pyramid를 구축하고 결과를 확인할 것
▪ 컬러영상에 대한 Laplacian pyramid를 구축하고 복원을 수행한 결과를 확인할 것
#include <opencv2/opencv.hpp>
#include <cmath>
#include <vector>
using namespace cv;
using namespace std;
//3X3 커널 구현
int myKernelConv3x3(const Mat& src, int kernel[][3], int x, int y, int channel, int width, int height) {
int sum = 0;
int sumKernel = 0;
const uchar* srcData = src.ptr<uchar>();
for (int j = -1; j <= 1; j++) {
for (int i = -1; i <= 1; i++) {
int newY = y + j;
int newX = x + i;
if (newY >= 0 && newY < height && newX >= 0 && newX < width) {
sum += srcData[(newY * width + newX) * 3 + channel] * kernel[j + 1][i + 1];
sumKernel += kernel[j + 1][i + 1];
}
}
}
return sumKernel != 0 ? sum / sumKernel : sum;
}
// 9X9 커널 구현
int myKernelConv9x9(const Mat& src, int kernel[][9], int x, int y, int channel, int width, int height) {
int sum = 0;
int sumKernel = 0;
const uchar* srcData = src.ptr<uchar>();
for (int j = -4; j <= 4; j++) {
for (int i = -4; i <= 4; i++) {
int newY = y + j;
int newX = x + i;
if (newY >= 0 && newY < height && newX >= 0 && newX < width) {
sum += srcData[(newY * width + newX) * 3 + channel] * kernel[j + 4][i + 4];
sumKernel += kernel[j + 4][i + 4];
}
}
}
return sumKernel != 0 ? sum / sumKernel : sum;
}
// 3x3 가우시안 필터
Mat myGaussianFilter3x3(Mat srcImg) {
int width = srcImg.cols;
int height = srcImg.rows;
Mat dstImg = srcImg.clone();
int kernel[3][3] = { 1, 2, 1,
2, 4, 2,
1, 2, 1 };
for (int y = 0; y < srcImg.rows; y++) {
for (int x = 0; x < srcImg.cols; x++) {
for (int c = 0; c < 3; c++) { // RGB 채널 각각에 대해 필터 적용
dstImg.at<Vec3b>(y, x)[c] = myKernelConv3x3(srcImg, kernel, x, y, c, srcImg.cols, srcImg.rows);
}
}
}
return dstImg;
}
// 9x9 가우시안 필터
Mat myGaussianFilter9x9(const Mat& srcImg) {
int width = srcImg.cols;
int height = srcImg.rows;
Mat dstImg = srcImg.clone();
int kernel[9][9] = { 1, 3, 5, 7, 8, 7, 5, 3, 1,
3, 6, 11, 16, 18, 16, 11, 6 , 3,
5 ,11, 21, 30, 34, 30, 21, 11, 5,
7, 16, 30, 43, 49, 43, 30, 16, 7,
8 ,18, 34, 49 ,55, 49, 34, 18, 8,
7, 16, 30, 43 ,49, 43, 30, 16, 7,
5 ,11, 21, 30, 34, 30, 21, 11, 5,
3 ,6 ,11, 16, 18 ,16 ,11, 6 ,3,
1 ,3, 5, 7, 8, 7 ,5 ,3, 1 };
for (int y = 0; y < srcImg.rows; y++) {
for (int x = 0; x < srcImg.cols; x++) {
for (int c = 0; c < 3; c++) { // RGB 채널 각각에 대해 필터 적용
dstImg.at<Vec3b>(y, x)[c] = myKernelConv9x9(srcImg, kernel, x, y, c, srcImg.cols, srcImg.rows);
}
}
}
return dstImg;
}
// salt&pepper 노이즈 추가함수
Mat addSaltPepperNoise(const Mat& src, int num) {
Mat img = src.clone(); // 이미지의 복사본을 생성
srand(time(0)); // 난수 생성기 초기화
for (int i = 0; i < num; i++) {
int x = rand() % img.cols;
int y = rand() % img.rows;
bool salt = rand() % 2 == 0;
if (img.channels() == 1) {
img.at<uchar>(y, x) = salt ? 255 : 0; // 흑백 이미지의 경우
}
else {
Vec3b color = salt ? Vec3b(255, 255, 255) : Vec3b(0, 0, 0); // 컬러 이미지의 경우
img.at<Vec3b>(y, x) = color;
}
}
return img;
}
Mat GetColorHistogram(Mat src) {
vector<Mat> bgr_planes;
split(src, bgr_planes);
int histSize = 256;
float range[] = { 0, 256 };
const float* histRange = { range };
bool uniform = true, accumulate = false;
Mat b_hist, g_hist, r_hist;
calcHist(&bgr_planes[0], 1, 0, Mat(), b_hist, 1, &histSize, &histRange, uniform, accumulate);
calcHist(&bgr_planes[1], 1, 0, Mat(), g_hist, 1, &histSize, &histRange, uniform, accumulate);
calcHist(&bgr_planes[2], 1, 0, Mat(), r_hist, 1, &histSize, &histRange, uniform, accumulate);
int hist_w = 512; // 히스토그램 이미지의 너비
int hist_h = 400; // 히스토그램 이미지의 높이
int bin_w = cvRound((double)hist_w / histSize);
Mat histImage(hist_h, hist_w, CV_8UC3, Scalar(0, 0, 0));
normalize(b_hist, b_hist, 0, histImage.rows, NORM_MINMAX, -1, Mat());
normalize(g_hist, g_hist, 0, histImage.rows, NORM_MINMAX, -1, Mat());
normalize(r_hist, r_hist, 0, histImage.rows, NORM_MINMAX, -1, Mat());
for (int i = 1; i < histSize; i++) {
line(histImage, Point(bin_w * (i - 1), hist_h - cvRound(b_hist.at<float>(i - 1))),
Point(bin_w * (i), hist_h - cvRound(b_hist.at<float>(i))),
Scalar(255, 0, 0), 2, 8, 0);
line(histImage, Point(bin_w * (i - 1), hist_h - cvRound(g_hist.at<float>(i - 1))),
Point(bin_w * (i), hist_h - cvRound(g_hist.at<float>(i))),
Scalar(0, 255, 0), 2, 8, 0);
line(histImage, Point(bin_w * (i - 1), hist_h - cvRound(r_hist.at<float>(i - 1))),
Point(bin_w * (i), hist_h - cvRound(r_hist.at<float>(i))),
Scalar(0, 0, 255), 2, 8, 0);
}
return histImage;
}
// 컬러 이미지에서 45도와 135도 에지 검출을 위한 소벨 필터 분리 및 통합
void mySobelFilter(const Mat& srcImg, Mat& dstImg45, Mat& dstImg135, Mat& dstImgCombined) {
int kernel45[3][3] = {
{-2, -1, 0},
{-1, 0, 1},
{0, 1, 2}
};
int kernel135[3][3] = {
{0, 1, 2},
{-1, 0, 1},
{-2, -1, 0}
};
dstImg45 = Mat(srcImg.size(), srcImg.type(), Scalar(0, 0, 0));
dstImg135 = Mat(srcImg.size(), srcImg.type(), Scalar(0, 0, 0));
dstImgCombined = Mat(srcImg.size(), srcImg.type(), Scalar(0, 0, 0));
const uchar* srcData = srcImg.data;
uchar* dstData45 = dstImg45.data;
uchar* dstData135 = dstImg135.data;
uchar* dstDataCombined = dstImgCombined.data;
for (int y = 0; y < srcImg.rows; y++) {
for (int x = 0; x < srcImg.cols; x++) {
for (int c = 0; c < 3; c++) { // 각 채널별로 처리
int sum45 = 0, sum135 = 0;
for (int j = -1; j <= 1; j++) {
for (int i = -1; i <= 1; i++) {
int newY = y + j;
int newX = x + i;
if (newY >= 0 && newY < srcImg.rows && newX >= 0 && newX < srcImg.cols) {
uchar val = srcData[(newY * srcImg.cols + newX) * 3 + c];
sum45 += val * kernel45[j + 1][i + 1];
sum135 += val * kernel135[j + 1][i + 1];
}
}
}
dstData45[(y * srcImg.cols + x) * 3 + c] = saturate_cast<uchar>(abs(sum45));
dstData135[(y * srcImg.cols + x) * 3 + c] = saturate_cast<uchar>(abs(sum135));
dstDataCombined[(y * srcImg.cols + x) * 3 + c] = saturate_cast<uchar>((abs(sum45) + abs(sum135)) / 2);
}
}
}
}
Mat mySampling(Mat srcImg) {
int width = srcImg.cols / 2;
int height = srcImg.rows / 2;
Mat dstImg(height, width, CV_8UC3);
// 가로 세로가 입력 영상의 절반인 영상을 먼저 생성
uchar* srcData = srcImg.data;
uchar* dstData = dstImg.data;
for (int y = 0; y < height; y++) {
for (int x = 0; x < width; x++)
{
// 각 B, G, R 값에 대해
dstData[y * width * 3 + x * 3] = srcData[(y * 2) * (width * 2) * 3 + (x * 2) * 3];
dstData[y * width * 3 + x * 3 + 1] = srcData[(y * 2) * (width * 2) * 3 + (x * 2) * 3 + 1];
dstData[y * width * 3 + x * 3 + 2] = srcData[(y * 2) * (width * 2) * 3 + (x * 2) * 3 + 2];
}
}
return dstImg;
}
vector<Mat> myGaussianPyramid(Mat src_img) {
vector<Mat> Vec;
Vec.push_back(src_img);
for (int i = 0; i < 4; i++) {
#if USE_OPENCV
pyrDown(src_img, src_img, Size(src_img.cols / 2, src_img.rows / 2));
#else
src_img = mySampling(src_img);
src_img = myGaussianFilter3x3(src_img);
#endif
Vec.push_back(src_img);
}
return Vec;
}
// 라플라시안 피라미드
vector<Mat> myLaplacianPyramid(Mat src_img) {
vector<Mat> Vec;
for (int i = 0; i < 4; i++) {
if (i != 3) {
Mat high_img = src_img;
#if USE_OPENCV
pyrDown(src_img, src_img, Size(src_img.cols / 2, src_img.rows / 2));
#else
src_img = mySampling(src_img);
src_img = myGaussianFilter3x3(src_img);
#endif
Mat low_img = src_img;
resize(low_img, low_img, high_img.size());
Mat laplacian = high_img - low_img + 128;
Vec.push_back(laplacian);
imshow("Laplacian Layer " + to_string(i), laplacian); // 각 레이어의 이미지를 표시
waitKey(0); // 사용자가 키를 누를 때까지 대기
}
else {
Vec.push_back(src_img);
imshow("Final Layer", src_img); // 마지막 레이어 이미지를 표시
waitKey(0); // 사용자가 키를 누를 때까지 대기
}
}
return Vec;
}
void gPyramid() {
cout << "--- GaussianPyramid ---\n" << endl;
Mat src_img = imread("gear.jpg", 1);
vector<Mat> vec_result = myGaussianPyramid(src_img);
imshow("0", vec_result[0]);
imshow("1", vec_result[1]);
imshow("2", vec_result[2]);
imshow("3", vec_result[3]);
imshow("4", vec_result[4]);
waitKey(0);
destroyAllWindows();
}
void LaPyramid() {
cout << "--- LaplacianPyramid ---\n" << endl;
Mat src_img = imread("gear.jpg", 1);
Mat dst_img;
vector<Mat> VecLap = myLaplacianPyramid(src_img);
reverse(VecLap.begin(), VecLap.end());
for (int i = 0; i < VecLap.size(); i++) {
if (i == 0) {
dst_img = VecLap[i];
}
else {
resize(dst_img, dst_img, VecLap[i].size());
dst_img = dst_img + VecLap[i] - 128;
}
string fname = "ex5_lap_pyr" + to_string(i) + ".png";
imwrite(fname, dst_img);
string windowName = "LaplacianPyramid" + to_string(i); // 각 창에 대해 고유한 이름 생성
imshow(windowName, dst_img); // 생성된 창 이름으로 이미지 표시
}
waitKey(0); // 사용자가 키를 누를 때까지 모든 창을 열어둠
destroyAllWindows(); // 모든 창 닫기
}
//각 함수 실행하는 main함수
int main() {
Mat srcImg = imread("gear.jpg", 1); // 이미지 로드
if (srcImg.empty()) {
cout << "Image not found!" << endl;
return -1;
}
// 1번
Mat filteredImg = myGaussianFilter9x9(srcImg);
Mat comparison;
hconcat(srcImg, filteredImg, comparison); // 원본과 필터링된 이미지 연결
imshow("Original vs Gaussian Filter", comparison);
waitKey(0);
// 2번
Mat histOriginal = GetColorHistogram(srcImg); //원본의 히스토그램
Mat histFiltered = GetColorHistogram(filteredImg); //필터링후의 히스토그램
imshow("Histogram - Original", histOriginal);
waitKey(0);
imshow("Histogram - Filtered", histFiltered);
waitKey(0);
// 3번
Mat noisyImg = addSaltPepperNoise(srcImg, 2000); //salt, pepper를 랜덤하게 2000개 찍기
Mat noiseFilteredImg = myGaussianFilter9x9(noisyImg); //디노이징
Mat noiseComparison;
hconcat(noisyImg, noiseFilteredImg, noiseComparison); // 노이즈 추가 이미지 및 디노이징 결과 이미지
imshow("Noise vs Denoised", noiseComparison);
waitKey(0);
// 4번
Mat sobelImg45, sobelImg135, sobelImgCombined;
mySobelFilter(srcImg, sobelImg45, sobelImg135, sobelImgCombined);
imshow("Sobel Filter 45 degrees", sobelImg45); //45도 필터만 적용한 이미지
waitKey(0);
imshow("Sobel Filter 135 degrees", sobelImg135); //135도 필터만 적용한 이미지
waitKey(0);
imshow("Sobel Filter Combined", sobelImgCombined); //45도, 135도 필터를 모두 적용한 이미지
waitKey(0);
// 5번
gPyramid();
// 6번
LaPyramid();
return 0;
}
1. 9x9 Gaussian Filter는 크기가 9x9인 가우스 커널을 사용하여 이미지를 스무딩하는 필터입니다. 이 필터는 이미지의 세부 노이즈를 줄이도록 설계되었습니다. 이전에 갖고 있던 ‘myGaussianFilter3x3’을 확장한 `myGaussianFilter9x9` 함수를 통해 각 픽셀에 대해 주변 픽셀의 가중 평균을 계산하여 적용합니다. `myGaussianFilter9x9` 함수에서 사용된 ‘myKernelConv9x9’도 ‘myKernelConv3x3’을 확장하여 만든 함수입니다. 결과적으로, 필터링된 이미지는 원본에 비해 노이즈가 감소했지만 조금은 뭉게진 모습을 볼 수 있습니다. 아래 결과 사진과 같이 영상을 원본 영상과 비교해 보면, 원본 대비 필터링된 영상에서 선명도가 감소하고 일반적인 이미지의 모양은 유지되나 부드러워진 것을 확인할 수 있습니다.
결과

2. 히스토그램은 이미지의 밝기 분포를 나타내는 그래프로, 필터링 전후의 히스토그램을 비교하여 필터의 효과를 분석할 수 있습니다. 위에서 사용한 함수는 기존 과제에서 제공되었던 컬러영상에 대한 히스토그램을 생성하는 함수입니다. 사용하도록 제시된 ‘gear.jpg’가 컬러 영상이기에 ‘GetColorHistogram’함수를 써야했습니다. 가우시안 필터를 적용한 후의 히스토그램을 보면, 고주파 성분의 제거로 인해 픽셀 값의 급격한 변화가 줄고, 이로 인해 히스토그램이 더 평활화된 형태로 나타납니다. 그래프의 우측부분에서 평활화 효과를 더 잘 확인할 수 있었는데 원래는 낮았던 부분들이 조금씩 높아진 것을 확인할 수 있고 가장 오른쪽에 높게 솟아있던 피크점이 확실히 줄어든 것을 확인한 수 있었습니다.
결과

3. ‘addSaltPepperNoise’함수를 통해 이미지에 흰색과 검은색의 점 노이즈를 무작위로 추가했습니다. 노이즈가 추가된 후, `myGaussianFilter9x9`를 적용함으로써 노이즈를 효과적으로 제거할 수 있었습니다. 필터 적용 후의 이미지는 노이즈가 크게 감소하였으며, 원본 이미지의 품질을 상당 부분 회복할 수 있었습니다. 이는 Gaussian Filter가 임의의 노이즈에 대해 강인하게 작동함을 보여줍니다. 물론 이전 과제를 통해서 median filter가 salt and pepper noise를 더 잘 처리한다는 것을 확인했었지만 9x9로 필터의 사이즈를 키우니 주변의 값으로 더 잘 매워져서 잘 작동한 것으로 예상됩니다.
결과

4. Sobel 필터는 이미지의 에지를 강조하기 위해 사용되는 기법으로, 특정 방향의 에지 강도를 강조합니다. 45도와 135도 각각의 에지를 감지하기 위해 서로 다른 커널을 사용합니다. `mySobelFilter` 함수를 통해 각 방향의 에지를 강조한 결과, 해당 방향의 에지가 선명하게 드러나며, 두 필터의 결과를 결합한 이미지는 두 방향의 에지가 모두 강조되어 전체적으로 에지가 잘 강조된 이미지를 제공합니다. 이는 방향성 에지 감지에 효과적인 필터링 방법을 보여줍니다.
결과

5. Gaussian Pyramid는 다양한 해상도의 이미지를 생성하여 다계층적으로 분석할 수 있게 해주는 기법입니다. `myGaussianPyramid` 함수를 사용하여 단계적으로 가우시안 필터를 적용하고 다운 샘플링을 하여 여러 단계의 해상도를 갖는 이미지 세트를 생성했습니다. 각 단계에서 이미지는 점점 작아지고 부드러워집니다.
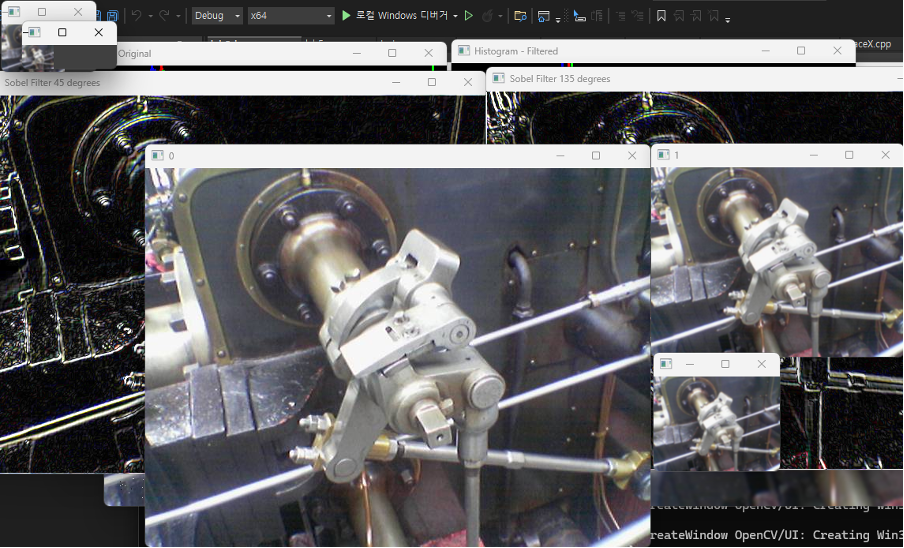


6. 라플라시안 피라미드는 이미지에서 세밀한 디테일을 강조하여 각 레이어를 생성합니다. `myLaplacianPyramid` 함수를 통해 구축된 피라미드는 각 단계에서 상세한 텍스처와 경계를 강조합니다. 라플라시안 피라미드는 가우시안 피라미드의 연속적인 레벨의 이미지간의 차이를 통해서 생성하는 구조이므로 함수에서 가우시안 피라미드 값을 참조하여 그 차이를 추출해내는 것을 볼 수 있습니다. 추가적으로 라플라시안 피라미드의 마지막 레벨 이미지는 차를 구할 가우시안 피라미드의 다음 레벨이 없기 때문에 가우시안 피라미드의 마지막 레벨의 이미지를 갖고와서 사용해야한다.



'Univ. Study > Digital Image Processing' 카테고리의 다른 글
| DIP 실습 - Segmentation / Clustering (0) | 2024.05.15 |
|---|---|
| DIP 실습 - Band pass filter / Frequency domain (0) | 2024.05.14 |
| Digital Image Processing - Clustering / Segmentation (0) | 2024.05.08 |
| Digital Image Processing - Color Image Processing (1) | 2024.05.01 |
| Digital Image Processing - Fourier transform / Frequency domain (0) | 2024.04.18 |



