Shell Sort
셸 정렬(Shell Sort)은 삽입 정렬을 개선한 버전으로, 1959년 도널드 셸(Donald Shell)에 의해 발표되었다. 삽입 정렬이 이웃하는 요소들과의 비교만을 수행하는 반면, 셸 정렬은 떨어진 요소들과의 비교를 통해 더 빠른 정렬을 가능하게 한다. Stable하고 In-place정렬법이라는 장점이 있다. 우선 정렬 과정을 직접 보자.


정렬과정에서 볼 수 있듯이 셸 정렬에서는 '간격(gap)'이라는 개념을 사용하여, 간격만큼 떨어진 요소들을 서로 비교하고 정렬한다. 초기 간격은 보통 배열 크기의 절반으로 설정하고, 각 단계마다 간격을 줄여나간다. 설정된 간격에 따라 배열을 여러 부분 리스트로 나누고, 각 부분 리스트에 대해 독립적으로 삽입 정렬을 수행한다. 간격을 줄여가며 위의 과정을 반복한다. 간격이 1이 될 때까지 이 과정을 반복한 뒤, 마지막으로 전체 배열에 대해 한 번 더 삽입 정렬을 수행한다. 알고리즘을 아래에서 살펴보자.
# Sort an array a[0...n-1].
gaps = [701, 301, 132, 57, 23, 10, 4, 1]
# Start with the largest gap and work down to a gap of 1
foreach (gap in gaps)
{
# Do a gapped insertion sort for this gap size.
# The first gap elements a [0..gap-1] are already in gapped order
# keep adding one more element until the entire array is gap sorted
for (i = gap; i < n; i += 1)
{
# add a[il to the elements that have been gap sorted
# save alil in temp and make a hole at position i
temp = a[i]
# shift earlier gap-sorted elements up until the correct location for a[il is found
for (j = i; j >= gap and a[j - gap] > temp; j -= gap)
{
a[j] = a[j - gap]
}
# put temp (the original a[il) in its correct location
a[j] = temp
}
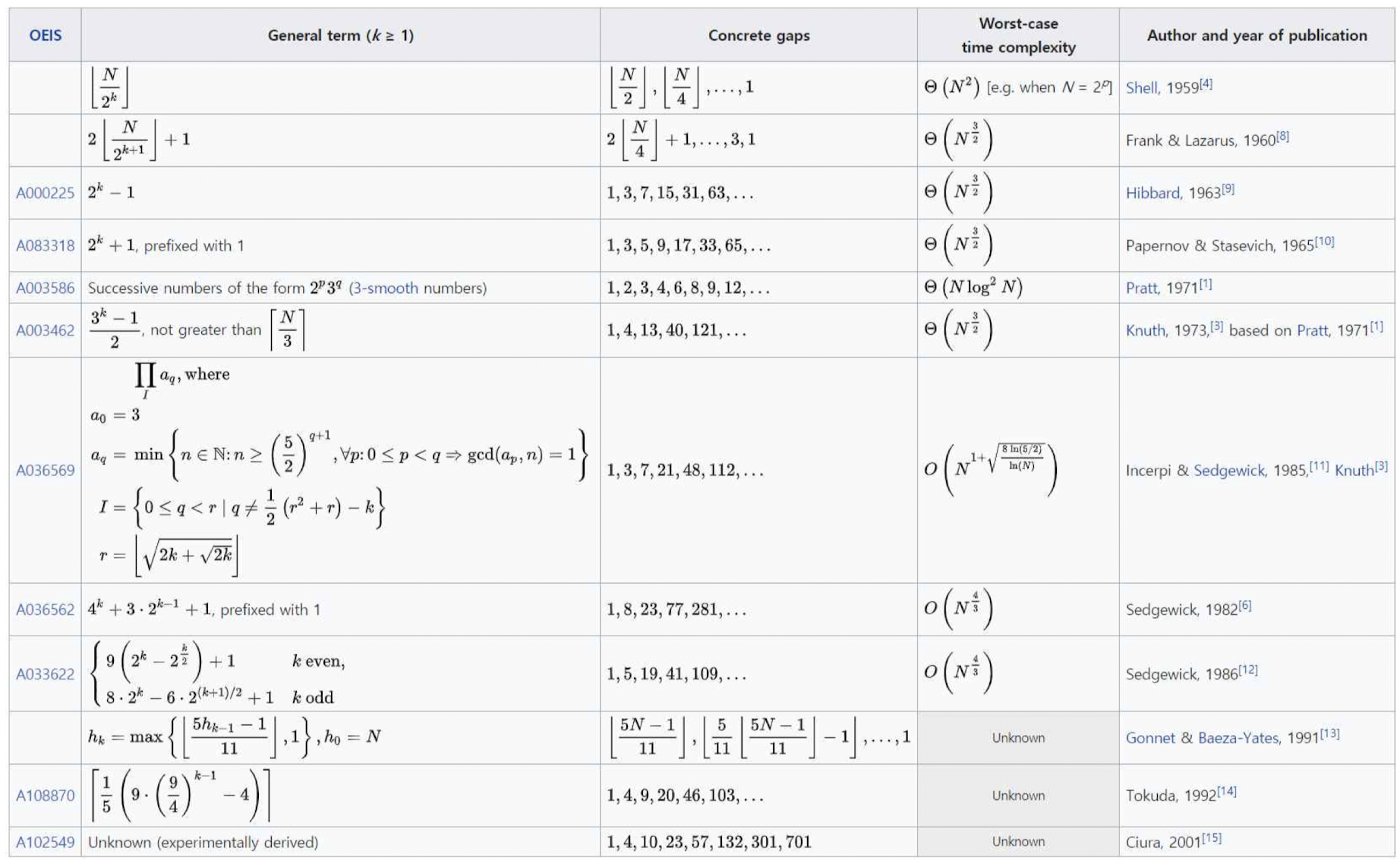
}셸 정렬에서 주의해야할 점은 갭으로 선정되는 수열에 따라 그 성능이 크게 바뀐다는 점이다. 셸이 제시한 수열은 절반으로 줄어드는 단순한 수열이지만 추후 많은 연구를 통해 time-complexity를 줄이려는 시도가 많이 진행되었다.
Quick Sort
퀵 정렬은 이전에도 다뤘었으니 퀵 정렬의 성능을 개선하는 방법에 대해서 살펴보자. 크게 3가지 정도가 있다.
1. 스택을 사용하여 순환을 제거
2. 작은 부분화일의 경우 삽입 정렬 사용
3. 중간값 분할(Median-of-Three Partitioning)
아래는 스택을 사용하여 순환을 줄인 알고리즘을 구현한 것이다.
void QuickSort(int a[], int l, int r) {
int i, j, v;
for ( ; ; ) {
while (r > l) {
i = partition(a, l, r);
if (i-l > r-i) {
push(&top, l); push(&top, i-1); l = i+1;
}
else {
push(&top, i+1); push(&top, r); r = i-1;
}
}
if (top < 0) break;
r = pop(&top); l = pop(&top);
}
}
다음은 부분화일 크기가 일정수준 이하로 내려가면 삽입정렬을 사용하도록하는 알고리즘을 구현한 것이다.
void QuickSort(int a[], int l, int r)
{
int i, j, v;
if (r-l <= M) InsertionSort(a, l, r); //M은 5~25정도로 설정되는 작은 부분 화일의 기준이다.
else {
v = a[r]; i = l-1; j = r;
for ( ; ; ) {
while (a[++i] < v);
while (a[--j] > v);
if (i >= j) break;
swap(a, i, j);
}
swap(a, i, r);
QuickSort(a, l, i-1);
QuickSort(a, i+1, r);
}
}
중간 값 분할이란 분할 원소를 선택할 때 왼쪽, 가운데, 오른쪽 원소 중 값이 중간인 원소를 선택하는 것이다. 왼쪽, 가운데, 오른쪽 원소를 정렬한 후 가장 작은 값을 a[l], 가장 큰 값을 a[r], 중간 값을 a[r-1]에 넣고, a[l+1], ..., a[r-2]에 대해 분할 알고리즘을 수행한다. 장점은 최악의 경우가 발생하는 확률을 낮추어 주고 경계 키(sentinel key)를 사용할 필요가 없다는 것이다. 결정적으로 전체 수행 시간을 약 5% 감소시킨다. 해당 알고리즘을 구현하면 아래와 같다.
void QuickSort(int a[], int l, int r)
{
int i, j, m, v;
if (r - l > 1) {
m = (l + r) / 2;
if (a[l] > a[m]) swap(a, l, m);
if (a[l] > a[r]) swap(a, l, r);
if (a[m] > a[r]) swap(a, m, r);
swap(a, m, r-1);
v = a[r-1]; i = l; j = r-1;
for ( ; ; ) {
while (a[++i] < v);
while (a[--j] > v);
if (i >= j) break;
swap(a, i, j);
}
swap(a, i, r-1);
QuickSort(a, l, i-1);
QuickSort(a, i+1, r);
}
else if (a[l] > a[r]) swap(a, l, r);
}
추가로 k번째 숫자를 찾는 task에 대해서도 퀵정렬은 강력하다. pivot을 swap하면 해당 pivot의 순서는 이후의 연산과 관계없이 결정되는 것이기 때문에 정렬을 모두 기다리고 다시 k번째까지 카운팅을 하지 않고 k번째 숫자와 pivot이 swap되는 순간 결과를 출력하면 빠르게 k번째 숫자를 찾을 수 있다.
Heap Sort
우선 순위 큐의 일종인 힙(heap)을 이용해 정렬한다.
작동과정을 살펴보면 정렬할 원소를 모두 공백 힙에 하나씩 삽입하고 제일 큰 원소를 하나씩 삭제한다. 삭제된 원소들은 순서대로 리스트에 삽입하여 자동으로 정렬된 결과가 나온다.

힙은 위와 같이 정렬이 된다. 1번 인덱스의 숫자를 pop 시키고 다시 정렬하고 pop 시키고를 반복하는 것이다. 해당 알고리즘은 아래와 같이 구현된다.
HeapSort(a[])
n←a.length-1; //n은히프크기(원소의수)
// a[0]은 사용하지 않고 a[1 : n]의 원소를 오름차순으로 정렬
for (i ← n/2; i ≥ 1; i ← i-1) do // 배열 a[]를 히프로 변환
heapify(a, i, n); // i는 내부 노드
for (i ← n-1; i ≥ 1; i ← i-1) do { //배열 a[]를 오름차순으로 정렬
temp ← a[1]; // a[1]은 제일 큰 원소
a[1] ← a[i+1]; // a[1]과 a[i+1]을 교환
a[i+1] ← temp;
heapify(a, 1, i);
}
end heapSort()heapify함수 구현법까지 살펴보면 아래와 같다.
heapify(a[], h, m)
// 루트 h를 제외한 h의 왼쪽 서브트리와 오른쪽 서브트리는 히프
// 현재 시점으로 노드의 최대 레벨 순서 번호는 m
v ← a[h];
for (j ← 2*h; j ≤ m; j ← 2*j) do {
if (j < m and a[j] < a[j+1]) then j ← j+1;
// j는 값이 큰 왼쪽 또는 오른쪽 자식 노드
if (v ≥ a[j]) then exit;
else a[j/2] ← a[j]; // a[j]를 부모 노드로 이동
}
a[j/2] ← v;
end heapify()
우측의 표순서대로 가장 큰 수부터 정렬이 되는 것을 볼 수 있다. 그 과정을 트리구조로 살펴보면 아래와 같다.

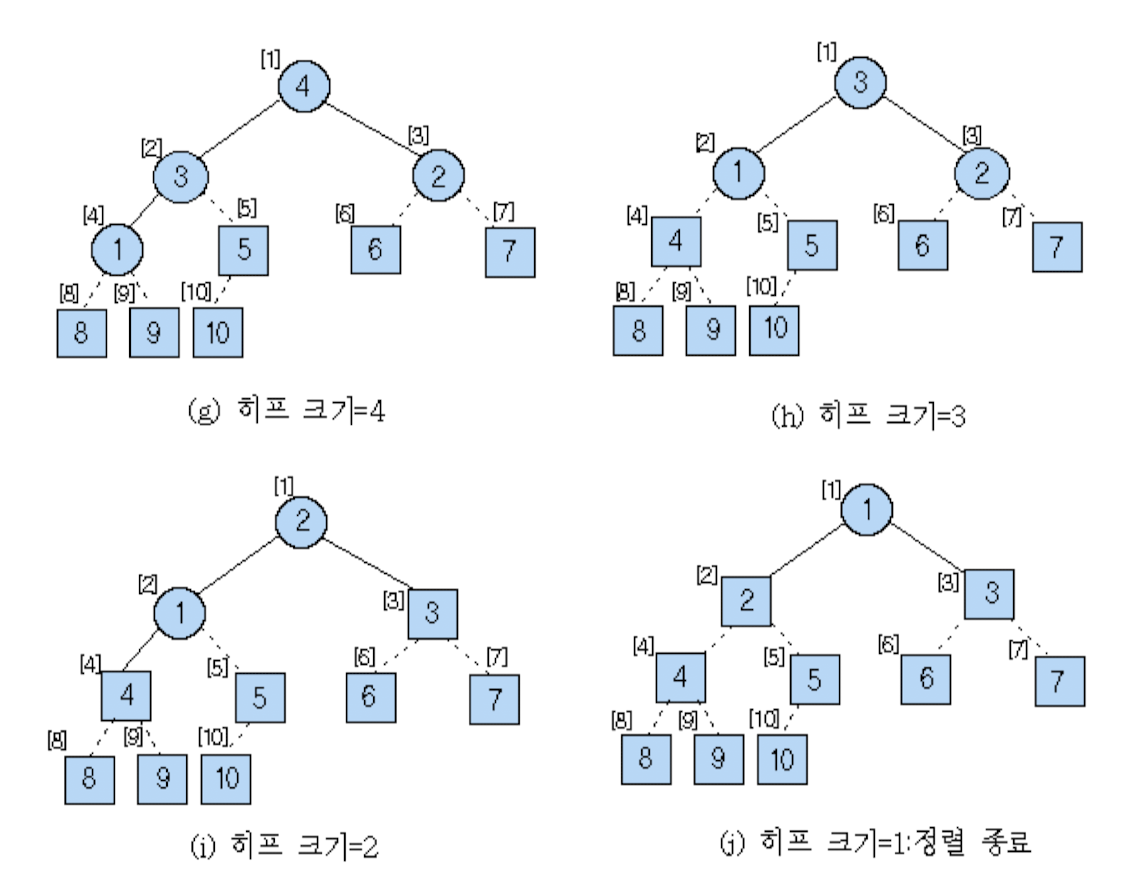
In-place정렬이지만 unstable하다는 특징이 있다.
Counting Sort
계수 정렬은 입력키가 어떤 범위에 있을때 적용이 가능하다. 예를들어 1부터 k사이의 작은 정수 범위에 있다는 것을 미리 알고 있을 때에만 적용이 가능한것이다. 수행과정을 표로 살펴보면 아래와 같다.
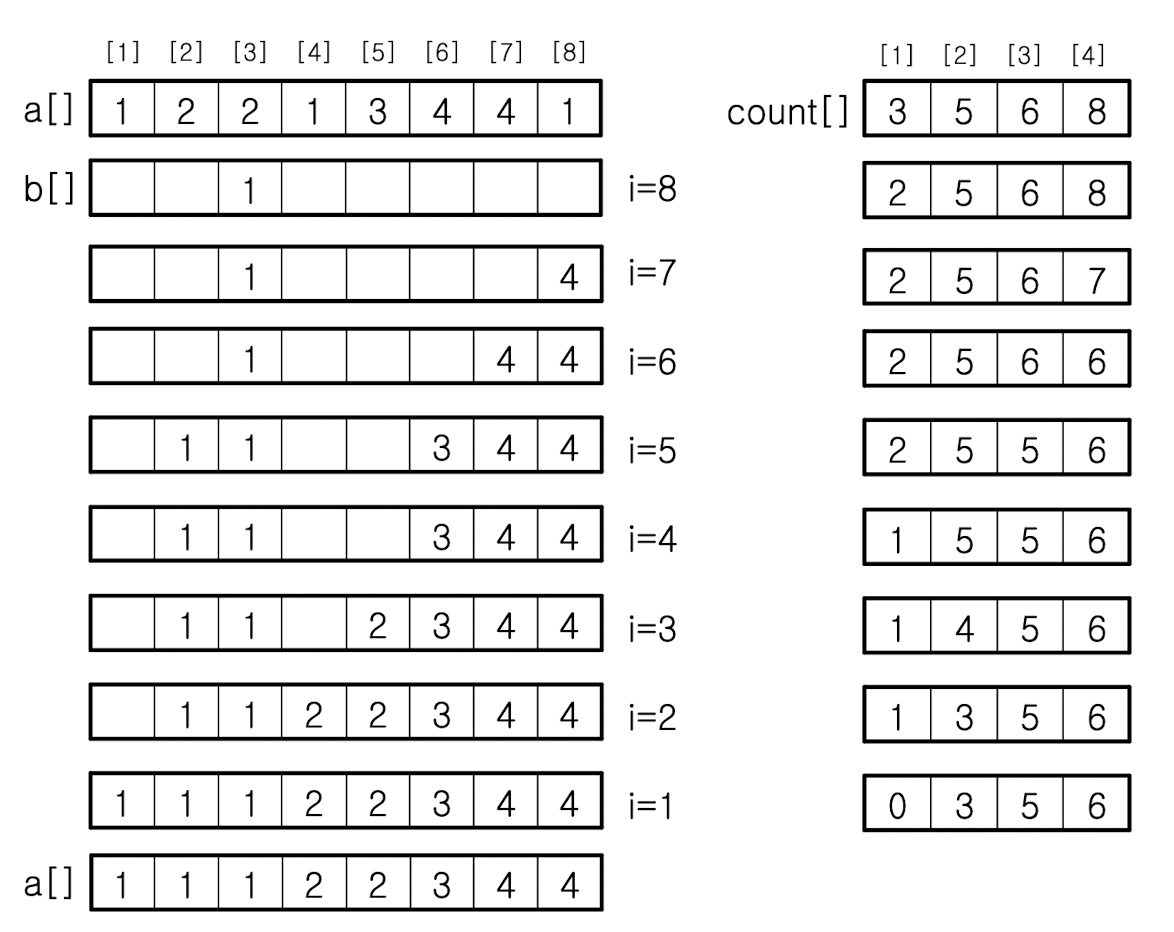
알고리즘은 아래와 같이 구현된다.
CountingSort(a[], n, m)
for (j←1; j≤m; j←j+1) do count[j]←0; //count[]를 0으로 초기화
for (i ← 1; i ≤ n; i ← i + 1) do count[a[i]] ← count[a[i]] + 1;
// 원소의 개수를 세어 count[]에 저장
for (j ← 2; j ≤ m; j ← j + 1) do count[j] ← count[j-1] + count[j];
// 원소가 들어 갈 위치 계산
for (i ← N; i ≥ 1; i ← i - 1) do {
b[count[a[i]]] ← a[i]; // a[]의 원소를 b[]의 미리 계산된 위치로 이동
count[a[i]] ← count[a[i]] - 1; // count[]의 값을 하나 감소시킴
}
for (i ← 1; i ≤ n; i ← i + 1) do a[i] ← b[i]; // b[]를 a[]로 이동
end CountingSort()Nested for loop가 없어서 시간복잡도는 특정 조건에서 O(N)이지만 실제로 매번 그런 이상적인 결과가 나오지는 않는다. 그럼에도 비교기반의 정렬들에 비해서 속도가 빠른것은 사실이다.
Stable하고 In-place정렬은 아니다.
Radix Sort
기수 정렬은 전체 키를 여러 자리로 나누어 각 자리마다 계수 정렬과 같은 안정적 정렬 알고리즘을 적용하여 정렬하는 방법이다. d 자리수 숫자들에 대하여 계수 정렬로 정렬하는 것이다. 각 자리수마다 O(N) 시간이 걸리므로 전체로는 O(dN) 시간이 걸리는데, d를 상수로 취급할 수 있다면 O(N) 시간이 걸리게 된다. 전체 정렬 데이터 개수만큼의 기억 장소와 진법 크기만큼의 기억 장소가 추가로 필요하다는 단점은 존재한다. 수행과정을 그림을 통해 살펴보자.

알고리즘은 아래와 같이 구현된다.
RadixSort(a[], n)
for(k←1;k≤m;k←k+1)do{ //m은digit수,k=1은가장작은자리수
for (i ← 0; i < n; i ← i+1) do {
kd ← digit(a[i], k); // k번째 숫자를 kd에 반환
enqueue(Q[kd], a[i]); // Q[kd]에 a[i]를 삽입
}
p ← 0;
for (i ← 0; i ≤ 9; i ← i+1) do {
while (Q[i] ≠ Ø) do { // Q[i]의 모든 원소를 a[]로 이동
p ← p+1;
a[p] ← dequeue(Q[i]);
}
}
}
end RadixSort()'Univ. Study > Algorithm Design' 카테고리의 다른 글
| 알고리즘 설계 실습 - k번째 교환(heap sort) (0) | 2024.03.30 |
|---|---|
| Algorithm Design - Parallel Sorting Algorithm / 바이토닉 정렬 / 홀짝 정렬 (1) | 2024.03.26 |
| 알고리즘 설계 실습 - 두 정삼각형 (1) | 2024.03.21 |
| Algorithm Design - Master Theorem (0) | 2024.03.14 |
| Algorithm Design - 실습(GDC_LCM, Sort) (0) | 2024.03.13 |



