Big O
Big O notation으로 어떻게 표현되는 알고리즘이느냐에 따라 아예 수행이 불가능한 알고리즘이 될 수도 있다.

점근적 상한(Asymptotic Upper Bound) 방법을 이용하여 정의되고 표현한다. 주어진 복잡도 함수 f(n)에 대해서 g(n)∈O(f(n)) 이면 다음을 만족한다.
n≥N인 모든 정수n에 대해서 g(n) ≤ c x f(n)이 성립하는 실수 c>0와 음이 아닌 정수 N이 존재한다.
이는 아래와 같이 그래프를 통해 살펴볼 수 있다.

어떤 함수 g(n)이O(n^2)에 속한다는 말은 그 함수는 어떤 임의의 N값보다 큰 값에 대해서는 어떤 2차함수 cn^2 보다는 작은 값을 가지게 된다는 것을 뜻한다. (그래프 상에서는 아래에 위치)
반대로 어떤 알고리즘의 시간복잡도가 O(f(n))이라면 입력의 크기 n에 대해서 이 알고리즘의 수행시간은 아무리 늦어도 f(n)은 된다. 다시 말하면, 이 알고리즘의 수행시간은 f(n)보다 절대로 더 느릴 수는 없다는 말이다.
“길어야 N 시간이면 된다”가 사실이라면 당연히 “길어야 N^2 시간이면 된다”라거나 “길어야 N^3 시간이면 된다”도 사실이다. 이때 알고리즘의 특성을 표현하는 데는 tight upper bound를 사용해야 함. “2n is O(n)” 대신 “2n is O(n^2)”이라고 표현해야하는 것이다.
Example
n^2 + 10n이 O(n^2)인지를 증명하려면 아래와 같이 여러 방법이 있다.
(1) n≥10인 모든 정수 n에 대해서 n2+10n ≤ 2n^2 이 성립한다. 그러므로,c=2 와 N = 10을 선택하면, “Big O”의 정의에 의해서 n^2+10n∈O(n^2)이라고 결론 지을 수 있다.
(2) n≥1인 모든 정수 n에 대해서 n^2+10n ≤ n^2+10n^2=11n^2 이성립한다.그러 므로, c = 11와 N = 1을 선택하면, “Big O”의 정의에 의해서 n2+10n ∈ O(n2) 이라고 결론지을 수 있다.
첫번째 경우를 그래프로 표현하면 아래와 같다.

N=10 이후로 파란색 그래프인 2n^2가 더 빠르게 상승하여 Upper bound 역할이 됨을 볼 수 있다.
Big Ω
이는 Big O와 반대로 점근적 하한(Asymptotic Lower Bound)을 찾는 방식이다. 주어진 복잡도 함수 f(n)에 대해서 g(n)∈Ω(f(n)이면 다음을 만족한다.
n≥N인 모든 정수 n에 대해서 g(n)≥c x f(n)이 성립하는 실수 c>0와 음이 아닌 정수 N이 존재한다.

간단한 예시를 살펴보고 마치자.
n^2 +10n∈Ω(n2)을 증명하라
n≥30인 모든 정수 n에 대해서 n^2+10n ≥ n^2 이 성립한다. 그러므로, c = 1와 N = 0을 선택하면, n^2 +10n ∈Ω(n^2)이라고 결론지을 수 있다.
Big Θ
어떤 알고리즘이 O(n^2)임을 증명하면 “길어야 이만한 시간이면 된다”라는 뜻이고 Ω(n)임을 증명하면 “최소한 이만한 시간은 걸린다”라는 뜻이된다. 반면 Big Θ는 둘의 사이에 존재하는 최선의 알고리즘을 뜻한다.
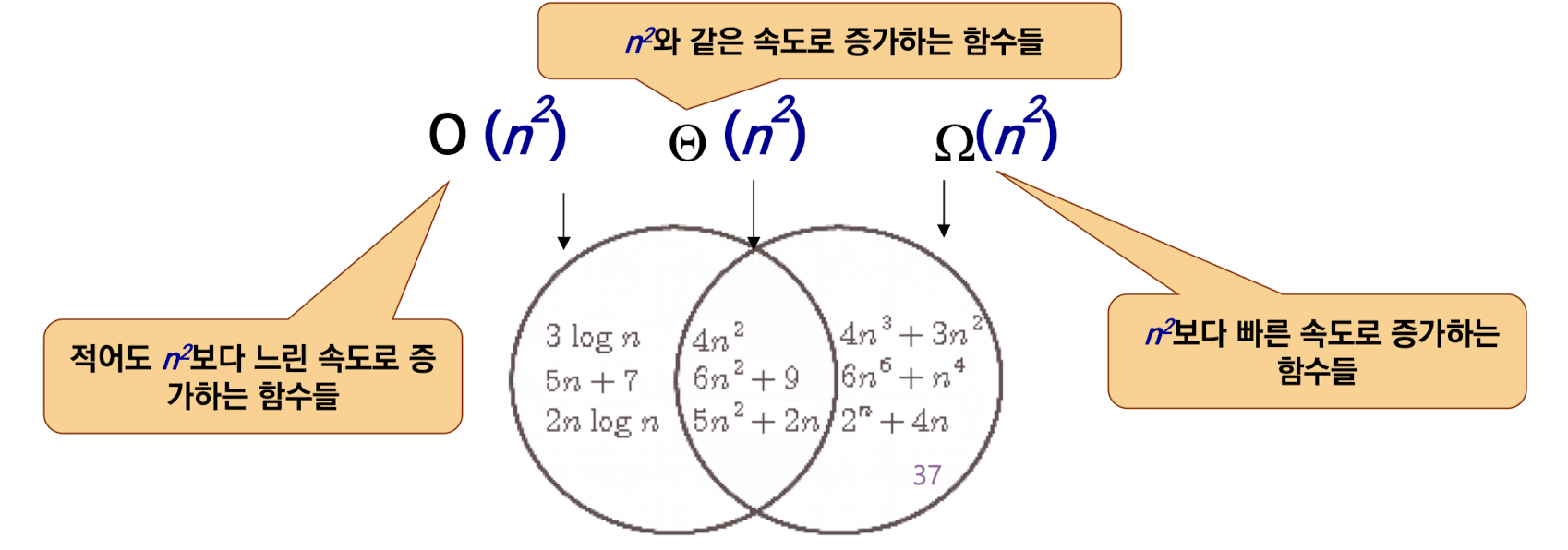
상한과 하한이 마주 침으로써 더 이상 나은 알고리즘은 존재하지 않는 것이다. order(차수)의 엄밀하고 정확한 정의이다.
그래프로 보면 아래와 같이 묘사할 수 있다.

Recursion
재귀란 함수가 자기 자신을 호출하여 문제를 해결하는 프로그래밍 기법을 말한다.
재귀는 크게 두 가지 요소로 구성된다.
기저 조건(Base Case): 함수가 더 이상 자기 자신을 호출하지 않고 결과를 직접 반환하는 경우로 재귀가 끝나는 지점이다.
재귀 단계(Recursive Case): 현재 문제를 더 작은 문제로 분할하여 자기 자신을 다시 호출하는 단계이다.
재귀 함수를 사용하는 대표적인 예로는 분할 정복(divide and conquer) 알고리즘이 있다. 이는 복잡한 문제를 더 작고 다루기 쉬운 부분 문제로 나누어 해결하고, 이렇게 분할된 문제들의 해결 결과를 결합하여 원래 문제의 해결을 도모하는 방식이다.
재귀 함수의 설계 원칙에는 다음과 같은 것들이 있다.
if simplest case then solve directly;
else make a recursive call to a simpler case;
이 원칙들을 통해 재귀 함수는 문제를 해결할 수 있다. 재귀는 명확하고 이해하기 쉬운 해결책을 제시할 수 있지만, 무한 재귀 또는 스택 오버플로우와 같은 문제에 주의해야 한다.
Example
Binary Search는 주어진 탐색키 key가 저장된 위치(인덱스) 찾아내는 알고리즘으로 아래의 과정으로 통해 진행된다.
• key = a[mid] : 탐색 성공, return mid
• key < a[mid] : a[mid]의 왼편에 대해 탐색 시작
• key > a[mid] : a[mid]의 오른편에 대해 탐색 시작
BinarySearch(a[], key, left, right)
// a[mid] = key인 경우 mid를 반환
if (left <= right) then
mid <- (left + right) / 2;
case {
key = a[mid] : return (mid);
key < a[mid] : return (BinarySearch(a, key, left, mid-1));
key > a[mid] : return (BinarySearch(a, key, mid+1, right));
}
else return -1; // key 없이 검색하면 -1 반환
end BinarySearch()
아래는 Divide and Conquer 방법을 사용하는 대표적인 sorting 알고리즘인 mergesort이다.
void mergesort(int n, keytype S[]) {
const int h = n / 2, m = n - h;
keytype U[1..h], V[1..m];
if (n > 1) {
copy S[1] through S[h] to U[1] through U[h];
copy S[h+1] through S[n] to V[1] through V[m];
mergesort(h, U);
mergesort(m, V);
merge(h, m, U, V, S);
}
}순환 알고리즘 점화식
Tn = Tn-1 + N => Tn = O(N^2) case

Tn = 2Tn/2 + N => Tn = O(NlogN) case

Tn = Tn/2 + N => Tn = O(N) case

Tn = 2Tn/2 + 1 => Tn = O(N) case

Tn = Tn/2 + 1 => Tn = O(logN) case

'Univ. Study > Algorithm Design' 카테고리의 다른 글
| Algorithm Design - Master Theorem (0) | 2024.03.14 |
|---|---|
| Algorithm Design - 실습(GDC_LCM, Sort) (0) | 2024.03.13 |
| Algorithm Design - Intro/Data structure (0) | 2024.03.09 |
| Lecture 16 - 강연결 요소 + 그리디 알고리즘(1) (0) | 2023.05.15 |
| Lecture 18 - Graph(2) (2) | 2023.05.08 |



